If the brain is in fact capable of generating rich and complex volumetric moving images, and if those images are indeed defined by spatial standing waves in the brain, the potential for future research of this new principle of neurocomputation is literally unlimited. In fact, this would open up a whole new field of investigation with branches into many interesting directions, some of which are summarized below.
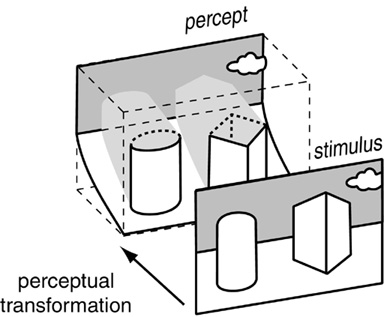
One direction of research would be to continue the quantitative modeling of perceptual experience, that is, to devise spatial computational algorithms that perform the perceptual transformation depicted below, expanding a two-dimensional stimulus into a three-dimensional volumetric percept, using a three-dimensional directed diffusion and three-dimensional directional harmonic vertices as described in Lehar (2003a, 2003b).

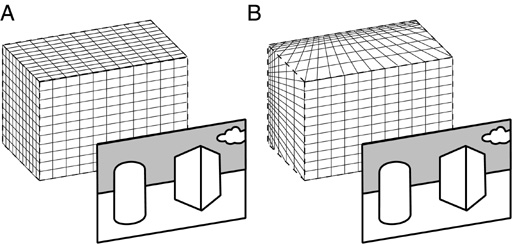
We begin with a volumetric "voxel" data structure, like those used in MRI and CAT images, to define the space of perceptual experiene, as shown in A below left. To mimic phenomenal perspective the scale of the representation is made to vary in nonlinear fashion, as suggested in B below right.
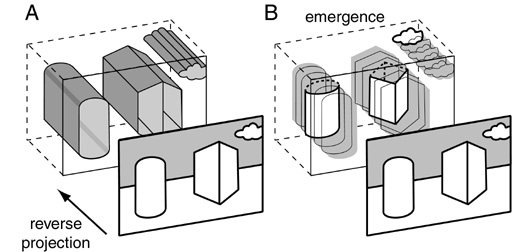
The two-dimensional stimulus is then reverse-projected into the volumetric representation as suggested in A below, expressing the locus of every possible spatial interpretation of the given stimulus. The final percept then emerges from this superposition of states by a dynamic relaxation process whose minimal energy state corresponds to the final perceptual interpretation, as suggested in B below (Lehar 2003a, 2003b).
The simulation of the emergent processes in perception is very computational-intensive, because like the neural network model, the computer simulation of spatial perception requires a three-dimensional spatial convolution with spatial templates of every possible configuration at every spatial location and every orientation, with a simplicity measure for every perceptual interpretation to allow selection of the simplest one. In a parallel analog spatial algorithm however, like a harmonic resonance process, this computation can occur virtually instantaneously and in parallel. (Lehar 2003a)
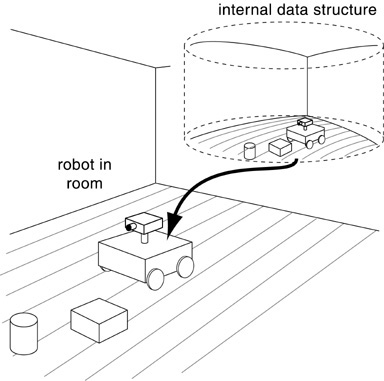
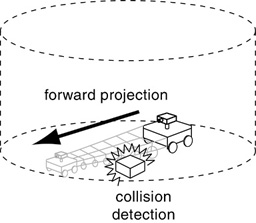
For example a desire to move in a certain direction can be expressed as a spatial projection function that projects the robot's body-image forward in perceptual space, as suggested below, like a series of frames from a movie, each time-stamped for one instant further into the future than the last, projected into forward space and future time. This is the reified rendition of the motor act, constructed, or filled-in, as volumes moving through space and time. This forward projection allows the detection of potential collisions with objects by marking volumetric regions that are occupied by more than one object, as shown below, as in a ray-tracing algorithm.
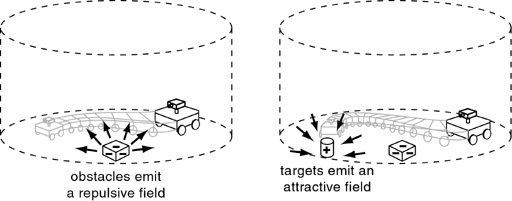
Potential obstacles should also project spatial fields of influence that act on the forward projection to distort its form. To avoid collisions, obstacles are marked with a repulsive field that eminates outward in all directions, repelling the forward-projected path away from it, as suggested below left. Objects recognized as targets are marked with an attractive field that draws the end of the forward-projected path of the robot toward itself, as suggested below right.
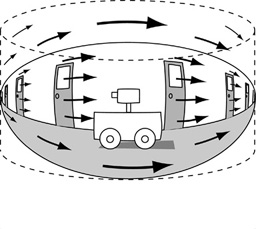
The forward projection drifts about like an elephant trunk, until it finds an optimal configuration for the given environment. The projected motion can then be executed at any time by simply following the projected path, frame by frame. As the robot moves forward through the world, the internal model of the world is translated backward coherently, as another parallel spatial computation, with the robot's body-image fixed at the center as the world scrolls by.
Although it is difficult to imagine how this kind of spatial computation might be performed in the brain, it is easy to see how useful this computation function would be for practical interaction with the world, as well as for a plausible account for the observed spatial structure of experience. The problem of robotic navigation is far from solved, as the DARPA "Grand Challenge" desert road race painfully reveals, and therefore novel and unconventional approaches to spatial perception must be given serious consideration. The concept of spatial computations in a spatial medium is a unique computational strategy which has never been tried for robot navigation. Its intensive spatial computations are just reaching the brink of feasability in today's computational hardware. Furthermore, phenomenological examination clearly reveals that this is the way that the brain addresses the navigation problem, so this approach deserves at least to be given a try.
The parallel analogical principle of perceptual computation is inherently inefficient when expressed in a Boolean sequential algorithm on a digital computer, so computer simulations of analogical spatial logic can offer insights into the spatial algorithms used in the brain, but in order for those computations to be at all practical, they must ultimately be expressed in the same parallel analogical manner as it is computed in the brain. I propose that analogical principle behind spatial reification in the brain is harmonic resonance.
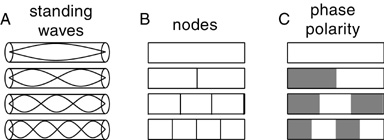
If standing waves are indeed used to project spatial images in the brain, then surely the same principle would be useful as a spatial representation in an artificial intelligence designed to operate on the same essential principles as the brain. Standing waves define sinusoidal patterns of alternating compression and rarefaction. In a linear arrangement like a flute, the standing waves subdivide the flute into integer numbers of equal intervals, as shown in A below, for the first four harmonics of the depicted flute. Figure B below shows the pattern of nodes of the standing waves, while figure C below shows the polarity of the phase of the standing wave, a regular alternating pattern of polarity.
In a two-dimensional resonating system there are many more possible standing wave patterns, as demonstrated by the Chladni figures, produced by bowing a steel plate with a violin bow to make it ring like a bell, as shown in figure A below, with sand sprinkled on the plate to reveal the pattern of nodes for each standing wave resonance. Figure B below shows some of the many patterns of standing waves for a square steel plate.
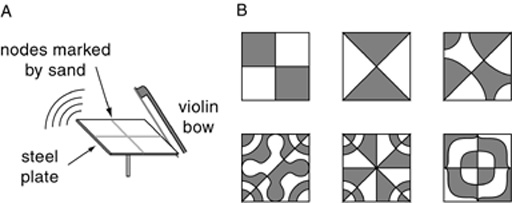
The next figure below shows an array of nodal patterns for a square steel plate found by Waller (1962). Every one of these distinct patterns of standing waves has a distinct frequency of oscillation, or musical tone.

The various standing wave patterns on a Chladni plate can therefore be identified or recognized by a bank of tuned resonators, each one tuned to one of the various harmonics of the steel plate. Each resonator will vibrate in sympathy with the resonance on the plate whenever the pattern on the plate matches the characteristic frequency of that resonator. The resonator thus acts as a feature detector, that recognizes the presence of its particular standing wave on the vibrating plate. But the resonator does more than just recognition, because by resonating at its characteristic frequency, it automatically generates a copy of its characteristic standing wave back on the vibrating steel plate. In other words the resonator automatically reifies a spatial image of its characteristic pattern as a standing wave on the vibrating steel plate, whenever it is activated. This principle of top-down reification of a spatial pattern is a unique and significant property of harmonic resonance.
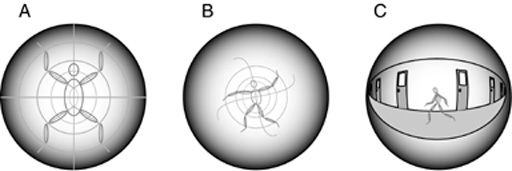
Standing waves can also be sustained in three-dimensional volumetric resonators, like the resonating sphere depicted in A below, where the standing waves will tend to subdivide the spherical cavity into integer numbers of equal intervals of alternating phase in patterns of longitude, lattitude, and concentric shells. Figure B below depicts some of the infinite patterns of standing waves in a spherical resonator, showing lattitudinal rings, longitudinal slices, and a compound checkerboard pattern, each of which has a characteristic vibration frequency and waveform.

A significant feature of a circular or spherical resonator is that the standing waves that emerge within it are free to rotate to any orientation while maintaining the same frequency and waveform, and thus the resonator tuned to that frequency performs a rotation-invariant recognition of spatial form, although the pattern of standing waves in the resonator does have a specific orientation at any moment in time. This is the kind of mechanism required to account for rotation invariance in the recognition of simple objects in perception.
Fourier theory shows that virtually any pattern can be constructed out of component sinusoids. A standing wave representation can therefore represent virtually any pattern as a compound standing wave with higher harmonics. For example just the right waveform of driving resonance would produce the standing wave shown below left, designed to mimic the configuration of the human body to some level of accuracy. The standing wave can be morphed or modulated into different postures, as suggested in B below, and it can be made to cycle endlessly through a cyclic pattern of motion like walking or running motions. This standing wave body-image can thus serve as a volumetric template to represent either the present posture of the body, as measured proprioceptively, or the intended posture at some future time for motor planning.
A standing-wave image of a surrounding environment, can now be added around the body-image homunculus, as suggested in C above, and the standing wave homunculus can now begin to respond to the spatial configuration of its perceived environment by way of spatial motions of its standing wave limbs, which are then replicated by the motion of its real limbs. In a linear resonating system different waves pass through each other without any effect on each other. In a nonlinear resonator on the other hand, passing waves do influence or modulate each other. An interesting direction of research would be to investigate how the pattern of one standing wave can serve to transform or modulate the pattern of another, and to devise mechanisms for controllably morphing standing waves in lawful manner. For example a projection of the body-image forward into space can be accomplished by simply allowing higher harmonics of resonance to emerge from the fundamental standing wave representing the body in the direction of the projection, to produce a periodic array of body-images, as suggested below, like the reflections between facing mirrors.

The resonance mechanism proposed above is highly speculative, and would require a good deal of research to determine exactly which aspects of it are feasable. We do know however that standing waves represent a unique and largely unexplored principle of spatial representation and reification, which can in principle express virtually any pattern in space and time, and therefore, harmonic resonance offers the only plausible hypothesis proposed to date to account for the profound spatial problem in visual representation.
A conservative research plan would be to investigate the types of patterns possible in simple resonating systems constructed of ripple tanks, vibrational and acoustical systems, electronic oscillator circuits, amplified electrical instruments, and laser and maser principles using advanced electro-optic components. In all of these many and various methods of resonance, the objective would be to define spatial patterns by controlling the driving resonances, in order to explore the range of possible patterns that can be generated by manipulation of higher harmonics. This will reveal the natural grammar that expresses those patterns in the harmonic resonance code, and thus will reveal the natural grammar behind spatial perception in biological vision.
The potential for the principle of spatial representation by harmonic resonance in real-world commercial applications is literally boundless. For example standing waves could be used to define the spatial pattern of the printed circuit on a semiconductor chip by subjecting the chip to vibrational resonances across its x and y dimensions using piezo-electric transducers driven by the waveform devised to represent the spatial pattern of the intended circuit, as suggested below.
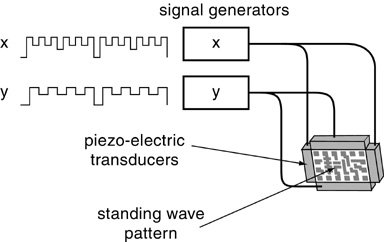
All that is required is some means by which the doping of the semiconductor is made to occur in the pattern defined by the phase of the standing wave, in order to imprint that transient pattern of the standing wave as a permanent mark on the chip. Similarly, standing waves might be used in printing applications where the standing wave on a vibrating chip determines the pattern of ink printed on the page. Standing waves could also be used as a means of projecting an image on a screen, by making the color and brightness of each point on the screen correspond to the phase of the standing wave across the screen, or by passing coherent light through an electro-optic modulator driven by a standing wave resonance, as suggested below.
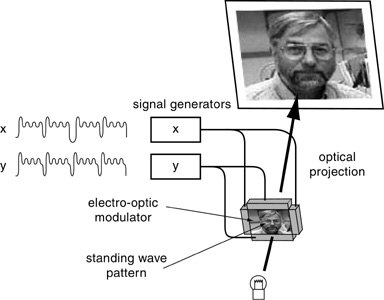
The advantage of using harmonic resonance for representing spatial imagery is that it naturally offers a global means to control the image, in the manner of Fourier filtering operations, because a standing wave representation essentially performs a Fourier transform on a spatial image and expresses its harmonic content in the form of an array of pitches, or musical tones, one for each harmonic component of the spatial standing wave, all playing together harmoniously like a great chord on a cathedral organ. Manipulating the frequency content of this chord by amplifying or suppressing individual components will modulate the corresponding standing wave pattern as a whole in a global Gestalt manner, as in Fourier filtering operations. All of these are potentially patentable applications with great potential for commercial and theoretical significance, and they all stem from the single insight of employing standing waves as a representation of spatial pattern, inspired by biological vision.
If the spatial structure of experience is encoded in spatial standing waves in the brain, it must be possible to detect those spatial structures in the brain neurophysiologically, another promising direction of investigation. I propose that standing waves have already been detected in the cortex, in the form of synchronous oscillations between neurons which are responding to different parts of the same perceived object. According to the harmonic resonance theory, the phase of oscillation is not a signal in its own right transmitted from one cell to the other, but rather, the synchrony is a local manifestation of a global standing wave resonance that unites the percept into a single integrated whole. A standing wave model would predict that the phase of the oscillation of cortical neurons should be observed to vary periodically along the spatial extent of the standing wave as it is sampled at different cortical locations, and that pattern of phase corresponds to the configuration of the perceptual experience in an analogical, or map-like manner. This prediction could be easily tested. A standing wave theory would predict that viewing a sinusoidal grating should set up a standing wave across the visual cortex whose phase matches the dark/light reversals of the grating itself. Shifting the grating laterally should result in a shift of the phase of the standing wave. These predictions could be easily tested in experimental animals.
The harmonic resonance theory finally offers an explanation for one of the most enduring mysteries of human experience, which is the question of why resonances in musical instruments and the rhythmic beating of drums can often evoke the deepest emotional response in the human soul. I propose that the musical instrument represents man's first modest success at replicating the physical principle behind biological computation, and that the strong emotional response evoked by these inanimate resonances reflects an unconscious recognition of the essential affinity between mind and music.
If music is a manifestation of resonances in the brain, then the observed structures and patterns of music can offer clues to the operational principles of the brain. The study of musical scales relates directly to the theory of higher harmonics, and the lawful patterns of melody observed across cultures offer a glimpse into the way the brain encodes temporal information, in symmetrical and periodic patterns that tend to cycle endlessly. It would be very instructive to construct resonating systems whose natural modes of oscillation were tuned to generate endless streams of melody in endlessly original patterns, but following the basic rules of harmony and structure that people find aesthetically pleasing. I suspect that a mechanism capable of generating random melodies would also serve as a pattern recognition system, encoding the pattern of observed events in terms of the periodic melody that best matches those aperiodic events. There is ample opportunity for interesting research in this direction, which would unite the specialties of neuroscience, resonance, and music theory.
If the natural resonance of the brain generates endless streams of patterned melody, then the corresponding resonance in the visual domain is seen in the patterns of visual ornament throughout history and across all human cultures, such as those shown below. Although there is a great deal of variation in the ornament of different cultures, there is also much that is common between them. In particular, factors such as balance, harmony, symmetry, and periodicity, as well as an elegant simplicity of the component forms, are universal laws of aesthetics, and therefore likely to be organically founded.

Mary Waller (1961) observed the similarity between standing wave patterns in the Chladni figures and common themes in ornamental design, a key link between aesthetics and harmonic resonance. Helmholtz (1863, 1964) discovered a similar link between aesthetics and harmonic resonance, in his theory of consonance of musical tones. These findings suggest that patterns which are aesthetically pleasing, match well to the eigenfunctions of perceptual representation, and can thus be used to map out those eigenfunctions.
If visual ornament is a result of resonances in the visual brain, then the patterns of ornament can be used to direct the search for a resonating mechanism with the properties of the visual cortex, by devising resonating systems specifically to generate endless streams of ornamental patterns in endlessly original configurations, but following the basic rules of harmony and structure that people find aesthetically pleasing. I propose that the resulting mechanism would also serve as a useful pattern recognition system, encoding the spatial pattern of the stimulus image in terms of the ornamental patterns that best match it. There is ample opportunity for interesting research in this direction.
It occasionally happens in science that changing one initial assumption can fundamentally alter our view of the science as a whole. Such is the case in neuroscience with the phenomenon of visual experience. Once we acknowledge that the vivid spatial structures in our experience are patterns in our own brain, that immediately raises the spatial problem in visual representation: How does the brain construct its exquisitely detailed three-dimensional moving colored images? It is only in the context of this larger question that harmonic resonance appears as a plausible explanation. Standing waves offer a principle of spatial representation that is far more flexible and adaptive than the spatial receptive fields of the neural network paradigm, and they offer a holistic global principle of perceptual computation consistent with Gestalt theory.
But once the possibility of harmonic resonance is given serious consideration, evidence in support of harmonic resonance appears from a great variety of diverse sources. Harmonic resonance is consistent with the oscillatory nature of neural spiking, and with the notion of synchronous oscillations in the cortex across objects perceived as a perceptual whole, or visual gestalt. Harmonic resonance is consistent with the evidence from electro-encephalograms (EEG) that show coherent global oscillations across the brain as a whole, with a characteristic cyclic pattern of oscillation that correlates with different functional brain states. Harmonic resonance also accounts for a number of aesthetic phenomena, from musical rhythm, melody, and harmony, to patterns of ornament and aesthetic design, to patterns of symmetry and periodicity in dance, to symmetry and periodicity in animal locomotion, like the cyclic motion of the legs of a centipede, and the sinusoidal undulations of fish and snakes. All of these diverse phenomena point to a single explanation, that the animal brain employs spatial standing waves in both static, and endlessly repeating cyclic patterns, to express the spatial patterns of body posture in both sensory and motor function, and to express the spatial patterns of visual experience. If it turns out to be right, the potential significance of this theory to neuroscience can hardly be overstated.
Grossberg S, Mingolla E, 1985 "Neural Dynamics of Form Perception:
Boundary Completion, Illusory Figures, and Neon Color Spreading"
Psychological Review 92 173-211.
Grossberg S, Todorovic D, 1988 "Neural Dynamics of 1-D and 2-D
Brightness Perception: A Unified Model of Classical and Recent
Phenomena" Perception and Psychophysics 43, 241-277.
Helmholtz H. L. F. (1954) On the sensations of tones as a
physiological basis for the theory of music. New York:
Dover. (Original work published in 1863)
Lehar S. (1994) "Directed Diffusion and Orientational Harmonics:
Neural Network Models of Long-Range Boundary Completion through
Short-Range Interactions". Ph.D. Thesis, Boston University. Available
at
Lehar S. (1999a) "Computational Implications of Gestalt Theory 1: A
Multi-Level Reciprocal Feedback (MLRF) to Model Emergence and
Reification in Visual Processing". Rejected Cognitive Psychology
November 2000. Available at
Lehar S. (1999b) "Computational Implications of Gestalt Theory 2: A
directed diffusion to model collinear illusory contour
formation". Rejected Cognitive Psychology November 2000. Available at
Lehar S. (2003a) "The World In Your Head: A Gestalt view of the
mechanism of conscious experience." Mahwah NJ: Erlbaum. Additional
information available at
Lehar S. (2003b) "Gestalt Isomorphism and the Primacy of the
Subjective Conscious Experience: A Gestalt Bubble Model". The
Behavioral and Brain Sciences 26(4), 375-444. Also available at
Lehar S. (2003c) "Directional Harmonic Theory: A Computational Gestalt
Model to Account for Illusory Contour and Vertex
Formation". Perception 32(4) 423-448. Also available at
Waller, M. D. (1961) Chladni Figures: A study in symmetry. London:
G. Bell & Sons.
http://cns-alumni.bu.edu/~slehar/webstuff/thesis/thesis.html
http://cns-alumni.bu.edu/~slehar/webstuff/orivar/orivar1.html
http://cns-alumni.bu.edu/~slehar/webstuff/orivar/orivar2.html
http://cns-alumni.bu.edu/~slehar/webstuff/book/WIYH.html
http://cns-alumni.bu.edu/~slehar/webstuff/bubw3/bubw3.html
http://cns-alumni.bu.edu/~slehar/webstuff/dirhr1/dirhr1.html