
There are a few common themes that run throughout my work from my PhD thesis to my latest books. One is the validity of modeling perceptual experience directly, as it is experienced, which in vision is in the form of explicit spatial images. Another is the dynamic emergent nature of perceptual processes, and an attempt to model them using the kind of analogical spatial logic suggested by Gestalt theory, like the logic of the soap bubble, or of the flexible wooden spline, as they relax into their lowest energy configurations. A key goal has been to express the vague and general Gestalt concepts of emergence and reification in concrete computational terms, as a necessary prerequisite for identifying the corresponding neurophysiological mechanism.
In my Ph.D. thesis ( Lehar1994) I extended the work of Grossberg & Mingolla (1985), and Grossberg & Todorovicz (1988) on the computational modeling of visual illusions, such as the Kanizsa figure. My focus was on modeling the illusory contour in cases where the inducing stimulus edges are not in strict collinear alignment, as in the figures below.

Psychophysical studies show a greater tolerance for a bending mis-alignment, as in (a) and (b) above, than for a shearing mis-alignment as in (c) and (d). Grossberg & Mingolla account for these phenomena by way of elongated cooperative receptive fields, cells that are so positioned as to receive input from two spatially displaced inducing edges, and thus mark the illusory contour between them. However that model cannot account for the asymmetry in the data above. Furthermore, large receptive fields inevitably suffer from spatial averaging effects, which tend to produce broad fuzzy patches of activation instead of a sharp linear contour as observed. (Lehar 1994, 1999b)
I proposed a more dynamic analog Gestalt approach to illusory contour formation by way of a spatial diffusion of activation outward from all stimulus edges, as suggested below left. When two such extrapolated edges come into spatial alignment, they link up to produce an emergent illusory contour, as suggested below right. The final contour is not defined by any single receptive field, but by a stream of directed energy diffusing through many smaller fields of influence whose collective action determine the dynamics of the final percept. Computer simulations of the directed diffusion model show that with a simple architecture it exhibits the asymmetry between bending and shearing mis-alignments, with a sharp clear contour, that are difficult to explain with a neural receptive field model.

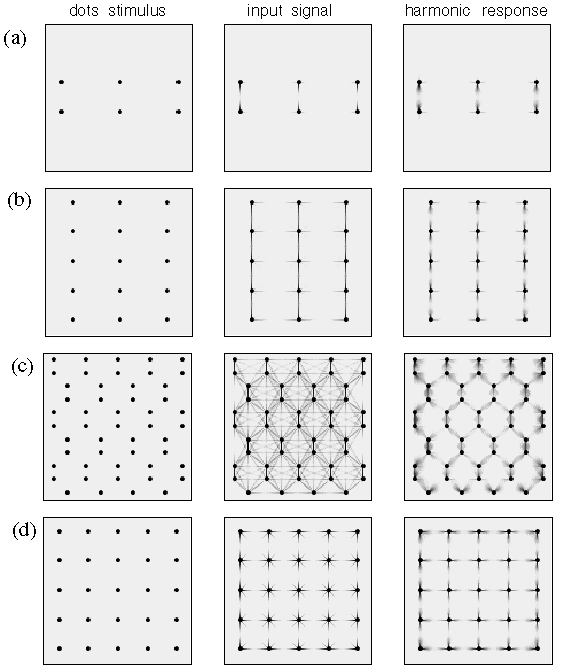
A second focus of my PhD thesis was on the issue of illusory vertex formation, where one, two, three, or more illusory contours meet at a sharp vertex, as seen in the illusory dot groupings shown below. The perceived groupings at each dot are shown in magnified form on the right. This kind of illusory grouping phenomenon is extremely challenging for a neural network or receptive field model, because it would require spatial templates for each of the vertex types observed below, each replicated at every location, and at every orientation at every location. This is just one manifestation of the combinatorial explosion in the number of receptive fields required for the simplest spatial recognition and completion by way of a neural network model, which does not bode well for the neural network paradigm as a concept for spatial representation in the brain.

I found that all of the illusory effects can be explained by a directional harmonic resonance, or spatial standing waves of different harmonics of directional periodicity. (Lehar 1994, 2003c) The figure below shows the first four harmonics of directional periodicity, representing vertices composed of one, two, three, or four illusory contours that meet at a vertex.
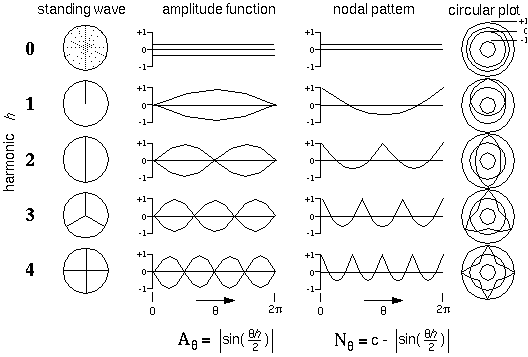
The next figure below shows computer simulations of the dot patterns above, showing how each of these grouping phenomena correspond to one or another harmonic of directional periodicity. Unlike the neural network approach, there is no need for spatial templates at every location and orientation across the visual field, there is now just a resonance that emerges spontaneously in response to certain patterns in the stimulus. This is a very significant finding, because it finally offers an escape from the combinatorial limitations of the spatial receptive field, and thus it provides a promising approach to addressing the spatial problem in neural representation.
I was fascinated by the principle of reification in perception, the constructive, or generative function behind the formation of illusory contours and illusory surfaces in Gestalt illusions. I could see a general principle in a number of illusory phenomena, from the Craik-O'Brien-Cornsweet effect, to the brightness contrast illusion, to the Kanizsa figure. In all of these phenomena it seemed as if higher order features, such as the illusory contours, that are presumably detected at a higher level of the visual hierarchy, appear to be projected top-down to appear as actual surfaces of a particular brightness in our experience. I proposed a general principle of perceptual representation by reification, that is, the top-down feedback from higher to lower levels in the visual hierarchy performs the inverse of the corresponding bottom-up transformation, and the purpose of this inverse transformation is to couple the representations throughout the visual hierarchy with reciprocal bottom-up top-down connections in order to establish a globally-consistent state. (Lehar 1999a)
For example the figure below left represents one manifestation of the conventional feed-forward concept of the visual hierarchy, beginning with a surface brightness image, corresponding to the input stimulus. The next level performs an edge detection to produce a polar boundary image, somewhat like the response of cortical simple cells, and the level above that discards the contrast polarity information to produce the apolar boundary image, somewhat like complex cell response. Finally a higher cooperative level performs the collinear boundary completion to produce the illusory contours, somewhat like hypercomplex cells. But at this high level of the representation there is neither contrast across edges, nor complete surface percepts, those must be constructed by top-down reification as shown below right. The cooperative image is transformed top-down into the apolar boundary image, now including the illusory contours constructed at the higher level, and that image is further transformed to a polar boundary image, complete with illusory contours with a direction-of-contrast added, and that image in turn is reified to a full surface brightness percept, complete with a spatial filling-in of the illusory surface. Here is a system that does not just perform bottom-up recognition, as in the feature detection or "grandmother cell" concept, but it also performs top-down reification or filling-in of an explicit and detailed image at the lowest level, constructed on the basis of all of the higher levels above it. The system can in principle operate entirely endogenously, or in top-down mode, as in dreams and hallucinations. This is a truly novel and significant concept of perceptual processing.
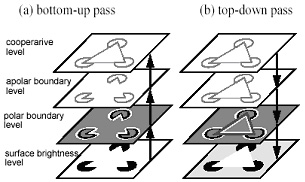
The significance of this reification function of top-down processing is that it finally resolves the notion of a hierarchical visual representation, which is suggestive of a feed-forward processing stream, with the parallel emergent nature of experience identified by Gestalt theory, and it accounts for the constructive or generative function of perception, as well as providing an explanation for the feedback pathways observed in the brain.
Computer simulations of this bottom-up top-down hierarchy reproduced the Craik-O'Brien-Cornsweet illusion, the brightness contrast illusion, and the Kanizsa figure, showing how all of these diverse phenomena reflect a single bottom-up/top-down principle of bottom-up abstraction to locate higher order alignments and regularities, and top-down reification to "paint" the implications of those discovered regularities back at the surface brightness level. (Lehar 1999a, 1999b)
The same principle of bottom-up abstraction and top-down completion occurs just as well in three-dimensional spatial perception. When we see the stimulus shown below, we interpret patches of the two-dimensional stimulus as the exposed faces of objects and surfaces in the world, and the configuration of those exposed surfaces in turn stimulates a perceptual experience of whole objects complete through their hidden rear faces. We "know" their hidden spatial limits almost as well as their exposed frontal limits just by the shape of their front faces, and this perceptual completion occurs by a kind of completion by symmetry, extrapolating and interpolating the regularity detected in the exposed faces into the hidden rear portions of the perceived volumes.
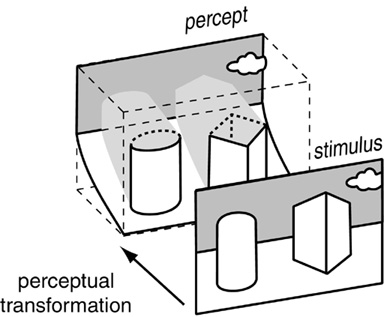
This process of perceptual reification is clearly evident in the volumetric illusory percepts below, where every point on every illusory surface exhibits a distinct depth value, and a surface orientation in depth, that together define continuous spatial surfaces that bound volumetric regions of experience. Whatever the neurophysiological mechanism might be behind this experience, the information content of that mechanism is that of a volumetric spatial experience.

As a consequence of numerous debates with colleagues, and exchanges with various reviewers, I gradually became aware of a profound paradigmatic gulf between na´ve realists who believe that the world of experience is the real world itself, and representationalists who understand that the world of experience is itself merely a representation, which is distinct from the objective external world that it replicates in effigy. To my surprise I discovered that a significant majority of contemporary philosophers, psychologists, and neuroscientists, subscribe either implicitly or explicitly to the na´ve realist view of perception. Resolving this paradigmatic gulf became the prime focus of my first book (Lehar 2003a), and of a paper recently published by the Behavioral & Brain Sciences (BBS) journal. (Lehar 2003b) In those works I show that na´ve realism is untenable, and that the many common objections to the representationalist thesis are unfounded.
The idea of perception as a literal volumetric replica of the world inside your head immediately raises the question of boundedness-that is, how an explicit spatial representation can encode the infinity of external space in a finite volumetric system. The solution to this problem can be found by inspection. Phenomenological examination reveals that perceved space is not infinite but is bounded. This can be seen most clearly in the night sky, where the distant stars produce a domelike percept that presents the stars at equal distance from the observer, and that distance is perceived to be less than infinite.
Consider the phenomenon of perspective, as seen for example when standing on a long straight road that stretches to the horizon in a straight line in opposite directions. The sides of the road appear to converge to a point up ahead and back behind, but while converging, they are also perceived to pass to either side of the percipient, and at the same time the road is perceived to be straight and paralell throughout its entire length. This prominent violation of Euclidean geometry offers clear evidence for the non-Euclidean nature of perceived space. For the two sides of the road must in some sense be perceived as being bowed, and yet while bowed,they are also perceived as being straight. Objects in the distance are perceived to be smaller, and yet at the same time they are also perceived to be undiminished in size. This can only mean that the space within which we perceive the road to be embedded must itself be curved. (Lehar 2003a, 2003b)
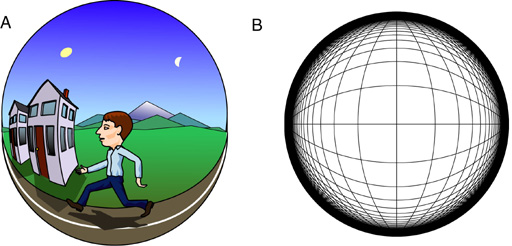
What does it mean for a space to be curved? If it is the space itself that is curved, rather than just the objects within that space, then it is the definition of straightness itself that is curved in that space, as suggested by the curved grid lines in B above. In other words, objects that are curved to conform to the curvature of the space, are by definition straight in that curved space. If you are having trouble picturing this paradoxical concept and suspect that it embodies a contradiction in terms, just look at phenomenal perspective, which has exactly that paradoxical property. Phenomenal perspective embodies that same contradiction in terms, with parallel lines meeting at two points in opposite directions, while passing to either side of the percipient, and while being at the same time straight and parallel and equidistant throughout their length. This absurd contradiction is clearly not a property of the physical world, which is measurably Euclidean, at least at the familiar scale of our everyday environment.
In fact the observed warping of perceived space is exactly the property that allows the finite representational space to encode an infinite external space. This property is achieved by using a variable representational scale: the ratio of the physical distance in the perceptual representation relative to the distance in external space that it represents. This scale is observed to vary as a function of distance from the center of our perceived world, such that objects close to the body are encoded at a larger representational scale than objects in the distance, and beyond a certain limiting distance the representational scale falls to zero, that is, objects beyond a certain distance lose all perceptual depth, like the stars on the dome of the night sky. This Gestalt Bubble concept of spatial representation provides a unique way of presenting an infinite volumetric space in a finite volumetric representation, with spatial distortions exactly as observed in phenomenal perspective.
The Gestalt Bubble concept of spatial representation emphasizes another aspect of perception that is often ignored in models of vision: that our percept of the world includes a percept of our own body in that world, and our body is located at a very special location at the center of that world, and it remains fixed at the center of perceived space even as we move about in the external world. Perception is embodied by its very nature, for the percept of our body is the only thing that gives an objective measure of scale in the world. (Lehar 2003a, 2003b)

One of the most disturbing properties of the phenomenal world for models of the perceptual mechanism involves the subjective impression that the phenomenal world rotates relative to our perceived head as our head turns relative to the world, and that objects in perception are observed to translate and rotate while maintaining their perceived structural integrity and recognized identity. This suggests that the internal representation of external objects and surfaces is not anchored to the tissue of the brain, as suggested by current concepts of neural representation, but that perceptual structures are free to rotate and translate coherently relative to the neural substrate. This issue of brain anchoring is so troublesome that it is often cited as a counter-argument against representationalism, since it is difficult to conceive of the solid spatial percept of the surrounding world having to be reconstructed anew in all its rich spatial detail with every turn of the head. However an argument can be made for the adaptive value of a neural representation of the external world that could break free of the tissue of the sensory or cortical surface in order to lock on to the more meaningful coordinates of the external world, if only a plausible mechanism could be conceived to achieve this useful property.
But whatever the neurophysiological mechanism underlying perception, we can determine the basic functionality, or information processing function apparent in perception by inspection. Whichever direction I direct my gaze, in that direction I see in greater detail and resolution a portion of the volumetric spatial world that I sense to surround me in all directions. It is as if the two-dimensional retinal image from the spherical surface of the retina is copied onto a spherical surface in front of the eyeball of the perceptual effigy, from whence the image is projected radially outward in an expanding cone into the depth dimesion, as suggested below, as an inverse analog of the cone of light received from the world by the eye. Eye, head, and body orientation relative to the external world are taken into account in order to direct the visual projection of the retinal image into the appropriate sector of perceived space, as determined from proprioceptive and kinesthetic sensations in order to update the image of the body configuration relative to external space.
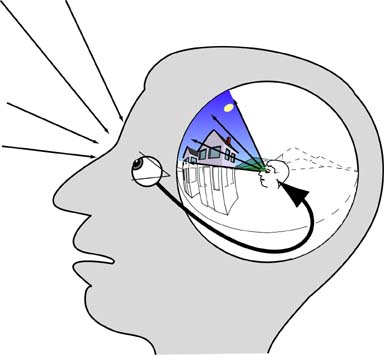
Successive glances in different directions gradually build up a volumetric picture of surrounding space, as a vivid modal experience within the visual field, with the highest resolution at the center of foveal vision, and an amodal experience of space and volume in the hidden rear portion outside the visual field. I can reach back and locate the rear surface of my own head, and various walls and floors behind me, by extrapolation of those volumes and surfaces from their visible portions within the visual field.

From my Ph.D. thesis to my latest books, the breadth and scope of my work has confirmed the wisdom of the perceptual modeling approach, to model the experience of spatial vision as it is experienced, independent of considerations of neurophysiological plausibility. The perceptual modeling approach highlights the constructive, or generative function of perception, or how perceptual processes construct a complete volumetric spatial world, complete with a copy of our own body at the center of that world. None of these aspects of experience are even hinted at by the best modern neurophysiological findings. In fact, there is a dimensional mismatch between the concept of individual neurons connected by discrete synapses, and the spatially continuous volumetric world of our experience. The representational strategy used by the brain is an analogical one; that is, objects and surfaces are represented in the brain not by an abstract symbolic code, or in the activation of individual cells or groups of cells representing particular features detected in the visual field. Instead, objects are represented in the brain by constructing full spatial effigies of them that appear to us for all the world like the objects themselves-or at least so it seems to us only because we have never seen those objects in their raw form, but only through our perceptual representations of them.
The harmonic resonance theory of spatial representation finally offers a plausible solution to the profound spatial problem in the brain, that circumvents the combinatorial problems inherent in a neural network or spatial template solution to this problem. The spatial standing wave is far more flexible and adaptive than the corresponding neural receptive field, because the standing wave is not anchored to the tissue of the brain, and thus it can rotate and translate and flex elastically within the tissue of the brain, without the need for explicit spatial templates for every one of the possible shapes that it can take. Standing waves can also define cyclic patterns of motion in motor control, as evident in the wavelike undulations of fish and snakes, and the periodic/cyclic motion of a centipedes' feet. Harmonic resonance, by its nature, promotes both symmetry and periodicity in simple and compound hierarchical forms, and that preference for symmetry and periodicity is clearly manifest throughout human aesthetic design. It is seen in the symmetry and periodicity of ornamental design, from Gothic cathedrals to the Alhambra, from patterns on wallpaper and fabric, to pots and vases. All of these are manifestations of higher resonances in the brain.