A Gestalt Bubble Model

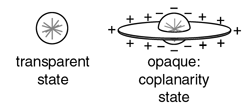
I propose a volumetric matrix of local computational elements, each of which can be in one of two states, transparent or opaque, to represent the perception of transparency or of a colored surface as every location in visual space. The perceptual transformation can now be expressed as the "turning on" of opaque state units in the proper configuration in response to a visual stimulus.

Surface Percept Interpolation

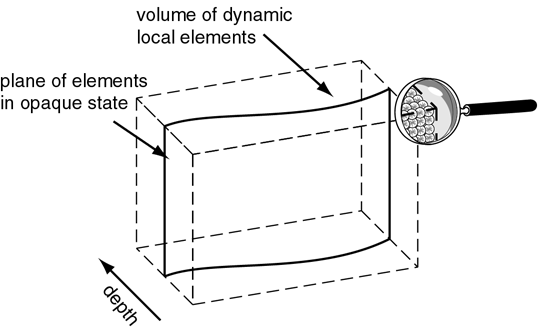
In order to account for spatial interpolation in perception, the opaque state units also take on a surface orientation value that represents the perceived orientation of a perceived surface through that point in visual space. Opaque state elements interact with one another by way of local fields of influence, whose effect is to induce transparent-state elements within their field of influence to switch to the opaque state, and opaque-state elements to rotate to an orientation that is closer to parallel to the orientation of the field.

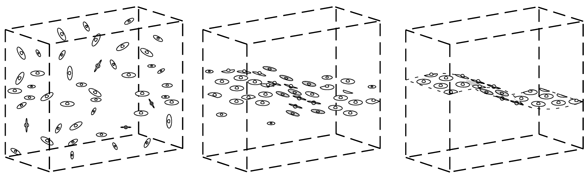
The influence is reciprocal between neighboring elements, as required by emergence, so that if the system is initialized with elements randomly assigned to the transparent or the opaque state, with opaque-state elements being assigned random surface orientation values, any initial inhomogeneity in the distribution will tend to feed back on itself, resulting in the formation of an emergent surface percept, like a soap bubble surface in the volumetric matrix. This surface is free to bend and stretch like a real soap bubble, except that this bubble is not a real physical surface, but merely a pattern of activation in a volumetric representation. This model now accounts for the spatial interpolation function in perception by way of an emergent principle of computation.