Chapter 1: The Two Worlds of Reality

Steven Lehar

slehar@cns.bu.edu

The brain is wider than the sky,

For, put them side by side,

The one the other will contain

With ease, and you beside.

---

Emily Dickenson

The Philosophical Divide in Theories of Vision

The scientific investigation into the nature of biological vision has been plagued over the centuries by a persistent confusion over a central philosophical issue. Simply stated, this issue involves the question whether the world we see around us is the real world itself, or whether it is merely a copy of the world presented to consciousness by our brain in response to input from our senses. In philosophical terms, this is the distinction between direct realism, as opposed to indirect realism. Although it is not much discussed in contemporary neuroscience, this issue is of the utmost significance to our understanding of the nature of visual processing, Indeed the issue is most often either avoided altogether, or when it is mentioned, it is usually passed off as a pseudoproblem. However the issue is very real and very significant, and the frequent evasive handling of it can be traced to the fact that current theories of neurocomputation are often based implicitly on the direct realist view that the world we see around us is the world itself. This view however is demonstrably wrong on logical grounds, and therefore most theories of visual processing and representation can be shown to be founded on false assumptions.

The direct realist view, also known as naive realism, is the natural intuitive understanding of vision that we accept without question from the earliest days of childhood. When we see an object, such as this book that you hold in your hands, the vivid spatial experience of the book is assumed to be the book itself. This assumption is supported by the fact that the book is not merely an image, but appears as a solid three- dimensional object that emits sounds when we flip its pages, emits an odor of pulp and ink, and produces a vivid spatial sensation of shape, volume, texture, and weight as we manipulate it in our hands. Our belief in the reality of our perceived world is continually reaffirmed by the stability and permanence of objects we perceive in the world. Nevertheless, there are deep logical problems with the direct realist view that cannot be ignored if we are ever to understand the true nature of perceptual processing.

The problem arises if we accept the modern materialistic view of the brain as the organ of consciousness. According to this view, every aspect of visual experience is a consequence of electrochemical interactions within our physical brain in response to stimulation from the eyes. In other words, there is a direct correspondence between the physical state of the brain, and the corresponding subjective experience, such that a change of a particular sort in the physical brain state results in a change in the subjective experience, and conversely, any change in the subjective experience reflects some kind of change in the underlying brain state. It follows therefore that a percept can be viewed in two different contexts, either from the objective external context, as a pattern of electrochemical activity in the physical brain expressed in terms of neurophysiological variables such as electrical voltages or neural spiking frequencies, and from the internal subjective context where that same percept is viewed as a subjective experience expressed in terms of subjective variables such as perceived color, shape, or motion, etc. Like the two faces of a coin, these very different entities can be identified as merely different manifestations of the same underlying structure. The dual nature of a percept is analogous to the representation of data in a digital computer, where a pattern of voltages present in a particular memory register can represent some meaningful information, either a numerical value, or a brightness value in an image, or a character of text, etc. when viewed from inside the appropriate software environment, while when viewed in external physical terms that same data takes the form of voltages or currents in particular parts of the machine.

However this materialistic view of perception, which is generally accepted in modern neuroscience, is at odds with a most fundamental property of visual experience, i.e. the fact that objects of the visual world are experienced as outside of ourselves, in the world itself, rather than within our brain where we assume the neurophysiological state to be located within our head. (See Harrison 1989 and Smythies 1994 for an insightful discussion of the problem and its implications.) The flow of visual information is exclusively unidirectional, from the world through the eye to the brain. The causal chain of vision clearly shows that the brain cannot experience the world out beyond the sensory surface, but can register only the data transmitted to it from the sensory organs. In other words if your subjective experience of the vivid spatial percept of this book corresponds to physical processes occurring within your brain, then in a very real sense this book too, as you perceive it, is also necessarily located within your physical brain. A percept cannot escape the confines of our physical brain into the world around us any more than the pattern of voltages in a digital computer can escape the confines of particular wires and registers within the physical mechanism.

Neither can the external nature of perception be explained by the fact that internal patterns of energy in our physical brain are connected to external objects and surfaces by reference, any more than the voltages encoded in a computer register can be considered to be external to a computer just because they refer to the external values which they represent. Although a sensor may record an external quantity in an internal register or variable in a computer, from the internal perspective of the software running on that computer, only the internal value of that variable can be "seen", or can possibly influence the operation of that software. In exactly analogous manner the pattern of electrochemical activity that corresponds to our conscious experience can take a form that reflects the properties of external objects, but our consciousness is necessarily confined to the experience of those internal effigies of external objects, rather than of external objects themselves. And yet we observe in subjective experience the perceptual structures and surfaces of our world of experience as present external to our bodies, as if superimposed on the external world in a manner that appears to have no correspondence to the manner of representation in a digital computer.

It is the external nature of perception which has led many philosophers through the ages to conclude that there is something deeply mysterious about consciousness, which is forever beyond our capacity to fully comprehend. As Searle (1992) explains, when we attempt to observe consciousness, we see nothing but whatever it is we are conscious of; that there is no distinction between the observation and the thing observed. It seems impossible in principle to endow a robotic intelligence with the powers of external perception the way we experience our own visual world. For a robot cannot in principle experience the world directly, but only through the image projected by the world on the sensory surface of the robot's electronic eye. Unless we invoke mystical processes beyond the bounds of science, this same limitation must also hold for human and animal perception, i.e. we can only know that which occurs within our brain, which is the organ of conscious experience. How then can we explain the external nature of the visual world as observed in subjective experience?

Kant's Insight into the Dual Nature of Reality

The solution to this paradox was discovered centuries ago by Immanuel Kant (1781) with the concept of indirect realism. Kant argued that there are in fact two worlds of reality, which he called the nouminal and the phenomenal worlds. The nouminal world is the objective external world, which is the source of the light that stimulates the retina. This is the world studied by science, and is populated by invisible entities such as atoms, electrons, and invisible forms of radiation. The phenomenal world is the internal perceptual world of conscious experience, which is a copy of the external world of objective reality constructed in our brain on the basis of the image received from the retina. The only way we can perceive the nouminal world is by its effects on the phenomenal world. Therefore the world we experience as external to our bodies is not actually the world itself, but only an internal virtual reality replica of that world generated by perceptual processes within our head.

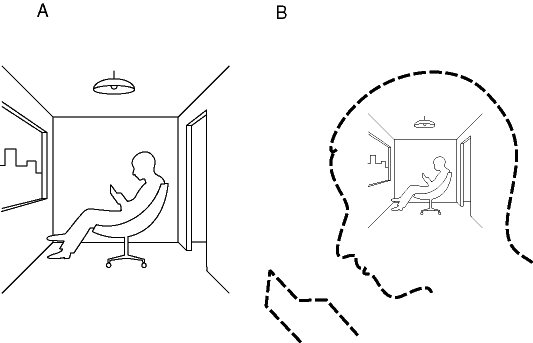
The distinction between these two views of perception is illustrated schematically in figure 1. In the direct realist view, your perceptual experience of the world around you as you sit reading this book is identified as the world itself, i.e. you perceive yourself where you sit, surrounded by your physical environment, as suggested in figure 1 A. In the indirect realist view of perception, the world you see around you is identified as a miniature perceptual copy of the world contained within your real physical head, as suggested schematically in figure 1 B. The nouminal world and your nouminal head are depicted in dashed lines, to indicate that these entities are invisible to your direct experience.

Figure 1

A: Your perceptual experience of the world as you sit reading this book, as conceptualized in the direct realist view of perception. B: The true situation as conceived in the philosophy of indirect realism, where your percept of the world around you is identified as an internal pattern in your head, the real external world (shown in dashed lines) being beyond your direct experience.

According to this view, consciousness is indeed directly observable, contrary to Searle's contention, for the objects we experience as being in the world around us are the products, or "output" of consciousness rather than the "input" to it, and the experience of a three-dimensional object occupying some portion of perceived space is also a direct observation of consciousness, and only in secondary fashion is that percept also representative of an objective external entity. This remarkable insight into the true nature of reality ranks with those other great revolutions in our view of our place in the cosmos, such as the fact that the earth is round rather than flat as it appears locally, or that the earth rotates under the sun rather than the reverse as it appears from the earth's surface, or that solid objects contain more empty space than solid matter, as they appear perceptually. However although Kant's great insight is now over two centuries old, this basic fact of human experience is not generally taught in school, and even more remarkably, neither is it generally known or even discussed in those sciences where it would be of the utmost relevance. Instead, theories of perception and neural representation continue to be advanced which are based either explicitly or implicitly on direct realist assumptions.

The reason for the persistent confusion over this issue is that Kant's insight is particularly difficult to visualize or to explain in unambiguous terms. For example even the description of the causal chain of vision is itself somewhat ambiguous, since it can be interpreted in two alternative ways. Consider the statement that light from this page stimulates an image in your eye which in turn promotes the formation of a percept of the page up in your brain. The ambiguity inherent in this statement can be revealed by the question "where is the percept?". There are two alternative correct answers to this question, although each is correct in a different spatial context. One answer is that the percept is up in your head, (the one you point to when asked to point to your head) which is correct in the external or direct realist context of your perceived head being identified with your objective physical head, and since your visual cortex is contained within your head, that must also be the location of the patterns of energy corresponding to your percept of the page. The problem with this answer however is that no percept is experienced within your head where you imagine your visual cortex to be located. The other correct answer is that the percept of the page is right here in front of you where you experience the image of a page. This answer is correct in the internal spatial context of the entire perceived world around you being within your head. However the problem with this answer is that there is now no evidence of the objective external page that serves as the source of the light. The problem is that the vivid spatial structure you see before you is serving two mutually inconsistent roles, both as a mental icon representing the objective external page which is the original source of the light, and as an icon of the final percept of the page inside your head; i.e. the page you see before you represents both ends of the causal chain. And our mental image of the problem switches effortlessly between the internal and external contexts to focus on each end of the causal chain in turn. It is this automatic switching of mental context that makes this issue so elusive, because it hinders a consideration of the problem as a whole.

The Differential Analyzer

In the 1950's Vannevar Bush at MIT developed a mechanical analog computer which, although rapidly made obsolete by the emergence of the new digital electronic computer, nevertheless demonstrated some intriguing computational principles which are unique to that paradigm, and suggestive of the nature of biological computation. The differential analyzer, as the machine was called (see Fifer 1961 for a thorough review of analog computation) consisted of an array of parallel shafts that rotated on finely machined bearings, mounted on a table. Each shaft represented a variable, whose value was encoded by the total angle that the shaft had rotated from some reference angle or origin. The shafts were interconnected by orthogonal cross-shafts through a variety of ingenious mechanical devices that performed various mathematical operations, such as addition, multiplication, integration, etc. So for example if one shaft represented a variable x, and another represented t, a third shaft y could be defined to represent y = integral(x)_dt by connecting it by cross-shafts to the other two shafts through a mechanical integrator mechanism. The integrator expressed the integral function in literal analog fashion, so that the rotation of shaft y was always literally equal to integral(x)_dt however shafts x and t happened to be turned. So the variable y took on its meaning not just by definition, but by its functional connection to the rest of the machine. More complex differential equations were built up in this manner from simpler elements to arbitrary levels of complexity, to solve dynamic equations that were prohibitively computational- intensive by other means. Any physical system that can be described in mathematical terms can thus be simulated in physical analogy by the differential analyzer.

The differential analyzer was not easy to program, for it required a different mechanical configuration of shafts and gears for every equation that it was set to solve, so the device was rapidly superceded first by the more flexible analog electronic computer, and then by the even more programmable digital computer. But the differential analyzer exhibits some unique characteristics that demonstrate the power of the analogical paradigm. Although the device was generally used as an input / output device, with certain variables being fixed as input in order to compute an output value on other free variables, this kind of mechanism can in principle be operated just as well in reverse, turning the output shafts and observing the resultant rotation of the input shafts, thereby performing the inverse function of the original one. More generally, once a particular functional relationship between variables has been established in the mechanism, any combination of these variables can be fixed, to observe the the effects on the values, or degrees of freedom, of the remaining unconstrained variables.

This same principle of computation can be further elaborated. Instead of defining some variables as rigidly fixed and others as free, variables can be given an intermediate status by means of mechanical spring forces that tend to push or drive them in a particular direction. For example if a variable is connected to a particular system so as to represent a measure of economy, or profit, or any other measure of desirable attribute of the modeled system, a spring force can then be applied to that shaft to express the desire to maximize that economy or profit or whatever, and that desire force will be communicated to all of the other free variables in the system as communicated through the intermediate functional transformation mechanisms. In fact any number of spring forces can be applied to any of the variables in the system to express even more complex combinations of constraints, and the dynamic state of the system will evolve under the collective action of all of those physical constraints communicated in parallel through the system. This kind of system can therefore even address problems which are mathematically underconstrained, by installing gentle spring forces that pull the system state towards any desired quadrant of the solution space. This concept of computation does not have the input / output structure characteristic of so many of our mathematical and computational formalisms, for the influences between the variables propagate through the system in all directions simultaneously.

I propose that the higher levels of symbolic representation in biological computation, as expressed in human reasoning, exhibit this parallel analog computational strategy between symbolic variables. The lower levels of perceptual processing also have this analog dynamic nature, but they have an additional spatial nature, as suggested in the plotting room analogy, where spatial concepts are expressed in literal spatial form. This allows the constraints, or desired solutions states of the system to be expressed as attractive or repulsive spatial forces in a spatial replica of external space, as a spatial computation in a spatial medium.

Internal v.s. External Representation

The analog spatial strategy presented above is reminiscent of the kind of computation suggested by Braitenberg (1984) in his book Vehicles. Braitenberg describes very simple vehicles that exhibit a kind of animal-like behavior by way of very simple analog control systems. For example Braitenberg describes a light-seeking vehicle equipped with two photocells connected to two electric motors that power two driving wheels. In the presence of light, the current from the photocells drives the vehicle forward, but if the light distribution is non-uniform and one photocell receives more light than the other, the vehicle will turn either towards or away from the light, depending on how the photocells are wired to the wheels. One configuration produces a vehicle that exhibits light-seeking behavior, like a moth around a candle flame, whereas with the wires reversed the same vehicle will exhibit light-avoiding behavior, like a cockroach scurrying for cover when the lights come on. The behavior of these simple vehicles is governed by the spatial field defined by the intensity profile of the ambient light, and therefore, like the analogical paradigm, this type of vehicle also performs a spatial computation in a spatial medium. However in the case of Braitenberg's vehicles, the spatial medium is the external world itself, rather than an internal replica of it. Rodney Brooks (1991) elevates this concept to a general principle of robotics, whose objective is "intelligence without representation". Brooks argues that there is no need for a robotic vehicle to possess an internal replica of the external world, because the world can serve as a representation of itself. O'Regan (1992) extends this argument to human perception, and insists that the brain does not maintain an internal model of the external world, because the world itself can be accessed as if it were an internal memory, except that it happens to be external to the organism. Nevertheless information from the world can be extracted directly from the world whenever needed, just like a data access of an internal memory store.

However there is a fundamental flaw with this concept of perceptual processing, at least as a description of human perception. For unless we invoke mystical processes beyond the bounds of science, then surely our conscious experience of the world must be limited to that which is explicitly represented in the physical brain. In the case of Braitenberg's vehicles, that consciousness would correspond to the experience of only two values, i.e. the brightness detected by the two photocells, and the conscious decision-making processes of the vehicle (if it can be called such) would be restricted to responding to those two values with two corresponding motor signals. These four values therefore represent the maximum possible content of the vehicle's conscious experience. The vehicle has no idea of its location or orientation in space, and its complex spatial behavior is more a property of the world around it than of anything going on in its "brain". Similarly, if the world is indeed accesses as an external memory, as suggested by O'Regan, our conscious experience cannot extend to portions of that external memory which are not currently being "accessed", or copied into an internal representation in the brain. We should never see in visual consciousness the world around us as a structural whole, but only as a sequence of local fragments that change with each saccade. But this description is inconsistent with our subjective experience. For when we stand in a space, like a room, we experience the volume of the room around us as a simultaneously present whole, every volumetric point of which exists as a separate parallel entity in our conscious experience, even in monocular viewing. Braitenberg's vehicles can be programmed to go to the center of a room by placing a light at that location, but the vehicle cannot conceive of the void of the room around it or the concept of its center, for those are spatial concepts that require a spatial understanding. We on the other hand can see the walls, floor, and ceiling of a room around us simultaneously, embedded in a perceived space, and we can conceptualize any point in the space of that room in three dimensions without having to actually move there ourselves. The world of visual experience therefore clearly demonstrates that we possess an internal map of external space like the Fighter Command plotting room, and the world we see around us is exactly that internal representation.

Symbol Grounding by Spatial Analogy

The analogical spatial paradigm offers a solution to some of the most enduring and troublesome problems of perception. For although the construction and maintenance of a spatial model of external reality is a formidable computational challenge (see chapters 4 through 6, and chapter 10), the rewards that it offers makes the effort very much worth the trouble. The greatest difficulty with a more abstracted or symbolic approach to perception has always been the question of how to make use of that abstracted knowledge. This issue was known as the symbol grounding problem (Harnad 1990) in the propositional paradigm of representation promoted by the Artificial Intelligence (AI) movement. The problem of vision, as conceptualized in AI, involves a transformation of the two-dimensional visual input into a propositional or symbolic representation. For example an image of a street scene would be decomposed into a list of items recognized in that scene, such as "street", "car", "person", etc., as well as the relations between those items. Each of these symbolic tags or labels is linked to the region of the input image to which it pertains. The two-dimensional image is thereby carved up into a mosaic of distinct regions, by a process of segmentation (Ballard & Brown 1982, p. 6-12), each region being linked to the symbolic label by which it is identified. Setting aside the practical issues of how such a system can be made to work as intended, (which itself turns out to be a formidable problem) this manner of representing world information is difficult to translate into practical interaction with the world. For the algorithm does not "see" the street in the input image as we do, but rather it sees only a two-dimensional mosaic of irregular patches connected to symbolic labels. Consider the problem faced by a robotic vehicle designed to find a mail box on the street and post a letter in it. Even if an image region is identified as a mail box, it is hard to imagine how that information could be used by the robot to navigate down the street and avoid obstacles along the way. What is prominently absent from this system is a three-dimensional consciousness of the street as a spatial structure, the very information that is so essential for practical navigation through the world. A similar problem is seen in the feature detection paradigm that suggests a similar decomposition of the input image into an abstracted symbolic representation.

An analogical representation of the street on the other hand would involve a three-dimensional spatial model, like a painted cardboard replica of the street complete with a model of the robot's own body at the center of the scene. It is the existence of such a three-dimensional replica of the world in an internal model that, I propose, constitutes the act of "seeing" the street. Setting aside the issue of how such a model can be constructed from the two-dimensional image, (which is also a formidable problem) making practical use of such a representation is much easier than for a symbolic or abstracted representation. For once the mailbox effigy in the model is recognized as such, it can be marked with an attractive force, and that force in turn draws the effigy of the robot's body towards the effigy of the mailbox in the spatial model. Obstacles along the way are marked with negative fields of influence, and the spatial algorithm to get to the mailbox is to follow the fields of force, like a charged particle responding to a pattern of electric fields.

The analogical paradigm can also be employed to compute the more detailed control signals to the robot's wheels. The forward force on the model of the robot's body applies a torque force to the model wheels, but the model wheels cannot respond to that force directly. Instead, that torque in the model is interpreted as a motor command to the wheels of the larger robot to turn, and as larger wheels begin to turn in response to that command, that turning is duplicated in the turning of the model wheels, as if responding directly to the original force in the model world. Side forces to steer the robot around obstacles can also be computed in similar fashion. A side force on the model robot should be interpreted as a steering torque, like the torque on the pivot of a caster wheel. That pivoting torque in the model is interpreted as a steering command to pivot the larger wheels, and the steering of the larger wheels is then reflected in the steering of the model wheels also. The forces impelling the model robot through the model world are thereby transformed into motor commands to navigate the real robot through the real world. However obstacles in the real world that might block the larger wheels from turning or pivoting as commanded, would prevent their smaller replicas from turning also, thereby communicating the constraints of the external world back in to the internal model. Unlike Braitenberg's vehicles, this robot has a spatial "consciousness" or awareness of the structure of the world around it, for it can feel the simultaneous influence of every visible surface in the scene, which jointly influence its motor behavior. For example the robot navigating between obstacles in its path feels the repulsive influence of all of them simultaneously, and is thereby induced to take the path of least resistance weaving between them like a skier on a slalom course, on the way to the attractive target point. Our own conscious experience clearly has this spatial property for we are constantly aware of the distance to every visible object or surface in our visual world, and we can voluntarily control our position in relation to those surfaces, although what we are actually "seeing" is an internal replica of the world rather than the world itself. This is not the whole story of consciousness, for there remains a deeper philosophical issue with regard to the ultimate nature of conscious experience, or what Chalmers (1995) refers to as the "hard problem" of consciousness. However the analogical paradigm addresses the functional aspect, or the "easy problem" of consciousness by clarifying the functional role of conscious experience, and how it serves to influence behavior.

The idea of motor planning as a spatial computation has been proposed in field theories of motor control, as discussed in chapter 10, in which the intention to walk towards a particular objective in space is expressed as a field-like force of attraction, or valence, between a model of the body, and a model of the target, expressed in a spatial model of the local environment. The target is marked with a positive valence, while obstacles along the way are marked with negative valence. When we see an attractive stimulus, for example a tempting delicacy in a shop window at a time when we happen to be hungry, our subjective impression of being physically drawn towards that stimulus is not only metaphorically true, but I propose that this subjective impression is a veridical manifestation of the mental mechanism that drives our motor response. For the complex combination of joint motions responsible for deviating our path towards the shop window are computed in spatial fashion in a spatial model of the world, exactly as we experience it to occur in subjective consciousness. Indeed the spatial configuration of the positive and negative valence fields evoked by a particular spatial environment can be inferred from observation of its effects on behavior, in the same way that the pattern of an electric field can be mapped out by its effects on moving charged particles. For example the negative valence field due to an obstacle such as a sawhorse placed on a busy sidewalk can be mapped by observing its effect on the paths of people walking by. Although the influence of this obstacle is observed in external space, the spatial field that produces that behavioral response actually occurs in the spatial models in the brains of each of the passers-by individually.

Another example of a spatial computational strategy can be formulated for the problem of targeting a multi-jointed limb, i.e. specifying the multiple angles required of the individual joints of the limb in order to direct its end-effector to a target point in three-dimensional space. This is a complex trigonometrical problem that is underconstrained. However a simple solution to this complex problem can be found by building a scale model of the multi-jointed limb in a scale model of the environment in which the limb is to operate. The joint angles required to direct the limb towards a target point can be computed by simply pulling the end-effector of the model arm in the direction of the target point in the modeled environment, and recording how the model arm reacts to this pull. Sensors installed at each individual joint in the model arm can be used to measure the individual joint angles, and those angles in turn can be used as command signals to the corresponding joints of the actual arm to be moved. The complex trigonometrical problem of the multi-jointed limb is therefore solved by analogy, as a spatial computation in a spatial medium.

There is evidence to suggest that this kind of strategy is employed in biological motion. For when a person reaches for an object in space, their body tends to bend in a graceful arc, whose total deflection is evenly distributed amongst the various joints to define a smooth curving posture, i.e. the motor strategy serves to minimize a configural constraint expressed in three-dimensional space, thus implicating a spatial computational strategy. The dynamic properties of motor control are also most simply expressed in an external spatial context. For the motion of a person's hand while moving towards the target describes a smooth arc in space and time, accelerating uniformly through the first half of the path, and decelerating to a graceful stop through the second half. In other words the observed behavior is exactly as if the person's body were indeed responding lawfully to a spatial force of attraction between the hand and the target object in three-dimensional space, which in turn suggests that a spatial computational strategy is being used to achieve that result. Further evidence comes from the subjective experience of motor planning, for we are unaware of the individual joint motions when planning such a move, but rather our experience is more like a force of attraction that seems to pull our hand towards the target object, and the joints in our arm seem to simply follow our hand as it responds to that pull. This computational strategy generalizes to any configuration of limbs with any number of joints, as well as to continuous limbs like a snake's body or an elephant's trunk. This same strategy also applies globally to the motion of the body as a whole through the environment.

The analogical concept of perceptual computation couples the functions of sensory and motor processing by way of an interface expressed neither in sensory nor in motor terms, but in a modality-independent structural code representing objects and surfaces of the external world. Perceptual processes construct the volumetric spatial model based on information provided by the sensory input. Attentional and motivational processes mark objects or regions of that model with positive and negative valence, and those regions in turn project spatial valence fields that pervade the volumetric void of the perceived world like the electric fields projected by charged objects. Motor processes then compute the response of a structural model of the body to the valence fields expressed in the structural model of the surrounding environment.

Structural Properties of the Spatial Model

If the world of conscious experience, in both its structural and functional aspects, is a veridical manifestation of processes taking place in the physical brain, as it must of necessity be, this in turn validates a phenomenological approach to the investigation of biological computation. The phenomenological approach offers a unique perspective into the workings of the mind, which in turn sets constraints for the corresponding workings of the brain. Phenomenological examination reveals that the perceptual model of the external world is more than a mere replica of the visible surfaces in the world, but rather it is a meaningful decomposition of those surfaces into coherent objects, and those objects are perceived to extend beyond their visible surfaces. For we experience objects perceptually not as the hollow facade defined by their visible front surfaces, but as complete volumetric wholes which we perceive to extend in depth, and whose outer surfaces are perceived to enclose the perceived object even around its hidden rear face. For example your view of the front face of this book in your hands generates a percept of the book as a solid spatial object, whose hidden rear faces are filled-in or reified from the information of the visible front face, as well as from the sensation of the rear face sampled at discrete points by your fingers, with the help of your general knowledge of the shape of books. Thought and knowledge are generally discussed as if they were non-spatial abstractions. The phenomenological approach reveals that thought can also take the form of volumetric structures that appear in a volumetric model of space. This is plainly evident for "perceptual thoughts", as seen in the volumes and surfaces of the phenomenal world. However phenomenology also reveals the existence of more abstract mental constructs which are nevertheless experienced as volumetric spatial forms. Although the hidden portions of an object are experienced in an invisible or ghostly amodal manner, the percept of those hidden portions is nevertheless a volumetric spatial structure, for it is possible to reach back behind an object like a sphere or cylinder, or the back of this book, and indicate with your palm the approximate location and surface orientation at any sample point on the hidden surface, based only on the view of the visible front face of that object. This exercise, which I call morphomimesis, provides evidence for the rich spatial structure in perceptual experience. Although your hand can mime only one such invisible surface at a time, the entire hidden structure of a perceived object is experienced simultaneously as a structural volume embedded in perceived space, as indicated by the shape your hand takes as you prepare to grasp the book by its hidden rear face. Similarly, when an object is partially occluded by a foreground object, like the portion of the world hidden behind this book, we perceive it to exist nevertheless as a perceptual whole, with the missing portions filled in perceptually where we know them to exist. Again, the information encoded in that perceptual experience is expressed in an invisible amodal form, but the spatial structure of that experience can again be revealed by morphomimesis.

A similar form of perceptual reification is seen in the percept of the world hidden behind your head. That world is also experienced as a vivid spatial void occupied by the spatial structures of the floor on which you stand, or the chair on which you sit, as well as the walls that enclose the room behind your back, extrapolated from the visible portions of those surfaces that fall within the visual field. That is why we can reach back to scratch our ear, or pick up a coffee cup or pencil from a surface behind us without necessarily having to look back to guide our hand to its target. Much of this information is usually acquired from earlier views of those now-hidden surfaces. But whether it is learned or immediately perceived, that information is nevertheless encoded in explicit spatial form, like a structural model of the room around you that extends into space behind you, if only in a fuzzy probabilistic, but essentially spatial manner.

Functional Properties of the Spatial Model

In order for the perceptual model of the world to be a meaningful representation of it, the model must be more than just a structural replica of the configuration of objects and surfaces, but the model must also replicate the essential laws and forces of the world to lend meaning to observed motions in the world. For we perceive objects to posses not only color, shape and size, but we also experience them to posses mass and weight and impenetrability, as well as permanence, in the sense that we do not expect them to spontaneously appear or disappear without cause. Again, these aspects of knowledge are usually considered to be non-spatial abstractions. However the properties such as mass and impenetrability are perceived to pervade a specific volume of perceived space corresponding exactly to the volume of the perceived object to which they apply. These higher order properties that we perceive objects to posses in various combinations have a direct influence on our understanding of their behavior when observed in perception, as well as on our predictions of the possible behavior of those objects under hypothetical circumstances. For example if a moving object which is perceived to have a certain shape and color disappears momentarily behind an occluder, it is expected to reappear at the other side with the same shape and color, and at the precise moment determined by its perceived velocity and the length of the occluded path. In other words the object is tracked perceptually even while concealed behind the occluder, as a volumetric image of a particular shape, color, location, and velocity, although the percept is experienced in amodal form through the occlusion. If a moving object is observed racing towards a solid wall, its perceived momentum and impenetrability results in an expectation that it will impact the wall with an audible report, after which it will be expected to either be flattened or shattered by the impact, or to bounce back elastically after contact with the wall, depending on the properties of the material of which it is perceived to be composed. If no such change is observed after the collision, this will result in a fundamental change in the perceived properties of that object. For example if the object passes effortlessly through the wall, the object will suddenly be perceived to be insubstantial, like a ghost, or the beam of a searchlight, i.e. it will lose its perceived impenetrability. If on the other hand the object stops dead on contact with the wall, it will immediately lose its perceived mass, like a block of styrofoam striking a sticky surface. If it smashes powerfully through the wall, it will be perceived to be massive. These modifications of the perceived properties of the object seem to propagate "backwards in time", as if the perceived object had been penetrable, or massless all along. Similarly, objects perceived to have weight are expected perceptually to accelerate towards the ground whenever they are perceived to be unsupported, while objects that are observed to hover with no visible means of support are perceived to be weightless like a balloon. The perceived higher order properties of objects can therefore be considered as a perceptual shorthand that predicts the motions of those objects under a wide variety different circumstances, while those properties themselves are inferred from the observed behavior of their object.

The perceptual model of the external world therefore is a direct physical analog of the world, akin to a physical model constructed of components that posses actual mass and weight and impenetrability, although in the brain those objects must be composed of nothing more than patterns of electrochemical activation that somehow mimic those external forces and properties. Since the objects of which the perceived world is constructed exert simulated forces on each other, some configurations of perceived objects will be more stable than others. For example the percept of a solid block of granite floating over the ground with no visible means of support exerts a powerful downward force of simulated gravity in the perceptual representation. But if the sensory stimulus that produces the percept is static, then the synthetic gravity in the perceptual model must be balanced either by an imagined upward force of invisible support, or the granite must lose its perceived weight. Either of these perceptual interpretations are unlikely in the real world, and therefore that percept will be unstable, as if seeking out a more reasonable explanation. The percept of a granite block resting on the ground on the other hand is a more stable configuration, because the simulated forces of gravity and support are symmetrically balanced, and therefore no unseen or improbable forces are needed to stabilize the percept. According to this view of perception therefore, a meaningful understanding of the world corresponds to the construction of a functional copy of the world in an internal representation, complete with functional relations and laws of motion that replicate the laws and forces of the physical world. The physical laws embodied in the perceptual mechanism do not correspond exactly to the laws of physics as discovered by science, encoding instead what is known as naive physics, i.e. physical principles as they are understood intuitively by the non-scientist.

Abstract Thought and Cognition

The higher order functions of cognition and mental imagery can also be studied by introspective observation. Mental images often take the form of solid three-dimensional objects that can move about in space, and those images can be manipulated under voluntary control in order to test various spatial hypotheses, for example when picturing a new arrangement of furniture, or planning a construction project. The nature of the mental image is itself amodal, like the ghostly percept of the hidden rear faces of objects. But the spatial reality and volumetric nature of the mental image can also be demonstrated by morphomimesis, for example by polishing the imaginary faces of an imagined sphere or cube with your hands, using sweeping motions that conform to the invisible surfaces of the imagined form wherever you choose to locate it in perceived space. The ability to manipulate such imaginary spatial constructs offers clear evidence for the spatial nature of at least some cognitive abstractions. In chapter 9 I propose that amodal perception, as of occluded objects in the world, is a primitive or lower form of mental imagery, and that mental imagery and cognition evolved from that lower level function of amodal perception. The idea of mental imagery as the essential principle behind cognition enjoyed more popularity in the early days of psychology, before modern notions of neurocomputation rendered them neurophysiologically implausible. Besides the troublesome issue of how thoughts can take the form of three-dimensional spatial structures, there was always the deeper problem of how abstract ideas could possibly be encoded as a mental image. In chapter 9 I propose a solution to this issue, again based on phenomenological observation. For although the mental image of an abstract concept such as "furniture" is experienced as a fuzzy non-spatial form, that abstraction can also be reified under voluntary control, to appear as a particular piece of furniture, such as a chair, and that chair can be further reified to appear in the mental image at any desired orientation, location, and scale, as well as in any color or furniture style. It is the very flexibility and indeterminate nature of the abstract mental image that give it its power of abstraction, for the abstraction, even in its most indeterminate, form can be processed in mental manipulations, for example when imagining an unspecified piece of furniture standing in a corner of a real room, or imagining a "thing" resting in your hand. The fuzzy indeterminate nature of the mental abstraction therefore is not to be taken as evidence for its non-spatial nature, but only as evidence for its fuzzy indeterminate nature. For the mental abstraction appears as a kind of probabilistic superposition of multiple possible shapes, but spatial shapes nonetheless, that can under voluntary control be reified in any or all of their dimensions of variability, or they can be manipulated in indeterminate form as fuzzy probabilistic entities.

Neurophysiological Considerations

At some level the properties of subjective experience as outlined above, such as the vivid spatial nature of the world of perception and the analogical influences they exert on our behavior, are so plainly manifest in everyday experience as to hardly require psychophysical confirmation. However theories of perceptual processing very rarely take account of these most obvious properties of experience. The reason for this is that these properties are inconsistent with contemporary understanding of neurophysiology. Ever since Santiago y Cajal confirmed the cellular basis of the nervous system, a concept known as the Neuron Doctrine has come to dominate psychology. For the input / output function of the neural dendrites and axon, together with the relatively slow transmission across the chemical synapse suggests that neurons operate as quasi-independent processors in a sequential or hierarchical architecture that processes information in well defined processing streams. This idea was captured by Sherrington's evocative image of the brain as "an enchanted loom where millions of flashing shuttles weave a dissolving pattern, always a meaningful pattern though never an abiding one." (Sherrington 1937, p. 173) However the neuron doctrine is inconsistent with the properties of the subjective experience of vision. Our experience of a visual scene is not at all like an assembly of abstract features, or millions of flashing shuttles, but rather our percept of the world is characterized by a stable and abiding experience of solid volumes, bounded by colored surfaces, embedded in a spatial void. There is a dimensional mismatch between this world of volumes and surfaces, and the constellation of discrete activations suggested by the neuron doctrine. Far from being a reduced or abstracted featural decomposition of the world, the world of perceptual experience encodes more explicit spatial information than the sensory stimulus on which it is based. There is no accounting in the neuron doctrine for this constructive or generative aspect of perceptual processing. Sherrington himself acknowledged this disparity between physiology and phenomenology. (Sherrington 1937, p. 228-9)

Contemporary neuroscience therefore finds itself in a state of serious crisis, for the more we learn about the details of neurophysiology, the farther we seem to get from an explanation of the most fundamental properties of the world of visual experience. The great disparity between our knowledge of neurophysiology and the properties of subjective visual experience has led neuroscientists in recent decades to ignore the subjective conscious experience of vision, and to adopt by default a naive realist view that excludes the phenomenal world from the set of data to be explained by neuroscience. This approach of shrinking the scope of the problem of vision to fit the simplistic models proposed to explain it, has been responsible for the emergence of a long series of sterile neurocomputational models that bear no resemblance to the most significant and interesting aspects of vision clearly apparent in the world of visual experience. In fact the "bottom-up" approach that works upwards from the properties of neurons measured neurophysiologically, and the "top-down" approach that works downwards from the subjective experience of perception are equally valid and complementary approaches to the investigation of the visual mechanism. Both approaches are essential because each approach offers a view of the problem from its own unique perspective. Eventually these opposite approaches to the problem must meet somewhere in the middle. However to date, the gap between them remains as large as it ever was. I propose that the problem is a paradigmatic one, i.e. one that cannot be resolved by simply specifying the right neural network architecture, but that the atomistic concept of computation embodied in the neuron doctrine must itself be replaced by a more holistic paradigm.

If the most central concept behind modern neuroscience is indeed in error, how then are we to model the computational operations of perception in the absence of a plausible neurophysiological theory to define the elements of which our model is to be composed? In this book I present a perceptual modeling approach, as discussed in chapter 2, i.e I propose to model the percept as it is experienced subjectively, rather than the neurophysiological mechanism by which that experience is supposedly subserved. This is only an interim solution however, for ultimately the neurophysiological basis of neurocomputation must also be identified. However the perceptual modeling approach can help to quantify the information processing apparent in perception, as a necessary prerequisite for a search for a neurophysiological mechanism that can perform the equivalent computational transformation. This approach leads to a very different view of perceptual processing than that suggested by the neural network approach inspired by neurophysiology. In chapters 4 through 6 I present a model of the computational transformations manifest in perceptual processing expressed in terms that are independent of any particular theory of neural representation, that reveals the unique computational principles that are operative in perception.

Harmonic Resonance Theory

The properties of perceptual processing revealed by the perceptual modeling approach are deeply perplexing, not only in terms of the underlying neurophysiological mechanism, but even in more general terms of theories of computation and representation. For the holistic global aspect of perception identified by Gestalt theory represents the polar opposite to the atomistic sequential processing strategy embodied both in the neuron doctrine, as well as in the paradigm of digital computation. The preattentive nature of Gestalt phenomena, and their universality across individuals independent of past visual experience suggest that these enigmatic Gestalt phenomena reflect a fundamental aspect of perceptual computation. I contend that no significant progress can possibly be made in our understanding of perceptual processing until the computational principles behind Gestalt theory have been identified.

In fact there is one physical phenomenon that exhibits exactly those same enigmatic Gestalt properties, and that is the phenomenon of harmonic resonance, or the emergence of spatial structure in patterns of standing waves in a resonating system. In chapter 8 I present a Harmonic Resonance Theory of neurocomputation as an alternative to the neuron doctrine paradigm. For like the spatial receptive field of the neuron doctrine, the standing wave defines a spatial pattern in the neural substrate. Unlike the receptive field model, the spatial pattern defined by harmonic resonance is not a rigid template-like entity hard-wired in a cell's receptive field, but a more elastic, adaptive mechanism, like a rubber template, that automatically deforms to match any deformation of the input pattern.

Harmonic resonance also exhibits invariances in a unique form. In a circular-symmetric resonating system like a circular flute, or a spherical resonating cavity, the pattern of standing waves within that cavity maintains its structural integrity as it rotates within it. This offers an explanation for the rotation invariance observed in perception that has been so difficult to account for in conventional neurocomputational terms.

Another unique property of harmonic resonance is that resonances in different modules or sub-systems tend to couple with each other to define a single global resonance that synchronizes the individual resonances in the sub-systems in such a way that a modulation of the resonance in one sub-system will be communicated immediately and in parallel to all the other sub-systems of the coupled system. This unique property of harmonic resonance offers a solution to the question of the "binding problem", and the unity of the conscious experience, as will be discussed in chapters 6 and 8. This concept therefore offers an explanation for the global resonances observed across the entire cortex in Electroencephalogram (EEG) recordings. Furthermore, harmonic resonance offers a functional explanation for the phenomenon of synchronous spiking activity observed across widely separated cortical areas, a phenomenon that is somewhat problematic for the neuron doctrine, because the phase of spiking activity should not be preserved across the chemical synapse. According to the Harmonic Resonance model, this synchronous activity is not a signal in its own right between individual neurons, but is an epiphenomenon of a global standing wave pattern that spans those remote cortical areas.

The Harmonic Resonance theory also offers an explanation for the fuzzy indeterminate nature of the mental images of abstract concepts. For like the mental image, the standing wave pattern can take on a fuzzy indeterminate form, somewhat like a superposition of multiple states or of a continuous range of states, each of which individually defines an explicit reified spatial structure. The harmonic resonance model therefore offers a computational solution to many of the most troublesome issues of perceptual computation. I propose therefore that harmonic resonance is the computational principle behind the enigmatic holistic properties of perception identified by Gestalt theory.

A Psycho-Aesthetic Hypothesis

The harmonic resonance theory of neurocomputation also accounts for a number of other aspects of human experience which have never found a satisfactory explanation elsewhere. For the most prominent characteristics of harmonic resonance are symmetry and periodicity of the standing wave patterns both in space and in time. It turns out that symmetry and periodicity have very special significance in human experience, for these properties are ubiquitous in human aesthetics, as seen in the symmetrical and periodic patterns of design used in all cultures throughout human history to decorate clothing, pots, tools and other artifacts, especially items of special symbolic or religious significance. Symmetry and periodicity are also prominent features of architecture, music, poetry, rhythm, and dance. In chapter 11 I propose a psycho-aesthetic hypothesis, whereby any principles of aesthetics that are found to be universal across all human cultures, are thereby indicative of properties that are fundamental to the human mind itself, rather than a cultural heritage. I propose therefore that the symmetry and periodicity in art and music are aesthetically pleasing exactly because they are easily encoded in the periodic basis function offered by the harmonic resonance representation.

Besides providing collateral support for the harmonic resonance theory, the psycho-aesthetic hypothesis can be inverted to identify even more properties of mental function than those revealed by phenomenological analysis alone. For the primitives of the visual arts, music, and dance, can be seen as evidence for the nature of visual, auditory, and motor primitives in the brain. This in turn suggests a periodic basis set in perception, in the nature of a Fourier code. The advantage of a periodic basis set is that when a match is found to an input pattern, the periodic basis set automatically extrapolates that pattern outward in space and time, reifying the unseen portions of the pattern on the basis of the sample present in the input. This perceptual extrapolation explains the amodal completion of hidden portions of perceived objects and surfaces in the world. Evidence for this periodic basis set can be seen even in the abstract world of mathematics, where the periodicity inherent in the number line reflects an attempt to quantify the world in terms of periodic patterns. This insight serves to unite the fields of science and aesthetics, and reveals mathematics as a more abstracted refinement of the same principles observed in the visual and musical arts, which in turn are merely a more abstracted refinement of the principles behind visual and auditory perception, as discussed in chapter 11. The harmonic resonance theory also offers an explanation for one of the most enduring mysteries of human experience, which is the question of why resonances in musical instruments and the rhythmic beating of drums have such a powerful ability to evoke the deepest emotional response in the human soul. I propose that the musical instrument represents man's first modest success at replicating the physical principle behind biological computation, and the strong emotional response evoked by these inanimate resonances reflects an unconscious recognition of the essential affinity between mind and music.