
Submitted to Cognitive Psychology July 2000
Rejected November 2000
Neurophysiological investigations of the visual system by way of single-cell recordings have revealed a hierarchical architecture in which lower level areas, such as the primary visual cortex, contain cells that respond to simple features, while higher level areas contain cells that respond to higher order features apparently composed of combinations of lower level features. This architecture seems to suggest a feed-forward processing strategy in which visual information progresses from lower to higher visual areas. However there is other evidence, both neurophysiological and phenomenal, that suggests a more parallel processing strategy in biological vision, in which top-down feedback plays a significant role. In fact Gestalt theory suggests that visual perception involves a process of emergence, i.e. a dynamic relaxation of multiple constraints throughout the system simultaneously, so that the final percept represents a stable state, or energy minimum of the dynamic system as a whole. A Multi-Level Reciprocal Feedback (MLRF) model is proposed to resolve the apparently contradictory concepts, by proposing a hierarchical visual architecture whose different levels are connected by bi-directional feed-forward and feedback pathways, where the computational transformation performed by the feedback pathway between levels in the hiararchy is a kind of inverse of the transformation performed by the corresponding feed-forward processing stream. This alternative paradigm of perceptual computation accounts in general terms for a number of visual illusory effects, and offers a computational specification for the generative, or constructive aspect of perceptual processing revealed by Gestalt theory.
Neurophysiological investigations of the visual system by way of single-cell recordings have revealed a hierarchical architecture in which lower level areas, such as the primary visual cortex, contain cells that respond to simple features, while higher level areas contain cells that respond to higher order features apparently composed of combinations of lower level features. This architecture seems to suggest a feed-forward processing strategy in which visual information progresses from lower to higher visual areas. This concept of processing is consistent with artificial vision algorithms that also process visual information in a series of stages, each stage extracting higher order visual information from the output of the previous lower-level stage. However there is other evidence that suggests a more parallel strategy in biological vision, in which top-down feedback plays a significant role. Neurophysiological and histological studies have identified reciprocal pathways from higher to lower level areas, which are as extensive as the bottom-up pathways that they mirror. Gestalt theory also provides phenomenological evidence suggestive of some kind of top-down feedback, for a number of visual illusions demonstrate that global configural factors play an important role in perception. For example Figure 1 a shows the camouflage triangle (camo-triangle) whose sides are defined by a large number of apparently chance alignments of visual edges. As soon as the global triangular form is recognized in this figure, the low level visual edges of which it is composed stand out from the other randomly oriented edges, and appear at high resolution, linking up the apparently random edge fragments by way of invisible or amodal contours. Other illusions generate visible or modal illusory edges and surfaces which are virtually indistinguishable from actual edges and surfaces in a stimulus, as seen in the Kanizsa figure shown in Figure 1 b. This suggests that the global configural information, presumably detected in higher level areas, is propagated back down to the lower levels where it appears to enhance or amplify specifically those lower-level features that are consistent with the global gestalt.

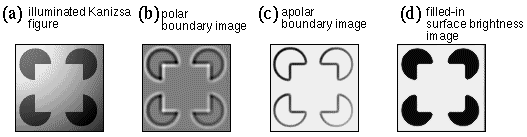
Figure 1.(a)The camoflage illusory triangle (camo triangle) demonstrates the principle of emergence in perception, because the figure is perceived despite the fact that no part of it can be detected locally. (b) The Kanizsa illusory triangle. (c) The subjective surface brightness percept due to the Kanizsa stimulus. (d) The amodal contour percept due to the Kanizsa stimulus, where the darkness of the gray lines represents the salience of a perceived contour in the stimulus.
However it is not quite clear how this top-down influence might be expected to occur. For one of the most appealing features of the hierarchical concept of visual processing is that it appears to involve a principle of abstraction from lower to higher levels in the representation, i.e. the information encoded in the lower levels is reduced to a more abbreviated, or compressed representation at the higher levels. Even at the level of the retina, the rods and cones respond to absolute light intensity, whereas the retinal ganglion cells respond only to brightness transitions across visual edges, in the manner of an edge image, with no response within regions of uniform brightness. In the primary visual cortex, a simple cell is generally sensitive to the contrast polarity of the oriented edge to which it responds, responding perhaps to a dark/light edge of a particular orientation but not to a light/dark edge of that same orientation, whereas the higher level complex cells generally respond to edges of either contrast polarity of a particular orientation. This suggests that the complex cell is connected to pairs of lower-level simple cells of opposite contrast polarity, either of which is capable of stimulating the contrast-invariant higher-level cell. In other words the simple cell responses across the primary visual cortex encode information as in a contrast-edge image, whereas the complex cell responses represent a contrast-insentive edge image, like a pen-and-ink line drawing.
Invariance to a variety of factors seems to be a general property of biological vision. For example visual recognition often exhibits invarience to the rotation, translation, and spatial scale of the stimulus object. This kind of invariance involves a many-to-one relation between the multiple possible configurations of the stimulus and the single invariant response that it promotes presumably at the higher levels of the visual hierarchy. It is not clear therefore how that high-level representation can be meaningfully communicated back down the visual hierarchy in top-down feedback, for that would require a one-to-many transformation from the invariant form to its many possible configurations of lower-level features. For example a top-down feedback from a complex cell to the pair of simple cells that trigger it would stimulate opposite contrast polarities simultaneously, which would have to cancel each other at the simple cell level since they represent mutually contradictory lower level interpretations of the higher level feature. A similar problem arises in the more general case of rotation, translation, and scale invariance. For if many possible variations of the stimulus can all trigger the same high level recognition node, top-down feedback from that higher-level node would stimulate every possible rotation, translation, and scale of the recognized form. Those multiple activations would blur together to produce an amorphous field of general activation at the lower levels of the visual hierarchy, like a superposition of every possible variation of the stimulus object, rather than a single image of the recognized object at a particular rotation, translation, and scale.
Gestalt theory offers a general principle of computation to account for feedback in perceptual processing. For Gestalt theory suggests that visual processing occurs by a process of emergence, a dynamic relaxation of multiple constraints throughout the system simultaneously (Köhler 1920), so that the final percept represents a stable state, or energy minimum of the system as a whole. The principle of emergence is seen in the camo triangle, where the local influence of the individual edge fragments link up to define the global form, and that form in turn feeds back to enhance specifically those edge fragments that are consistent with the global gestalt. Koffka (1935) exemplified the concept of emergence with the analogy of the soap bubble, whose global shape emerges under the simultaneous action of innumerable local forces. The final spherical shape is therefore determined not by a rigid template of that shape, but by a lowest-energy configuration of the system as a whole, and that whole is in a state of dynamic balance, such that a disturbance of any part of the system will lead to a general reconfiguration of the system as a whole. A key characteristic of this kind of emergent process is the principle of reciprocal action (köhler 1920) between the elements of the system. For example if a portion of the bubble pushes on a neighboring portion in a certain direction, that neighbor will either succumb to the force with little resistance, or if it is constrained by opposing forces, for example by the wire hoop on which the bubble is anchored, that resistance is communicated back reciprocally to the original element, pushing on it in the opposite direction. The information in this kind of emergent system therefore does not progress from input to output in a feed-forward manner, but propagates forwards, backwards, and in every other direction throughout the system simultaneously, like the forces of surface tension that unite the various parts of the bubble surface.
The different levels of a hierarchical representation express visual information in different codes, or featural representations. The feed-forward processing therefore involves a series of transformations between the codes at those different levels. If emergence is to be implemented in a hierarchical visual representation therefore, this would have to mean that the top-down transformations from higher to lower levels should be in some sense the inverse of their corresponding bottom-up transformations, in order to preserve the different representationals codes in the various levels of the hierarchy. In cases where the bottom-up transformation performs an abstraction from the lower to the higher level, for example from a surface brightness to an edge based representation, then the corresponding top-down transformation must perform a reification, the inverse of abstraction, filling in the perceptual information that was lost bottom-up, in this case transforming an edge based representation back to a surface brightness based representation. Exactly how this reification might occur in general is the principal focus of the present paper. In general terms I propose that the top-down processing does indeed attempt to reify every possible variation of the low level featural configuration simultaneously in a one-to-many manner, each of those many lower-level variations being consistent with the higher level representation recognized in the scene. However that reification is not determined exclusively by top-down feedback, but it is also constrained or channelled by the configuration of the input stimulus. In other words the bottom-up and top-down processing streams interact at every level of the hierarchy, as suggested by the principle of emergence. The product or "output" of this kind of system is therefore not to be found at either the highest or lowest levels of the hierarchy, as suggested by the feed-forward sequential paradigm of computation, but at all levels of the hierarchy simultaneously, each level encoding the interpretation of the input stimulus in the representational code specific to that level, for example surface brightnesses at lower levels, and edges or abstracted features at higher levels.
I propose therefore a Multi-Level Reciprocal Feedback (MLRF) model of visual processing in order to resolve the concept of parallel emergence and feedback suggested by Gestalt theory, with the hierarchical architecture suggested by neurophysiology. I do not however propose a specific neurophysiological model, nor a specific model of visual processing. The focus here is only on the general principle of a bi-directional coupling through a visual hierarchy composed of multiple levels that each express visual information in different representational codes, with lower levels encoding a more explicit and expansive representation of the stimulus, while higher levels encode progressively more abstracted or reduced representations of the same stimulus. In order to clarify and demonstrate this general concept, I present an example system using components commonly employed in neural network models of vision, although in this system those components are adapted to perform simultaneous bottom-up and top-down processing. The example system demonstrates abstraction, or information compression at every stage of bottom-up processing, and an inverse reification, or filling-in function in the complementary top-down processing, that effectively inverts the corresponding transformation in the bottom-up processing stream. I will show that this principle of information processing accounts in general terms for a variety of visual illusory phenomena. This paradigm therefore offers a quantitative characterization of the computational principles behind the constructive or generative aspect of visual processing revealed by Gestalt theory.
One of the greatest difficilties in proposing computational models of biological vision is that little is known with any certainty about the actual computational and representational principles employed in the brain. It has become fashionable in recent decades to express models of visual processing in neural network terms, even models formulated to account for psychophysical rather than neurophysiological data. While the desire to bridge the gap between physiology and phenomenology is understandable, there is a problem with modeling perceptual phenomena in neurophysiological terms, for until a mapping has been established between neurophysiology and the corresponding subjective experience, there is no way to know whether the proposed model has correctly replicated the psychophysical phenomena that is is designed to explain. In effect, neural network models attempt to solve two problems at the same time, i.e. to propose a computational model of a particular perceptual phenomenon, and at the same time to propose a specific representational scheme to map physiology to phenomenology. One of the problems with this approach is that there is a fundamental mismatch between the dimensions of conscious experience and current theories of neural representation. For the world of visual experience is composed of continuous colored surfaces separated by bounding edges, whereas contemporary concepts of neural representation suggest a more abstracted, or featural representation in which the activation of particular cells in the brain supposedly corresponds to the detection of particular features present in the visual field. There is no clear consensus as to how the experience of a continuous field of color should be expressed in neurophysiological terms. The Kanizsa figure, shown in Figure 1 b, exemplifies this problem. The subjective experience of this illusion consists not only of the emergent collinear boundary, but the illusory triangle is perceived to be filled in perceptually with a uniform surface brightness that is perceived to be brighter than the white background of the figure. The subjective experience of the Kanizsa figure therefore can be depicted schematically as in Figure 1 c. Furthermore, the three pac-man features at the corners of the triangle are perceived as complete circles occluded by the foreground triangle, as suggested in Figure 1 d. There is considerable debate as to how this rich spatial percept is encoded neurophysiologically, and it has even been suggested (Dennett 1991, 1992, O'Regan 1992) that much of this perceptual information is encoded only implicitly, i.e. that the subjective percept is richer in information than the neurophysiological state that gives rise to that percept. However unless we invoke mystical processes beyond the bounds of science, every perceptual experience must correspond to specific neurophysiological processes or states, and the informational content of those neurophysiological states must be equivalent to the information content of the corresponding subjective experience, as proposed by Müller in the psychophysical postulate (Müller 1896, Boring 1933).
One way to circumvent this thorny issue is by proposing perceptual modeling as opposed to neural modeling, i.e. to model the information apparent in the subjective percept rather than the objective state of the physical mechanism of perception. In the case of the Kanizsa figure, for example, the objective of the perceptual model, given an input of the Kanizsa figure, is to generate a perceptual output image similar to Figure 1 c that expresses explicitly the properties observed subjectively in the percept. Whatever the neurophysiological mechanism that corresponds to this subjective experience, the information encoded in that physiological state must be equivalent to the information apparent in the subjective percept. Unlike a neural network model, the output of a perceptual model can be matched directly to psychophysical data, as well as to the subjective experience of perception. Although this is only an interim solution, for ultimately the neurophysiological basis of visual experience will also have to be identified, the value of the perceptual modeling approach is that it quantifies the informational content in subjective experience, which in turn sets a lower limit on the informational content that must be encoded in the corresponding neurophysiological state. This approach has proven successful in the past, especially in the field of color perception, where the explicit quantification of the information content of subjective color experience led directly to great advances in our understanding of the neurophysiological basis of color perception.
The perceptual modeling approach immediately reveals that the subjective percept contains more explicit spatial information than the visual stimulus on which it is based. In the Kanizsa triangle in Figure 1 b the triangular configuration is not only recognized as being present in the image, but that triangle is filled-in perceptually, producing visual edges in places where no edges are present in the input. Furthermore, the illusory triangle is filled-in with a white that is brighter than the white background of the figure. Finally, the figure produces a perceptual segmentation in depth, the three pac-man features appearing as complete circles, completing amodally behind an occluding white triangle. This figure demonstrates that the visual system performs a perceptual reification, i.e. a filling-in of a more complete and explicit perceptual entity based on a less complete visual input. The identification of this generative or constructive aspect of perception was one of the most significant achievements of Gestalt theory, and the implications of this concept have yet to be incorporated into computational models of perception.
The subjective percept of the Kanizsa figure contains more information than can be encoded in a single spatial image. For although the image of the explicit Kanizsa percept in Figure 1 c expresses the experience of the Kanizsa figure of Figure 1 b, a similar figure cannot be devised to express the experience of the camo-triangle in Figure 1 a, where the perceived contours carry no brightness information as do those in the Kanizsa figure. The perceptual reality of this invisible structure is suggested by the fact that this linear percept can be localized to the highest precision along its entire length, it is perceived to exist simultaneously along its entire length, and its spatial configuration is perceived to be the same across individuals independent of their past visual experience. Michotte (1964) refers to such percepts as amodal in the sense that they are not associated with any perceptual modality such as color, brightness, or stereo disparity, being seen only as an abstract grouping percept. And yet the amodal contour is perceived as a vivid spatial entity, and therefore a complete perceptual model would have to register the presence of such vivid amodal percepts with an explicit spatial representation. In a perceptual model this issue can be addressed by providing two distinct representational layers, one for the modal, and the other for the amodal component of the percept, as seen in Grossberg's Boundary Contour System / Feature Contour System (BCS / FCS) (Grossberg & Mingolla 1985, Grossberg & Todorovic 1988), where the FCS image represents the modal brightness percept, whereas the BCS image represents the amodal contour percept. The amodal contour image therefore represents the information captured by an outline sketch of a scene, which depicts edges of either contrast polarity as a linear contour in a contrast-independent representation. A full perceptual model of the experience of the Kanizsa figure therefore could be expressed by the two images of Figure 1 c and d, to express the modal and amodal components of the percept respectively. While the edges present in Figure 1 d are depicted as dark lines, these lines by definition represent invisible or amodal linear contours in the Kanizsa percept. Note that in this example the illusory sides of the Kanizsa figure register in both modal and amodal percepts, but the hidden portions of the black circles are perceived to complete amodally behind the occluding triangle in the absence of a corresponding perceived brightness contour. This kind of double representation can now express the experience of the camo triangle, whose modal component would correspond exactly to Figure 1 a, without any explicit brightness contour around the triangular figure, and an amodal component that would consist of a complete triangular outline, together with the multiple outlines of the visible fragments in the image.
There are several visual phenomena which suggest an intimate coupling between the modal and amodal components of the percept. Figure 2 a depicts three dots in a triangular configuration that generates an amodal triangular contour connecting the three dots. This grouping percept is entirely amodal, and it might be argued that there is no triangle present in this percept. And yet the figure is naturally described as a "triangle of dots", and the invisible connecting lines are localizable to the highest precision. Furthermore, the amodal triangle can be transformed into a modal percept, and thus rendered visible, as shown in Figure 2 b, where the three "v" features render the amodal grouping as a modal surface brightness percept. Figure 2 c demonstrates another transformation from an amodal to a modal percept. The boundary between the upper and middle segments of Figure 2 c are seen as an amodal grouping contour, devoid of any brightness component. When however the line spacing on either side of this contour is unequal, as in the boundary between the middle and lower portions of this figure, then the amodal contour becomes a modal one, separating regions of slightly different perceived brightness. Figure 2 d shows how the camo triangle can also be transformed into a modal percept by arranging for a different density of texture elements in the figure relative to the ground, producing a slight difference in surface brightness between figure and ground. These properties suggest that modal and amodal contours are different manifestations of the same underlying mechanism, the only difference between them being that the modal contours are made visible by features that provide a contrast difference across the contour.
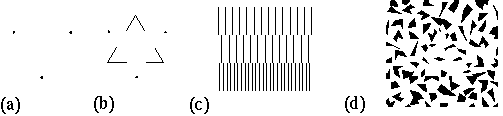
Figure 2. The relationship between modal and amodal perception in various illusory percepts. (a) An amodal triangular percept defined by dots at its three vertices becomes (b) a modal surface brightness percept with the addition of features that induce a contrast across the illusory contour. (c) An amodal (upper contour) and modal (lower contour) illusory edge percept, the brightness difference in the latter being due to a difference in line density across the contour. (d) The camo triangle can also be transformed into a modal percept by different density of fragments between figure and ground.
As the phenomena addressed by models of perception become increasingly complex, so too must the models designed to account for those phenomena, to the point that it becomes difficult to predict the response of a model to a stimulus without extensive computer simulations. In contrast to the neural network approach, the focus here will be on perceptual modeling, i.e. on the kinds of computation required to reproduce the observed properties of illusory figures without regard to issues of neural plausibility. In other words, the focus will be on the information processing manifest in perceptual phenomena, rather than on the neurophysiological mechanism of the visual system. Since illusory phenomena reveal spatial interactions between visual elements, perceptual processing will be expressed in terms of the equivalent image processing operations required to transform an input like the Kanizsa figure of Figure 1 b to explicit modal and amodal representations of the subjective experience of perception as suggested in Figure 1 c and d.
Figure 3 summarizes the computational architecture of the MLRF model. Figure 3 a depicts the surface brightness layer. Initially, this layer represents the pattern of luminance present in the visual stimulus. A process of image convolution transforms this surface representation into an edge representation that encodes only the brightness transitions at visual edges, but preserves the contrast polarity across those edges, resulting in a contrast-polarity-sensitive, or polar edge representation shown in figure 3 b. This operation represents a stage of abstraction, or reduction of image information to essential features. A further level of abstraction then drops the information of contrast polarity, resulting in a contrast-polarity-insensitive representation, or apolar edge layer, shown in figure 3 c. Next, a cooperative processing stage operates on both the polar and apolar edge images to produce polar and apolar cooperative edge layers, shown in Figure 3 d and e respectively. The feed-forward processing summarized so far is consistent with the conventional view of visual processing in terms of a hierarchy of feature detectors at different levels. I will then show how a reverse-transformation can be defined to reverse the flow of data in a top-down direction by the principle of reciprocal action, and this processing performs a reification, or reconstructive filling-in of information at the lower levels, based on the features present in the higher levels of the hierarchy. In the case of the Kanizsa stimulus, the effect of this top-down reification is to express back at the surface brightness level, those features that were detected at the higher levels of the hierarchy, such as the collinear alignment between the inducing edges. This reification reveals the general principle behind the appearance of the illusory triangle as a surface brightness percept.
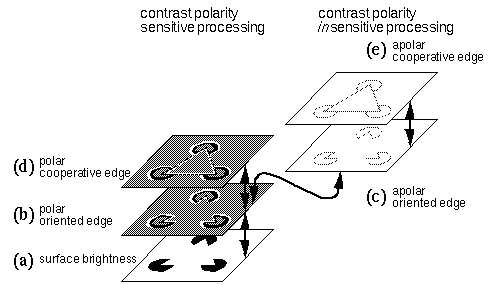
Figure 3.The Multi-Level Reciprocal Feedback model (MLRF) representational hierarchy. In feed-forward mode the processing proceeds upwards from the surface brightness image (a) through various levels of abstraction (b through e). At the highest levels (d and e) the illusory contour emerges. In top-down processing mode the features computed at higher levels are transformed layer by layer down to the lowest level (a) where they appear in the form of a surface brightness percept (not shown here, but as depicted in figure 1 c).
While image processing is defined in terms of quantized digital images and sequential processing stages, the model developed below is intended as a digital approximation to a parallel analog perceptual mechanism that is continuous in both space and time, as suggested by Gestalt theory. The field-like interactions between visual elements will be modeled with image convolution operations, where the convolution kernel represents a local field-like influence at every point in the image. The principle of emergence in perception will be modeled by an iterative algorithm that repeats the same sequence of processing stages until equilibrium is achieved. While the computer algorithm is only an approximation to the continuous system, the quantization in space and time, as well as the breakdown of a complex parallel process into discrete sequential stages, offers also a clear way of describing the component elements of a computational mechanism that operates as a continuous integrated whole.
The next section begins with a description of common image processing operations that are used in various neural network models to account for collinear illusory contour formation, with a focus on the spatial effects of each stage of processing, and how they relate to the observed properties of the percept. This presentation is intended partly as a tutorial for the benefit of those unfamiliar with the technicalities of image processing theory. Therefore the various processing stages are presented not only in mathematical form, but they are illustrated with graphical depictions of the actual results in order to demonstrate the effects of each stage of processing in easily understood intuitive terms. The mathematical and computational details are included only to provide exact specification, and are not essential to the larger message of the model. The technical details can therefore be safely ignored by those who are interested only in the more general principles that this model is designed to demonstrate. For clarity and historical consistency, the neural network terminology of cells and receptive fields will be used in the following discussion where appropriate to describe computational concepts inherited from the neural network modeling approach.
In image processing, edges are detected by convolution with a spatial kernel (Ballard & Brown, 1982), that operates like a template match between the image and the kernel. In the convolution process the kernel is effectively scanned across the image in a raster pattern, and at every spatial location, a measure of match is computed between the kernel and the underlying local region of the image. The output of this convolution is an image whose pixels represent this match measure at every spatial location in the original image. A template used for edge detection has the form of a local section of an edge, i.e. the kernel has positive and negative halves, separated by an edge at some orientation, representing a light / dark edge at that orientation, like the one shown in Figure 4 b. Such an edge detector produces a strong positive response wherever the template is passed over edges of the same light / dark polarity and orientation in the image, and a strong negative response is produced over edges of that same orientation but of the opposite contrast polarity. Over uniform regions, or over edges of orientations very different from that of the template, the response to the kernel is weak or zero. The output of this processing therefore is itself an image, of the same dimensions as the original image, except that the only features present in this image are regions of positive and negative values that correspond to detected edges in the original. This operation is also known as spatial filtering, because the kernel, or spatial filter, extracts from the input only those features that match the kernel. While the output of the convolution can be considered as a point by point result, the real significance of the output is seen in the spatial pattern of values in the output field.
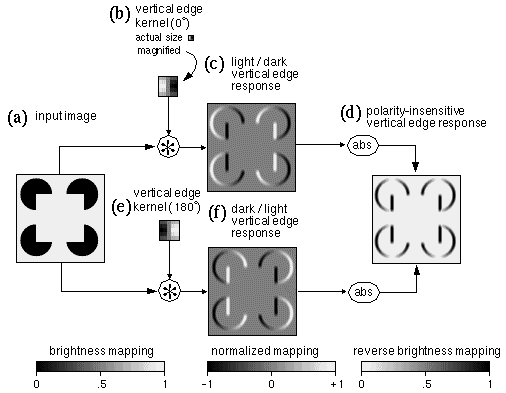
Spatial convolution or spatial filtering, using oriented edge kernels. The input image (a) is convolved with a vertical edge kernel (b or e) to produce a polar oriented edge representation (c or f) in which the original contrast polarity is preserved. Bright shades represent positive filter responses while dark shades represent negative responses, in a normalized mapping. An absolute value function transforms either (c) or (f) into an apolar edge image (d) depicted in reverse brightness mapping, i.e. positive values are depicted in dark shades, and zero values appear white.
Figure 4 illustrates the process of spatial filtering by image convolution. The input image shown in Figure 4 a represents the luminance profile of a Kanizsa figure composed of bright and dark regions. The convolution filter shown in Figure 4 b is a vertical edge detector of light / dark contrast polarity and of orientation 0°. This particular filter is defined by the sum of two Gaussian functions, one positive and one negative, displaced in opposite directions across the edge, as defined by the equation
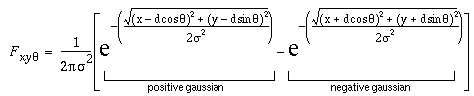
|
(EQ 1) |
[ Note for HTML version: If your browser does not load the "Symbol" font, the greek letters will not appear correctly in the text, Pi appears as p, theta appears as q, sigma appears as s etc. If you see proper greek letters here, this problem does not apply to you.]
where Fxy is the filter value at location (x,y) from the filter origin, q is the orientation of the edge measured clockwise from the vertical, and d is the displacement of each Gaussian across the edge on opposite sides of the origin. Kernels of this sort are generally balanced so that the filter values sum to zero, as is the practice in image processing to prevent the filtering process from adding a constant bias to the output image. In image processing, the spatial kernel is generally very much smaller than the image, in this case the filter used was 5 by 5 pixels. Figure 4 b shows this kernel both at actual size, i.e. depicted at the same scale as the input image, and magnified, where the quantization of the smooth Gaussian function into discrete pixels is apparent. The filter is displayed in normalized mapping, i.e. with negative values depicted in darker shades, positive values in lighter shades, and the neutral gray tone representing zero response to the filter.
The image convolution is defined by
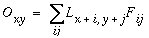
|
(EQ 2) |
where Oxy is the oriented edge response to the filter at location (x,y) in the image, (i,j) are the local displacements from that location, and Lx+i,y+j is the image luminance value at location (x+i,y+j). Figure 4 c shows the output of the convolution, again in normalized mapping. The vivid three-dimensional percept of raised surfaces observed in this image is spurious, and should be ignored. Note how the filter response is zero (neutral gray) within regions of uniform brightness in the original, both in uniform dark and bright areas. A positive response (bright contours) is observed in response to edges of the same light / dark contrast polarity as the filter, while a negative response (dark contours) occurs to edges of the opposite contrast polarity.
Figure 4 f shows the response to the same input by a vertical edge filter of orientation 80°, shown in Figure 4 e, and the output is the same as the response to the ° filter except with positive and negative regions reversed.
Often, the contrast polarity of edges is not required, for example a vertical edge might be registered the same whether it is of a light/dark or dark/light contrast polarity. In such cases an apolar edge representation can be used by applying an absolute value function to either Figure 4 c or f to produce the polar edge image shown in Figure 4 d, as defined by the equation
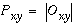
|
(EQ 3) |
For this image, a reverse-brightness mapping is used for display, i.e. the dark shades represent a strong response to vertical edges of either contrast polarity, and lighter or white shades represent weaker or zero response respectively. The reason for using the reverse mapping in this case, besides saving ink in a mostly zero-valued image, is because of nonlinearities in the printing process which make it easier to distinguish small differences in lighter tones than in darker tones. Since the focus of this paper is on illusory contours, the reverse mapping highlights these faint traces of low pixel values. Since illusory contour formation is often observed to occur even between edges of opposite contrast polarity, models of illusory contour formation often make use of this apolar oriented edge representation (Zucker et al. 1988, Hubel 1988, Grossberg & Mingolla 1985, Walters 1986).
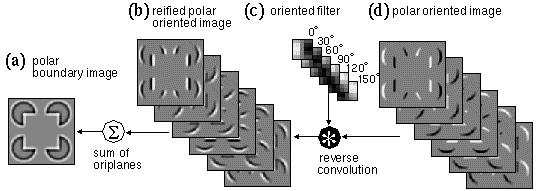
The image convolutions demonstrated in Figure 4 show only detection of vertically oriented edges. In order to detect edges of all orientations the image must be convolved with an array of spatial filters, encoding edges at a range of orientations. For example there might be twelve discrete orientations at 30 degree intervals, encoded by twelve convolution kernels. Convolving a single image with all twelve oriented kernels therefore produces a set of twelve oriented edge images, each of which has the dimensions of the original image. If the absolute value function is to be applied, only half of these convolutions need actually be performed. In much of the following discussion therefore, oriented edge filtering will be performed using six orientations at 30intervals from 0to 150 representing twelve polar orientations from 0to 330 Figure 5 depicts a set of convolutions of the Kanizsa image with a bank of oriented edge filters, followed by an absolute value function, to produce a bank of apolar oriented edge responses. The filter and the oriented response are three-dimensional data structures, with two spatial dimensions and a third dimension of orientation. The response of cells in the primary visual cortex has been described in terms of oriented edge convolution (Hubel 1988), where the convolution operation is supposedly performed by a neural receptive field, whose spatial pattern of excitatory and inhibitory regions match the positive / negative pattern of the convolution kernel. This data structure therefore is believed to approximate the information encoded by cells in the primary visual cortex. The utility of spatial filtering with a bank of oriented filters is demonstrated by the fact that most models of illusory contour formation are based on this same essential principle. For the three-dimensional data structure produced by oriented convolution contains the information required to establish collinearity in an easily calculable form, and therefore this data structure offers an excellent starting point for modeling the properties of the illusory contour formation process, both for neural network and for perceptual models. For convenience, the entire three-dimensional structure will be referred to as the oriented image, which is composed of discrete orientation planes, (henceforth contracted to oriplanes) one for each orientation of the spatial filter used. Figure 5 e shows a sum of all of the oriplanes in the apolar edge image of Figure 5 d, to show the information encoded in that data structure in a more intuitively meaningful form. In this oriplane summation, and in others shown later in the paper, a nonlinear saturation function of the form f(x) = x/(a+x) is applied to the summed image in order to squash the image values back down to the range 0 to 1 in the apolar layers, or from -1 to +1 in the polar cases, while preserving the low values that might be present in individual oriplanes.
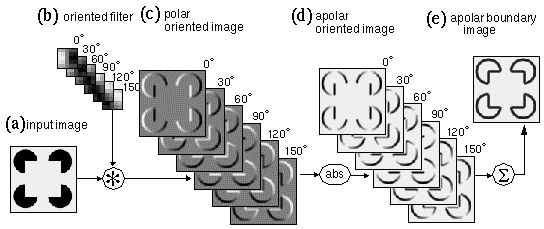
Oriented filtering of the Kanizsa figure (a) using filters through a full range of orientations (b) from 0° through 150° in 30° increments, producing a bank of polar oriented edge responses called collectively the polar oriented image (c). An absolute value function applied to that image produces an apolar oriented edge image (d). Summation across orientation planes and application of a nonlinear squashing function produces the apolar boundary image (e).
The different levels of the visual hierarchy express visual information in different forms. This facilitates computational operations tailored to that particular representation, with different types of computation being performed in each different representational level of the hierarchy. In a fully emergent system, feedback is not restricted to reciprocal transformations between representational levels, but also feedback computations performed within each individual level. In order to demonstrate this general principle in the specific example presented here, I will show how the oriented image representation offers a convenient format for a particular enhancement of that information, in this case by way of competition between the different oriplanes. Again, while this principle is demonstrated here in a specific example architecture, it is not that specific architecture, but the more general principle of emergence in a hierarchical representation that is being proposed here.
Examination of the curved portions of the pac-man figures in the oriented image in Figure 5 d reveals a certain redundancy, or overlap between oriplanes. This effect is emphasized in Figure 6 a, which shows just the upper-left pac-man figure for the first four oriplanes. Ideally, the vertical response should be strong only at the vertical portions of the curve, and fall off abruptly where the arc curves beyond 15 degrees, where the response of the 30 degree filter should begin to take over. Instead, we see a significant response in the vertical oriplane through about 60 degrees of the arc in either direction, and in fact, the vertical response only shows significant attenuation as the edge approaches 90 degrees in orientation. This represents a redundancy in the oriented representation or a duplication of identical information across the oriplanes. The cause of this spread of signal in the orientation dimension is limited sharpness in orientational tuning of the filter. One way to sharpen the orientational tuning is by elongating the oriented filter parallel to the edge in the kernel so as to sample a longer portion of the edge in the image. But this enhanced orientational tuning comes at the expense of spatial tuning, since such an elongated edge detector will produce an elongated response beyond the end of every edge in the image, i.e. there is a trade-off between spatial v.s. orientational tuning where an increase in one is balanced by a reduction in the other. The segregation of orientations in the oriented image offers an alternative means of sharpening the orientational tuning without compromising the spatial tuning. This is achieved by establishing a competition between oriplanes at every spatial location, as suggested by Grossberg & Mingolla (1985). The competition should not be absolute however, for example by preserving only the maximal response at any spatial location, because there are places in the image that legitimately represent multiple orientations through that point, for example at the corner of the square, where both horizontal and vertical edge responses should be allowed. A softer competition is expressed by the equation

|
(EQ 4) |

(a) Oriented competition demonstrated on the upper-left quadrant of the apolar oriented image from figure 5 a eliminates redundancy in the oriented representation (b), better partitioning the oriented information among the various orientation planes.
where Q represents the new value of the oriented image after the competition, the function pos() returns only the positive portion of its argument and zero otherwise, the function maxq() returns the maximum oriented response at location (x,y) across all orientations q, and the value v is a scaling factor that adjusts the stiffness of the competition. This equation is a static approximation to a more dynamic competition or lateral inhibition across different oriplanes at every spatial location, as suggested by Grossberg & Mingolla (1985). Figure 6 b shows the effects of this competition in reverse-brightness mapping mode, where the response of the vertical oriplane is now observed to fall off approximately where the 30 degree oriplane response picks up, so that the oriented information is now better partitioned between the different oriplanes. Figure 7 a shows the effect of oriented competition on the whole image. A similar oriented competition can be applied to the polar representation, producing the result shown in Figure 8 a.
The formation of illusory contours by collinearity, as exemplified in the Kanizsa figure, is observed to occur between edges that are 1: parallel, and 2: spatially aligned in the same direction as their common orientation, as long as 3: their spatial separation in that direction is not too great. The oriented image described above offers a representation in which collinearity can be easily calculated, for each oriplane of that structure is an image that represents exclusively edges of a particular orientation. Therefore all edge signals or active elements represented within a single oriplane fulfill the first requirement of collinearity, i.e. of being parallel to each other in orientation. The second and third requirements, being spatially aligned and nearby in the oriented direction, can also be readily calculated from this image by identifying regions of high value within an oriplane that are separated by a short distance in the direction of the corresponding orientation. For example in the vertical oriplane, a vertical illusory contour is likely to form between regions of high value that are related by a short vertical separation.
Collinearity in the oriented image can therefore be computed with another image convolution, this time using an elongated spatial kernel which Grossberg calls the cooperative filter, whose direction of elongation is matched to the orientation of the oriplane in question. An elongated kernel of this sort produces a maximal response when located on elongated features of the oriented image, which in turn correspond to extended edges in the input. It will also however produce a somewhat weaker response when straddling a gap in a broken or occluded edge in the oriented image. This filtering will therefore tend to link collinear edge fragments with a weaker boundary percept in the manner observed in the Kanizsa illusion and the camo triangle. If the magnitude of the filter value is made to decrease smoothly with distance from the center of the filter, this convolution will produce illusory contours whose strength is a function of the proximity between oriented edges, as is observed in the Kanizsa figure. The output of this stage of processing is called the cooperative image, and it has the same dimensions as the oriented image.
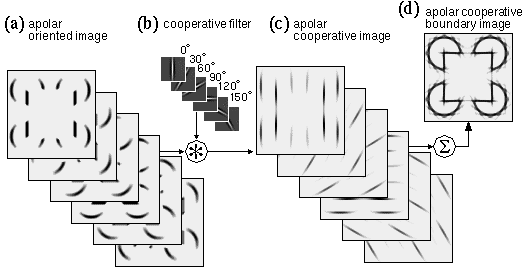
Cooperative filtering performed on the apolar oriented image (a) using a bank of cooperative filters (b) produces the apolar cooperative image (c) in which the illusory contour is observed to link collinear edge segments. The full illusory square can be seen by summing across orientation planes to produce the apolar cooperative boundary image (d).
Figure 7 illustrates cooperative processing of the oriented image, shown in Figure 7 a, using a cooperative convolution filter defined by
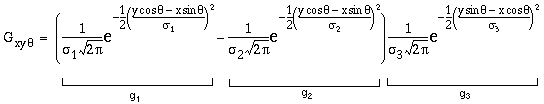
|
(EQ 5) |
This is a Gaussian function (g3) in the oriented direction (e.g. in the vertical direction for the vertical oriplane) modulated by a difference-of-Gaussians function (g1 - g2) in the orthogonal direction (e.g. in the horizontal direction for the vertical oriplane). Figure 7 b shows the shape of this convolution filter depicted in normalized mapping, i.e. with positive values depicted in lighter shades, and negative values in darker shades, with a neutral gray depicting zero values. A Gaussian profile in a spatial filter performs a blurring function, i.e. it spreads every point of the input image into a Gaussian function in the output. A difference-of-Gaussians on the other hand represents a sharpening, or deblurring filter as used in image processing, i.e. one that tends to invert a blur in the input, or amplify the difference between a pixel and its immediate neighbors. In this case, the cooperative filter performs a blurring in the oriented direction, and an image de-blurring or sharpening in the orthogonal direction. In these simulations the ratio s2 = 1.6 s1 was used for the difference-of-Gaussians as suggested by Marr (1982 p 63). The convolution is described by
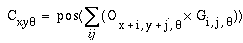
|
(EQ 6) |
where Cxyq is the response of the cooperative filter at image location (x,y) and orientation q. Note that in this convolution each oriplane of the oriented image is convolved with the corresponding oriplane of the cooperative filter to produce an oriplane of the cooperative image. The effect of this processing is to smear or blur the pattern from the oriented image in the oriented direction. For example the vertical oriplane of the oriented image, shown in Figure 7 a is convolved with the vertical plane of the cooperative filter, shown in Figure 7 b, to produce the vertical plane of the cooperative image, as shown in Figure 7 c. Notice how the lines of activation in the cooperative image are somewhat thinner than the corresponding lines in the oriented image, due to the sharpening effect of the negative side-lobes in the filter. This feature therefore serves to improve the spatial tuning of the oriented filtering of the previous processing stage, to produce the sharp clear contours observed in the Kanizsa illusion.
If cooperative filtering is to be performed in a single pass, the length of the cooperative filter must be sufficient to span the largest gap across which completion is to occur, in this case the distance between the pac-man inducers. The cooperative filter shown in Figure 7 b therefore is very much larger (35 x 35 pixels) than the oriented filter shown in Figure 5 b which was only 5 x 5 pixels, and in fact, Figure 7 b depicts the cooperative filter at the same scale as the input image, rather than magnified.The effect of this cooperative processing is shown in Figure 7 c, where every point of the oriented image is spread in the pattern of the cooperative filter. Note particularly the appearance of a faint vertical linking line between the vertical edges in the vertical cooperative oriplane, which demonstrates the most essential property of cooperative processing. Figure 7 d reveals the effects of this cooperative processing in more meaningful terms by summing the activation in all of the oriplanes of the cooperative image in Figure 7 c, showing the complete illusory square.
The boundary processing described above represents the amodal component of the percept, i.e. Figure 7 d should be compared with Figure 1 d. The vertical blurring of this signal in the cooperative layer can be seen as a field-like hypothesis building mechanism based on the statistical fact that the presence of an oriented edge at some location in the image is predictive of the presence of further parts of that same edge at the same orientation and displaced in the collinear direction, and the certainty of this spatial prediction decays with distance from the nearest detected edges. The cooperative processing of the whole image shown in Figure 7 d can therefore be viewed as a computation of the combined probability of all hypothesized edges based on actual edges detected in the image. That probability field is strongest where multiple edge hypotheses are superimposed, representing a cumulative or conjoint probability of the presence of edges inferred from those detected in the input.
While this processing does indeed perform the illusory completion, there are a number of additional artifacts observed in Figure 7 d. In the first place, the edges of the illusory square overshoot beyond the corners of the square. This effect is a consequence of the collinear nature of the processing, which is by its nature unsuited to representing corners, vertices, or abrupt line-endings, and a similar collinear overshoot is observed where the circumference of the pac-man feature intersects the side of the illusory square. Another prominent artifact is a star-shaped pattern around the curved perimeter of the pac-man features. This is due to the quantization of orientations in this example into 12 discrete directions (6 orientations), each oriplane of the cooperative filter attempting to extend a piece of the arc along a tangent to the arc at that orientation. These artifacts can be addressed with a more recurrent algorithm in which the cooperative processing is computed in an emergent manner, i.e. in multiple iterations to equilibrium, rather than in a single pass, as proposed in the Directed Diffusion model (Lehar 1994). However the details of that model are beyond the scope of the present paper, where the focus is not on the details of collinear illusory contour formation, but on the more general issue of how higher level global features such as collinear contours propagate their influence top-down to the lower levels of the visual representation, demonstrated in a system that is otherwise as simple as possible. With these reservations in mind, Figure 7 d demonstrates the principle of calculating a collinear illusory contour by convolution of the oriented image with an elongated cooperative filter. The computational mechanism of cooperative filtering of an oriented image representation therefore replicates some of the perceptual properties of illusory contour formation. Several models of illusory contours or illusory grouping percepts (Grossberg & Mingolla 1985, Walters 1986, Zucker et al. 1988, Parent & Zucker 1989) operate on this basic principle, although there is considerable variation in the details.
The hierarchical architecture revealed by neurophysiology suggests multiple parallel representations of the visual field in the visual cortex, each specialized to process certain types of visual information such as color, motion, binocular disparity, etc. In other words the hierarchy is not a strict linear arrangement of higher and lower level areas, but a more parallel architecture with multiple representations within each hierarchical level. The effects of these different visual maps however is to produce a single coherent visual experience that includes aspects of color, motion, binocular disparity, etc. The emergence proposed by Gestalt theory would suggest that these different representational maps should be coupled together to define a single system in which computations performed in one map have an immediate influence on the representation in all of the other maps. The principle behind this coupling between different representational maps will be demonstrated here with the introduction of a polar boundary processing stream, that runs parallel to the apolar processing stream developed above.
Grossberg & Mingolla (1985) suggest that cooperative filtering occurs in an apolar oriented edge representation, in order to allow collinear completion to occur between edges of opposite direction of contrast, as is observed in the camo-triangle of Figure 1 a. However in the case of the Kanizsa figure, the surface brightness percept preserves the direction of contrast of the inducing edges, which suggests that the edge signal that propagates between the inducers can carry contrast information when it is available, although the amodal completion is also observed along edges of alternating contrast polarity, as observed in the camo triangle. Polar collinear boundary completion can be computed very easily from the polar oriented edge representation depicted in Figure 5 c by performing cooperative filtering exclusively on the positive values of the polar oriented edge image, producing a polar cooperative response from 0° through 150°, and then again exclusively on the negative values of the polar image producing the polar cooperative response from 180° through 330°. Therefore the polar cooperative image must have twice as many oriplanes as the apolar representation to accommodate the two directions of contrast for each orientation. Alternatively, as with the polar oriented representation itself, the polar cooperative image can be encoded in both positive and negative values, the former representing collinear edges of one contrast polarity, while the latter represents the opposite contrast polarity, with both positive and negative values expressed in a single image. This compression is valid because the two contrast polarities are mutually exclusive for any particular location on an edge.
Figure 8 demonstrates polar collinear boundary completion by convolution of the polar oriented edge image in Figure 8 a with the cooperative filter shown in Figure 8 b. Figure 8 c shows the polar cooperative response, where the positive (light shaded) regions denote cooperative edges of dark/light polarity, and the negative (dark shaded) regions of Figure 8 c denote cooperative edges of light/dark polarity, using the same polarity encoding as seen in Figure 8 a. Figure 8 d shows the sum of the oriplanes in Figure 8 c to demonstrate intuitively the nature of the information encoded in the oriplanes of Figure 8 c. Note the emerging illusory contours in this figure, with a dark-shaded i.e. negative contrast edge on the left side of the square, and a light-shaded positive contrast edge on the right side of the square reflecting the opposite contrast polarities.
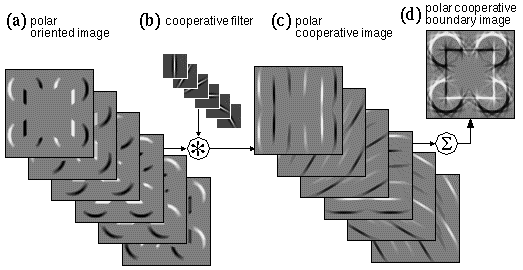
Cooperative filtering as in figure 7, this time performed on the polar oriented edge image (a) using the same cooperative filters (b) to produce the polar cooperative image (c). The full illusory figure is seen by summing across orientation planes to produce the polar cooperative boundary image (d). Positive values (light shading)correspond to light/dark transitions in the original, whereas negative values (dark shading) represent dark/light transitions.
The principle of emergence is easy enough to define in a parallel architecture, where various parallel elements in the system have a mutual influence on each other within a single representational code. This was demonstrated in the competition between oriplanes described above, where the various oriplanes of the oriented image inhibit each other reciprocally at each spatial location. The concept is more elusive however in a hierarchical architecture with different representational codes at different levels, especially when information is lost or abstracted in the bottom-up processing. This was demonstrated in the architecture developed above, where a spatial convolution compresses a complex spatial match to a single match value at every pixel location. For example there are many different combinations of pixels at a particular region in the surface brightness image that would all produce the same polar oriented edge response at that location. Higher up in the apolar level that number of combinations is doubled, since the direction of contrast information is lost or abstracted in order to produce invariance to contrast polarity. Likewise, there are many combinations of activations in the oriented image that all produce the same higher level polar cooperative response, and even more for the apolar cooperative response.
The general principle proposed here is that the top-down processing between representational levels performs a kind of inversion of the corresponding bottom-up processing stream between those same levels. The effect is to "print" an idealized exemplar of the higher level feature back at the lower level, producing at the lower level a perfect copy of the feature that was detected at the higher level, but expressed in the appropriate representational format of the lower level of the hierarchy. In other words the bottom-up processing serves to recognize features present in the visual field, as suggested in the conventional feature-detector concept of visual processing, and the top-down processing serves to reconstruct a high resolution reified visual scene that is consistent with the higher level features detected in that scene. This is exactly the concept suggested by illusions like the Kanizsa figure, where the illusory triangle is observed as a low-level reified visual experience that is consistent with the triangular occluding form recognized in that figure. While a single high level feature corresponds to a great variety of possible lower-level features, the various interactions across the visual hierarchy and within the individual representational levels act in conjunction with the pattern present in the visual input, to produce a final perceptual state that represents the best guess or optimal reconstruction of the visual input. That reconstruction, or perceptual interpretation of the visual input is not manifest only at the top, or the bottom of the visual hierarchy, but at every level of the hierarchy simultaneously, with each level of the hierarchy contributing its own influence on the final perceptual state. This principle represents the central concept of the present proposal as a means to resolve the apparantly contradictory concepts of reciprocal feedback with the concept of a hierarchical architecture.
Lehar & Worth (1991) propose a complementary process to the computation of image convolution in the form of a reverse convolution, which is a literal reversal of the flow of data through the convolution filter, as suggested by the Gestalt principle of reciprocal action. In the forward convolution of oriented filtering defined in Equation 2, the single output value of the oriented edge pixel Oxy is calculated as the sum of a region of pixels in the input luminance image Lx+i,y+j, each multiplied by the corresponding filter value Fij, as suggested schematically in Figure 9 a. In the reverse convolution a region of the reified oriented image Rx+i,y+j, is calculated from a single oriented edge response Oxy which is passed backwards through the oriented filter Fij as defined by the equation
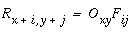
|
(EQ 7) |
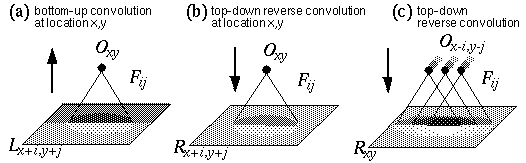
Forward and reverse convolution. In the forward convolution (a) a single oriented edge response is computed from a region of the input luminance image as sampled by the oriented filter. In reverse convolution (b) that single oriented response is used to generate a "footprint" of the original oriented filter "printed" on the reified image, modulated by the sign and magnitude of the oriented response, i.e. a negative oriented response produce a negative (reverse contrast) imprint of the filter on the reified image. Footprints from adjacent oriented responses overlap on the reified oriented image (c).
This equation defines the effect of a single oriented edge response on a region of the reified image, which is to generate a complete "footprint" in the reified image in the shape of the original oriented filter used in the forward convolution as suggested schematically in Figure 9 b. The contrast of the footprint is scaled by the magnitude of the oriented response at that point, and if the oriented response is negative, then the footprint is negative also, i.e. a negative light/dark edge filter is printed top-down as a reverse contrast dark/light footprint. Any single point Rxy in the reified image receives input from a number of neighboring oriented cells whose projective fields overlap on to that point, as suggested schematically in Figure 9 c. The reified oriented image therefore is calculated as
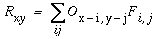
|
(EQ 8) |
or equivalently,
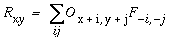
|
(EQ 9) |
It turns out therefore that the reverse convolution is mathematically equivalent to a forward convolution performed through a filter that is a mirror image of the original forward filter, reflected in both x and y dimensions, i.e. F'ij = F-i,-j.
Figure 10 demonstrates a reverse-convolution of the polar oriented edge image, shown in Figure 10 d, back through the same oriented filter, shown in Figure 10 c by which it was originally generated, to produce the reified polar edge image, whose individual oriplanes are shown in Figure 10 b. Note how lines of positive value (light shades) in Figure 10 d become light/dark edges in Figure 10 b, while lines of negative values (dark shades) in Figure 10 d become edges of dark/light polarity in Figure 10 b. Since in the forward convolution one image was expanded into six orientation planes, in the reverse convolution the six planes are collapsed back into a single two-dimensional image by summation, as shown in Figure 10 a. Note that the reverse convolution is not the inverse of the forward convolution in the strict mathematical sense, since the reified oriented image is still an edge image rather than a surface brightness representation. This image does however represent the information that was extracted or filtered from the original image by the process of oriented filtering, but that information is now translated back to terms of surface brightness rather than of orientation, i.e. the regions of positive (light) and negative (dark) values in Figure 10 a represent actual light and dark brightness in the original image. The reason why this reified image registers only relative contrast across boundaries in the original, rather than absolute brightness values within uniform regions, is exactly because the process of oriented filtering discards absolute value information, and registers only contrast across boundaries. The reified oriented image is very similar in appearance to the image produced by convolving the original with a circular-symmetric difference-of-Gaussians filter, or equivalently, a band-pass Fourier filtering of the original. The two-dimensional polar image shown in Figure 10 a will be referred to as the polar boundary image.
Reverse convolution of the oriented image (d) back through the original oriented filter (c) produces the reified polar oriented image (b) in which negative oriented edges become dark/bright contrast edges, whereas positive oriented edges become bright/dark contrast edges. A summation across orientation planes (a) produces the polar boundary image which represents the spatial information extracted from the original image by the oriented filtering.
Grossberg &Todorovic (1988) suggest that the surface brightness information that is lost in the process of image convolution can be recovered by a diffusion algorithm that operates by allowing the brightness and darkness signals in the polar boundary image of Figure 10 a to diffuse outward spatially from the boundaries, in order to fill in the regions bounded by those edges with a percept of uniform surface brightness. For example the darkness signal seen along the inner perimeter of each of the four pac-man features in Figure 10 a should be free to diffuse spatially within the perimeter of those features, to produce a percept of uniform darkness within those features, as shown in Figure 11 c, while the brightness signal at the outer perimeter should be free to diffuse outwards, to produce a percept of uniform brightness between the pac-man features, as shown also in Figure 11 c. The diffusing brightness and darkness signals however are not free to diffuse across the boundaries in the image, as defined for example by the apolar boundary image shown in Figure 11 b, which was computed as the sum of oriplanes of the apolar oriented edge image, as shown also in Figure 5 e. In other words the spatial diffusion of the brightness and darkness signals is bounded or confined by the apolar boundary signal, which segments the image into disconnected regions, within each of which the perceived brightness will tend to become uniform by diffusion, just as water within a confined vessel tends to seek its own level.
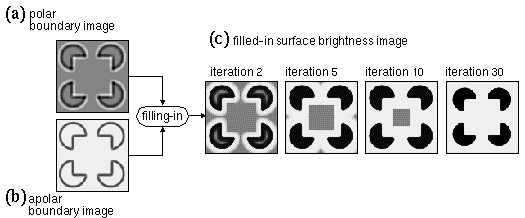
Surface brightness filling-in uses the polar boundary image (a) as the source of the diffusing brightness (and darkness) signal, the diffusion being bounded by the boundaries in the apolar boundary image (b). Successive stages of the diffusion are shown (c) to demonstrate how the brightness and darkness signals propagate outwards from the polar edges to fill in the full surface brightness percept.
The equation for this diffusion is derived from Grossberg's FCS model (Grossberg & Todorovic 1988), again simplified somewhat as a consequence of being a perceptual model rather than a neural model, and thereby being liberated from the constraints of "neural plausibility". The diffusion is given by
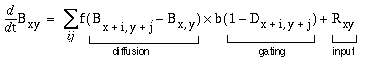
|
(EQ 10) |
where Bxy is the perceived brightness at location (x,y), which is driven by the diffusion from neighboring brightness values within the immediate local neighborhood (i,j), which in turn is proportional to the total difference in brightness level between the pixel and each of its local neighbors. A brightness pixel surrounded by higher valued neighbors will therefore grow in brightness, while one surrounded by lower valued neighbors will decline in brightness. This diffusion however is gated by the gating term, which is a function of the strength of the boundary signal Dxy at location (x,y), i.e. the gating term goes to zero as the boundary strength approaches its maximal value of +1, which in turn blocks diffusion across that point. The diffusion and the gating terms are further modulated by the diffusion or flow constant f, and the gating or blocking constant b respectively. Finally, the flow is also a function of the input brightness signal Rxy from the reified oriented image at location (x,y), which represents the original source of the diffusing brightness signal, and can be positive or negative to represent bright or dark values respectively. The computer simulations, which are otherwise intolerably slow, can be greatly accelerated by solving at equilibrium, i.e. in each iteration, each pixel takes on the average value of its eight immediate neighbors, weighted by the boundary strength at each neighboring pixel, so that neighboring pixels located on a strong boundary contribute little or nothing to the weighted average. This is expressed by the equilibrium diffusion equation
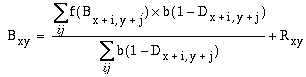
|
(EQ 11) |
where Bxy on the left side of the equation represents the new value calculated from the previous brightness value Bxy on the right side of the equation. Figure 11 c shows the process of diffusion after 2, 5, 10, and 30 iterations of the diffusion simulation, showing how the diffusing brightness signal tends to flood enclosed boundaries with a uniform brightness or darkness percept.
The example of forward and reverse processing represented in Figures 5, 10 and 11 is not a very interesting case, since the reified brightness percept of Figure 11 c is essentially identical in form to the input image in Figures 5 a, showing just the input stimulus devoid of any illusory components. However even in its present form the model explains some aspects of brightness perception, in particular the phenomena of brightness constancy (Spillmann & Werner 1990 p. 131) and the simultaneous contrast illusion (Spillmann & Werner 1990 p. 131), as well as the Craik-O'Brien-Cornsweet illusion (Spillmann & Werner 1990 p. 136). Brightness constancy is explained by the fact that the surface brightness percept is reified from the relative brightness across image edges, and therefore the reified brightness percept ignores any brightness component that is uniform across the edges. The effect is a tendency to "discount the illuminant", i.e. to register the intrinsic surface reflectance of an object independent of the strength of illumination. Figure 12 demonstrates this effect using exactly the same forward and reverse processing described above, this time applied to a Kanizsa figure shown in Figure 12 a to which an artificial illuminant has been added in the form of a Gaussian illumination profile that is combined multiplicatively with the original Kanizsa stimulus, as if viewed under a non-uniform illumination source. Figure 12 b shows the polar boundary image due to this stimulus, showing how the unequal illumination of the original produces minimal effects in the oriented edge response. Consequently the filled-in surface brightness percept shown in Figure 12 d is virtually identical to that in Figure 11 c thus demonstrating a discounting of the illuminant in the surface brightness percept. In essence, the principle expressed by this model is a spatial integral (the diffusion operation) applied to a spatial derivative (the edge convolution) of the luminance image, and several models of brightness perception (Arend & Goldstein 1981, Land & McCann 1971, Grossberg & Todorovic 1988) have been proposed on this principle as the basis of brightness constancy.
The phenomenon of lightness constancy, or discounting of the illuminant is demonstrated using the same forward and reverse processing.(a) A Gaussian illumination profile is added synthetically to the Kanizsa figure. The polar (b) and apolar (c) boundary images show little evidence of the unequal illumination in (a), and therefore the filled-in surface brightness image (d) is restored independent of that illuminant.
Figure 13 demonstrates the brightness contrast illusion using the same forward and reverse processing described above. Figure 13 a shows the stimulus, in which a gray square on a dark background appears brighter perceptually than the same shade of gray on a bright background. Figure 13 b shows the reified polar edge image, revealing a bright inner perimeter for the left hand square, and a dark inner perimeter for the right hand square, due to the contrast with the surrounding background. Figure 13 c shows the apolar boundary image, and Figure 13 d shows the filled-in surface brightness percept, which is consistent with the illusory effect, i.e. the square on a dark background is reified perceptually as brighter than the square on the bright background.

The Brightness Contrast Illusion (a) produces different polar boundary responses (b) in the inner perimeter of the two gray squares, which in turn produces different surface brightness percepts in the filled-in image (d).
Figure 14 demonstrates the Craik-O'Brien-Cornsweet illusion, again using the same forward and reverse processing described above. Figure 14 a shows the stimulus, which is a uniform gray with a brightness "cusp" at the center, i.e. from left to right, the mid gray fades gradually to dark gray, then jumps abruptly to white, before fading gently back to mid gray in the right half of the figure. The percept of this stimulus is of a uniformly darker gray throughout the left half of the figure, and a lighter gray throughout the right half. If the cusp feature is covered with a pencil, the neutral gray of the stimulus will be seen. This illusion offers further evidence that the perception of surface brightness depends on the edges, or brightness transitions in the stimulus, which promote a diffusion of brightness signal throughout the regions separated by those transitions. The filled-in surface brightness image shown in Figure 14 d shows how this effect too is replicated by the model.
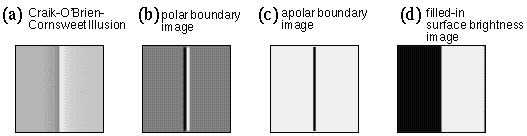
The Craik-O'Brien-Cornsweet Illusion (a) produces a polar (b) and apolar (c) image, from which the brightness diffusion reconstructs regions of different brightness (d).
The regions of darker and lighter gray produced in this simulation, and the previous brightness contrast simulation appear much exaggerated relative to the subtle difference in tone observed subjectively. In the first place these illusions are somewhat dependent on spatial scale, for example the brightness contrast effect is more extreme when viewing a tiny gray patch against a white or black background. Furthermore, the simulations presented here are intended to demonstrate the computational principles active in perception, rather than the exact parametric balance to produce the proper brightness percept for all of the phenomena modeled.
The effects of the illusory contours, absent from the filled-in percept of Figure 11 c, can be added to the simulation by simply coupling the cooperative layers into the feedback loop, as explained below. Figure 15 c shows the polar cooperative image computed by feed-forward convolution, as shown also in Figure 8. A reverse convolution back through the same cooperative filter transforms this cooperative representation back to a reified cooperative representation in the oriented edge layer, as shown in Figure 15 b. Due to the symmetry of the cooperative filter, this image is not very different from the original cooperative image, being equivalent to a second pass of forward convolution with the cooperative filter, which simply amplifies the spreading in the oriented direction, and the thinning in the orthogonal direction. Next, a reverse-convolution is performed on this oriented edge image through the original oriented filter to produce a reified oriented image as shown in figure 15 a, this time complete with faint traces of the polar illusory contour linking the inducing edges. A summing of the oriplanes of this image produces the polar boundary image with cooperative influence. At the same time, a similar reification is performed in the apolar data stream, to produce the apolar boundary image with cooperative influence, shown in Figure 16 b. Finally, a surface brightness filling-in is performed using these two boundary images to produce the final modal percept which is shown in Figure 16 c. Note how the disturbing star-shaped artifacts apparent in Figure 16 b are much diminished in the corresponding surface brightness percept in Figure 16 c because they do not define enclosed contours, and therefore any brightness difference across these open-ended contours tends to cancel by diffusion around the open end. However where these extraneous contours do form closed contours, they block the diffusion of brightness signal and produce artifacts. This can be seen for example on both sides of the illusory edge of the square in Figure 16 b where the extraneous contours from the adjacent pac-man figures from opposite sides intersect, and thereby capture the diffusion of the darkness signal from diffusing smoothly into the background portion of the figure, resulting in a local concentration of darkness just outside of the illusory contour in Figure 16 c. Similarly, extraneous contours inside the illusory square block the diffusion of brightness signal from filling-in uniformly within the illusory square. Figure 16 d, e, and f demonstrate the same filling-in operation except this time using polar and apolar cooperative images computed by the Directed Diffusion algorithm (Lehar 1994) in which the extraneous contours are much reduced, resulting in a more veridical filling-in result. Although the details of the Directed Diffusion algorithm are beyond the scope of the present paper, the principles of perceptual completion of the Kanizsa figure by top-down feedback through a hierarchical representation are clearly demonstrated in this figure.

Feedback from the polar cooperative layer (c) is achieved by reverse convolution through the cooperative filter to produce the reified polar cooperative image (b, at the oriented image level), from whence a reverse convolution through the oriented filter produces the reified oriented image (a). Since the forward oriented convolution involves an expansion from one oriplane to six, the reverse convolution actually collapses back to the single plane of the surface brightness layer by summation across oriplanes to produce the polar boundary image with cooperative influence.
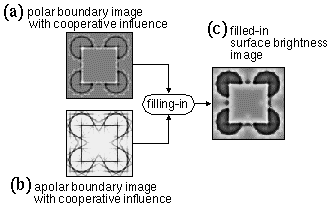
After cooperative feedback, the polar and apolar boundary images (a and b) contain traces of the collinear illusory contour. Therefore a surface brightness filling-in from these images (c) should generate the illusory percept as suggested in figure 1 (c). However in this case extraneous boundary signals interfere with the diffusion of brightness signal resulting in an irregular brightness distribution. Nevertheless, the principle behind the emergence of the illusory figure is clear. The problem of extraneous edges will be addressed by refinement of the cooperative processing model.
While the modeling presented above accounts for the formation of modal illusory percepts, the same model also accounts for amodal illusory grouping by producing a grouping edge in the apolar cooperative image which however produces no effect back down at the image level, because there is no contrast signal available across the contour to generate the brightness percept. Figure 17 a shows a stimulus similar to figure 2 c, and similar in principle to the camo triangle in figure 1 a. Figure 17 b shows the polar boundary image with cooperative influence, showing how the amodal contour is completed between the line endings, to produce a collinear grouping percept. The cooperative processing in the polar data stream on the other hand does not complete the same illusory contour because the contrast reversals between alternate edge stimuli cancel, as seen in the polar boundary image shown in Figure 17 c. This stimulus can however be transformed into a modal percept by arranging for a different density across the contour, as shown with the modal camo triangle in figure 2 c. Figure 17 d shows this kind of a stimulus, which produces the same kind of amodal grouping percept, as seen in the apolar boundary image in Figure 17 e, however the average contrast polarity across this contour now produces a weak horizontal polar boundary, as shown in Figure 17 f, and this polar boundary will feed the brightness diffusion to produce a difference in surface brightness in the percept across that contour.
Amodal illusory contour formation is demonstrated for a stimulus (a) with alternating contrast polarity across the illusory contour. The salience of this contour is registered by a strong apolar boundary signal (b) along the illusory edge. However the contrast reversals along that edge preclude a polar boundary response (c). When the ratio of dark and bright regions across the contour are unequal (d), this still produces a strong amodal boundary response (e) but it now also provides a weak polar cooperative response (f) along the illusory contour, which in turn leads to a difference in perceived surface brightness across the contour, as seen in the illusions of figure 2 c and d.
The hierarchical architecture depicted in Figure 3 extends upwards only to the cooperative representation. However the human visual system surely extends to much higher representational levels, including completion of vertices defined by combinations of edges, completion of whole geometrical forms such as squares and triangles defined by combinations of vertices, and completion of whole compound forms composed of configurations of simpler geometrical forms. The general implications of the MLRF model are that these higher featural levels would be connected to the lower levels with bidirectional connections, in the same manner as the connections between the various lower levels of the featural hierarchy described above. Therefore as higher order patterns are detected at the higher levels, this detection in turn would be fed top-down to the lower levels, where they would serve to complete the detected forms back at the lowest levels of the representation, resulting in a high-resolution rendition of those features at the surface brightness level. It is this reification of higher order features that explains how global properties such as figural simplicity, symmetry, and closure can influence the low-level properties of the percept such as the salience of the amodal contour of the camo triangle of figure 1 a, and the contrast across the modal contours of the modal camo triangle in figure 2 d.
I have presented a detailed computational model of visual processing, some of which bears resemblance to a number of neural network models of vision. However the intent here is more general for it is not the details of the model that are at issue here, but rather the more general computational principle that that model demonstrates by example. What I propose is not so much a model of visual processing, as it is a paradigm, or general way of conceptualizing models of vision that allows the concept of a hierarchical visual representation built of heterogeneous representational levels to be resolved with the notion of emergence and feedback suggested by Gestalt theory, using the principle of reciprocal action. A principal focus of the present paper has been on the issue of invariance in perception, and how that invariance involves an abstraction, or reduction of information content in the bottom-up processing up the visual hierarchy. This in turn suggests a reification, the inverse of abstraction, as a property of the top-down processing stream, in order to restore the information that was lost in the bottom-up processing.
The notion of feedback in models of vision is itself not new, and has been proposed by various authors to account for emergence and reification in vision (Grossberg & Mingolla 1985, Zucker et al. 1988). The notion of perceptual filling-in as an explicit computational operation is also not new in the literature of computational models of vision (Grossberg & Mingolla 1985, Grossberg & Todorovic 1988, Zucker et al. 1988). What is new in the present proposal is the connection between perceptual filling-in and top-down feedback in the visual hierarchy. While the BCS model (Grossberg & Mingolla 1985) performs a similar collinear boundary completion, with top-down feedback to the lower level local edge detectors, the feedback in that model is not presented as an inverse transformation of the feed-forward process of collinear edge detection. While the FCS model (Grossberg & Todorovicz 1988) incorporates a brightness diffusion mechanism to account for surface brightness filling-in as in the Kanizsa figure, that mechanism was not presented as an inverse transformation of the feed-forward process of oriented edge detection. Instead, those mechanisms were presented as specific computational strategies employed to account for specific illusory phenomena. The present proposal is more general, for it suggests a general strategy of information processing in biological vision by way of reciprocal and quasi-inverse feed-forward and feedback pathways, which can therefore apply to any other processing at higher levels of the visual hierarchy. The implications of this view of visual processing are that the computations performed at each level of the visual hierarchy are not so much a matter of processing the data flowing through them, as suggested by a feed-forward computer algorithmic view, but rather the effects of processing in any layer modulates the representation at every other level of the system simultaneously. This was seen for example in the simulations described above, where the coupling of the cooperative level into the feedback loop subtly altered the patterns of activation at all other levels simultaneously, enhancing specifically those features in the input which correspond to a cooperative edge. This behavior is comparable to the properties observed in analog circuits, in which the addition of extra capacitors or inductors at various points in a circuit subtly alters the behavior of the circuit as a whole as measured at any other point in the circuit, not only within or "beyond" the added component as suggested by a feed-forward paradigm.
It is this general principle of perceptual processing that accounts in general terms for many of the illusory phenomena observed in Gestalt illusions. It explains why the multiple fragmented edges of the camo triangle stimulus produce not only a recognition of a triangular configuration, but also an amodal edge percept around the perimeter of the perceived triangle that is continuous across the gaps, and that percept is experienced at the highest perceptual resolution. It explains why the pac-man features at the corners of the Kanizsa triangle produce not only a triangular recognition, but also a percept of linear edges that span the gap between the stimulus edges to complete the triangular form, and an experience of the triangular surface as a continuous filled-in surface brightness percept. It explains why a contrast across a visual edge in the Craik-O'Brien Cornsweet illusion creates a filled-in surface brightness percept on either side of that contour. More generally, this paradigm of visual processing offers an explanation for the generative or constructive aspect of perception identified by Gestalt theory, as manifest in the many and various filling-in and completion phenomena observed in Gestalt illusions.
This same general principle of emergence in a hierarchical visual representation accounts also for the unity of conscious experience. For the world we perceive to surround us is not experienced as an assembly of disconnected features, or as separate images of color, motion, binocular disparity etc. as suggested by the fragmented architecture of the visual cortex, but as a single coherent spatial percept in which color, motion, and binocular disparity are perceived to be superimposed and integrated in the various objects of the perceptual world. The fact that the various components of the percept are experienced as superimposed is explained by the fact that the different representational levels of the hierarchy represent the same visual space. For example a location (x,y) in the apolar cooperative image maps to the same point in visual space as the location (x,y) in the surface brightness image, although the nature of the perceptual experience represented in those levels is different. The subjective experience of the final percept therefore corresponds not only to the state of the highest levels of the representation as suggested by the feed-forward approach, but rather, all levels are experienced simultaneously as components of the same perceptual experience superimposed in visual space, as suggested by the separate modal and amodal components of the Kanizsa figure depicted in Figure 1 c and d. This approach to modeling perception does not resolve the most central issue of consciousness, i.e. it does not explain how a particular pattern of energy in the visual system becomes a subjective conscious experience. However this approach circumvents that thorny issue by simply registering the different aspects of the conscious experience at different levels in an isomorphic representation, expressed in perceptual modeling, rather than neurophysiological terms. Therefore the patterns of energy in the various levels of the model can be matched directly to a subject's report of their spatial experience, whether the subject describes a perceived surface brightness, a perceived contrast across an edge, or an amodal grouping percept. Unlike a neural network model therefore, the output of the model can be matched directly to psychophysical data independent of any assumptions about the mapping from neurophysiological to perceptual variables. This model of visual computation therefore offers a paradigm that resolves the fragmented and hierarchical processing architecture revealed in neurophysiological studies with the global unity and coherence of the visual world revealed by Gestalt theory.
Arend L., & Goldstein R. 1987 "Lightness Models, Gradient Illusions, and Curl". Perception & Psychophysics 42 (1) 65-80.
Ballard D. H. & Brown C. M. 1982 "Computer Vision". Prentice-Hall, Englewood Cliffs, NJ.
Boring 1933 "The Physical Dimensions of Consciousness". New York: Century.
Coren S., Ward L. M., & Enns J. J. 1979 "Sensation and Perception". Ft Worth TX, Harcourt Brace.
Dennett D. 1991 "Consciousness Explained". Boston, Little Brown & Co.
Dennett D. 1992 "`Filling In' Versus Finding Out: a ubiquitous confusion in cognitive science". In Cognition: Conceptual and Methodological Issues, Eds. H. L. Pick, Jr., P. van den Broek, & D. C. Knill. Washington DC.: American Psychological Association.
Grossberg S, Mingolla E, 1985 "Neural Dynamics of Form Perception: Boundary Completion, Illusory Figures, and Neon Color Spreading" Psychological Review 92 173-211.
Grossberg S, Todorovic D, 1988 "Neural Dynamics of 1-D and 2-D Brightness Perception: A Unified Model of Classical and Recent Phenomena" Perception and Psychophysics 43, 241-277.
Hubel D. H. 1988 "Eye, Brain, and Vision". New York, Scientific American Library.
Koffka K. 1935 "Principles of Gestalt Psychology". New York, Harcourt BraceI.
Köhler W. 1920 "Die physichen Gestalten in Ruhe und im stationären Zustand. Berlin: Braunschweig.
Land E. H. & McCann J. J. 1971 "Lightness and Retinex Theory". Journal of the Optical Society of America 61 1-11.
Lehar S. 1994 "Directed Diffusion and Orientational Harmonics: Neural Network Models of Long-Range Boundary Completion through Short-Range Interactions". Ph.D. Thesis, Boston University. *Note* apply to author for uncensored version of the thesis.
Lehar S. & Worth A. 1991 "Multi-resonant boundary contour system" Boston University, Center for Adaptive Systems technical report CAS/CNS-TR-91-017.
Marr D, 1982 "Vision". New York, W. H. Freeman.
Michotte A., Thinés G., & Crabbé G. 1964 "Les complements amodaux des structures perceptives". Studia Psychologica. Lovain: Publications Universitaires. In Michotte's Experimental Phenomenology of Perception, G. Thinés, A. Costall, & G. Butterworth (eds.) 1991, Lawrence Erlbaum, Hillsdale NJ.
Müller G. E. 1896 "Zur Psychophysik der Gesichtsempfindungen". Zts. f. Psych. 10.
O'Regan, K. J., 1992 "Solving the `Real' Mysteries of Visual Perception: The World as an Outside Memory" Canadian Journal of Psychology 46 461-488.
Parent P. & Zucker S. W. 1989 "Trace Inference, Curvature Consistency, and Curve Detection". IEEE Transactions on Pattern Analysis & Machine Intelligence II (8).
Spillmann L. & Werner J. S. 1990 "Visual Perception- the Neurophysiological Foundations". Academic Press Inc. San Diego.
Walters, D. K. W. 1986 "A Computer Vision Model Based on Psychophysical Experiments in Pattern Recognition by Humans and Machines", H. C. Nusbaum (Ed.), Academic Press, New York.
Zucker S. W., David C., Dobbins A., & Iverson L. 1988 "The Organization of Curve Detection: Coarse Tangent Fields and Fine Spline Coverings". Proceedings: Second International Conference on Computer Vision, IEEE Computer Society, Tampa FL 568-577.