Plato's Cave: Directed Diffusion
The Directed Diffusion Model
The Directed Diffusion model [Lehar 1994], which is an extension of
the
Boundary Contour System,
provides a computational implementation of this Gestalt concept in a
neural network architecture. In this model, oriented edge detectors
respond to the presence of oriented edges in the input by spatial
receptive fields in the manner of cortical simple cells reported by
Hubel and Wiesel. The response of such a cell computed as an image
convolution is proportional to the contrast across the edge. The
figure below illustrates two horizontal oriented cells responding to
two horizontal edges in the Kanizsa figure by way of oriented
receptive fields. Similar edge sensitive cells representing edges of
all orientations (not shown) are also present at every spatial
location in the system.
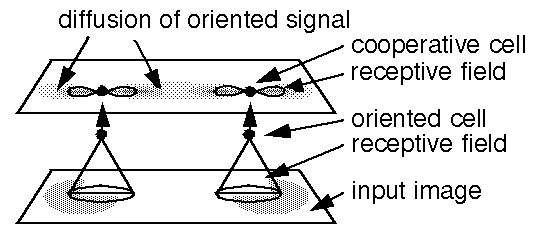
The spatial interactions responsible for illusory boundary
formation occur in a higher level cooperative cell layer, which also
contains cells representing all orientations at every spatial
location, and these cooperative cells receive input from the
corresponding oriented cells in the oriented layer. In the figure
above, for example the activation of the horizontal oriented cells
stimulates horizontal cooperative cells at those same
locations. Neural activation diffuses in the cooperative layer in an
orientation specific manner by way of bipolar receptive fields,
whereby cooperative cells receive input from other like-oriented cells
in the cooperative layer through the cooperative receptive fields. For
example in the figure, each horizontal cell in the cooperative layer
has a pair of horizontally oriented receptive fields which receive
input from other horizontal cooperative cells which are horizontally
adjacent to them.
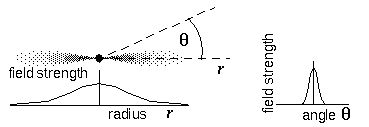
The figure below illustrates a possible form for the cooperative
receptive field, which can be defined by a Gaussian function of radial
distance from the cell, as well as a Gaussian function of angular
deviation from the line of colinearity. Cooperative cells which are
horizontally adjacent to the active cells depicted above will receive
input from the active cells. This secondary activation will continue
to propagate to other cooperative cells still further from the input
in a colinear direction. A passive decay term in the differential
equation governing the cooperative cell prevents runaway positive
feedback so that the pattern due to an isolated input will define at
equilibrium a spatially decaying trail of activation colinear with the
original edge, and extending outward to a distance which is a function
of the magnitude or contrast of the original edge. The equilibrium
pattern of diffusion from an isolated edge signal would therefore
appear similar in form to the Gaussian receptive field shown below
except that the final range of diffusion would be much greater than
the size of any individual receptive field, as suggested in the figure
above, and the range would be greater still at locations between
colinear oriented inducers where the cooperative cells would receive
activation from both sides simultaneously.
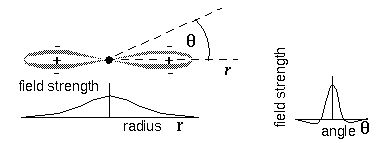
The subjective
appearance of the illusory contour in the Kanizsa figure however is not a broad diffuse region as
shown above, but looks more like a sharp well defined edge. In order to
achieve this result, an element of
spatial sharpening was incorporated in the Directed Diffusion model by
the addition of inhibitory
sidelobes to the cooperative receptive fields. This was achieved by
defining a difference of Gaussians profile as a function of angular
deviation as shown below,
rather than the straight
Gaussian profile shown above. This has the effect of boosting the
strength of the illusory contour along the crest of greatest magnitude, and suppressing it to
either side of that crest.
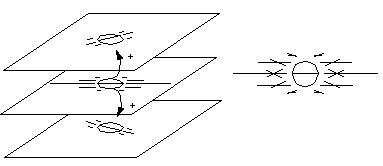
At every spatial location a certain cross-talk between adjacent
orientations was also defined in the model, resulting in an additional
diffusion of activation across orientations at each spatial location,
as suggested below (left). This orientational cross-talk results in a
fanning-out of the diffusing signal, as suggested below (right). This
feature allows boundary completion to occur around smooth curves, as
seen in the curved Kanizsa illusion, since the cooperative cells along
the curve receive activation from both sides simultaneously, and thus
become more active than cells along either line of colinearity. The
strength of the resulting illusory contour will however be somewhat
diminished, as is seen in the psychophysical studies.
Return to argument
Return to Steve Lehar




