Plato's Cave: Inverse Perspective Transformation
The Inverse Perspective Transformation
The laws of perspective transform the parallel rails of a railroad
track into converging lines that meet at the horizon. The job of the
visual system is to undo this transformation and to restore the
percept of parallel tracks, while giving the viewer information about
the angle from which those tracks are being viewed.
The architecture of the bubble world model has the property of
automatically performing this inverse perspective transformation.
Generally speaking, this is achieved by applying the same perspective
transformation to the infinite Euclidean grid or Cartesian coordinate
system, and then using this "bent ruler" as a measure of straightness
in the perspective-distorted world.
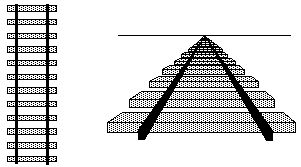
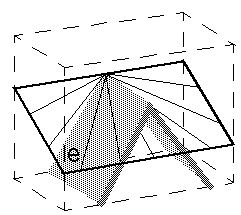
In particular, this is how it works. We begin by inverse-projecting
the image of the converging rails onto the front face of a slice of
the perceptual mechanism as described in the bubble model, which
produces an inverted "V" shaped "peaked roof" of influence through the
depth dimension as shown below. The difference in the bubble
world model is that the texture of neural connectivity, or
direction along which collinearity and coplanarity operations tend to
diffuse is no longer rectilinear, but follows a nonlinear pattern. In
particular, the back plane represents perceptual infinity. This block
of perceptual tissue therefore represents a rectangular slice from the
periphery of the perceptual sphere, viewed from the inside. In order
to describe the direction of this texture of connectivity within this
block, consider the set of planes a through
g below, which pass through a horizontal line at the
vertex of the inverted "V". Planes a and
g follow the back surface of the block, and thus
represent perceptual infinity, while plane d runs
horizontally, and passes through the "eye of the observer" at the
center of the perceptual sphere.
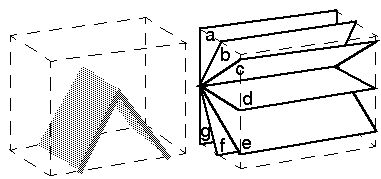
The figure below represents the texture of connectivity within each of
these planes, depicted as shown above, i.e. viewed from "below" for
planes a through c, and from "above"
for planes d through g. You can see
that the texture defines a set of converging lines, but the angle of
convergence varies from plane to plane.
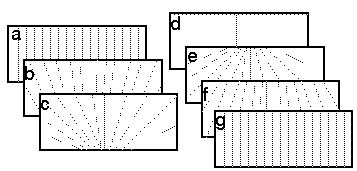
These converging lines represent the expected texture of convergence
of parallel edges on a surface viewed from various angles. For
example, plane e represents the perspective view of a
horizontal plane as seen from slightly above, like a tiled floor
viewed in perspective, whereas plane f represents
that same horizontal plane viewed from a higher vantage point. Planes
b and c represent the view of a
surface from below, like an overhead tiled ceiling. Planes
a and g represent the extreme case
of a tiled wall seen at infinity, i.e. like a birds-eye view with no
perspective distortion, while plane d represents the
singularity of a plane viewed from within the plane, i.e. everything
is collapsed into a single horizon line.
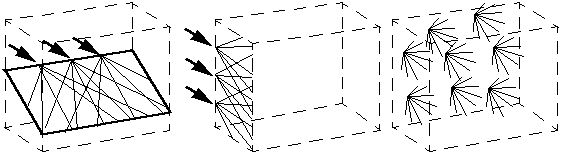
Now in fact this planar view of the connectivity in the perceptual
sphere is somewhat of a simplification, because horizontally within
each plane there are many such vanishing points, as suggested below
(left), and vertically there are many such sets of planes, as
suggested below (center), so the true situation is something like the
figure below (right), i.e. the external surface of the perceptual
sphere is a continuum of intersecting vanishing point vertices,
although it is to be remembered that this surface is actually
spherical, so the central axes of all of these vertices actually meet
at the center of the perceptual sphere. Each of these vertices
therefore represents the Cartesian grid rotated so that a major axis
passes through that point, and thus represents the perspective view of
that grid at that orientation as viewed from the origin.
Now that I have defined more precisely the connectivity architecture
of the perceptual sphere, it becomes clear how this architecture
automatically performs the inverse perspective transformation. For
when a pattern of converging lines is inverse-projected through this
structure, it will coincide with only one of these many sets
of converging lines. In our example, of all the multiple sets of
converging lines in the system, only those in plane e
match the angle of convergence of the rails in the image.
An interesting feature of this system is that besides simply
abstracting this geometrical information from a pair of
lines, the system then tends to reify the surface suggested
by those lines. In this case the stimulus of the converging lines in
plane e will tend to propagate coplanar activation
throughout plane e, thus filling-in every point in
the surface suggested by those lines. The filled-in surface will
automatically be represented at the correct distance and orientation
relative to the egocentric point, at the center of the perceptual
sphere. Any additional visual cues which are consistent with
the perceived surface would strengthen that percept and give it a more
precise perceived form and place, while any cues which were
inconsistent with it would tend to suppress the percept of
that surface.
This mechanism now offers an explanation for the Ponzo illusion, where
the two vertical lines appear to have different lengths, due to the
presence of the converging lines which suggest a depth interpretation.
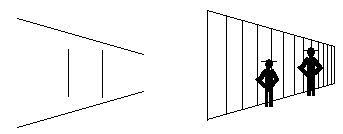
The Ponzo Illusion
This mechanism also explains the Mueller / Lyer illusion where the
vertical lines which are of the same length appear to be of different
lengths. Again this illusion makes sense in a spatial context,
because the line which is made to appear farther in depth becomes
perceptually larger, while the one that is made to appear closer in
depth becomes smaller.
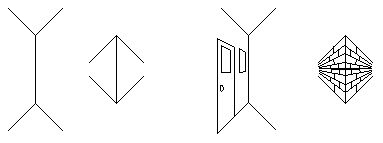
The Mueller / Lyer Illusion
Return to argument
Return to Steve Lehar







