Plato's Cave: Invariant Representation
Bottom-Up Invariant Recognition
An interesting relationship can be seen in the orientational harmonic
system in the relationship between the spatial pattern of orientations
produced by the standing waves in the system, and the corresponding
temporal frequencies that result from such standing waves.
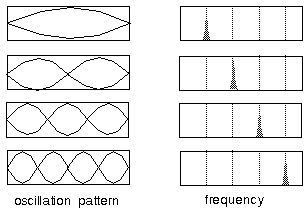
The temporal frequency of a standing wave is equal to the wavelength
divided by the speed of sound in the medium, which is a constant, so
that the temporal frequency is proportional to the wavelength. A
fourth harmonic standing wave for example will produce twice the
temporal frequency of a second harmonic which in turn is twice the
frequency of the first harmonic waveform. The significance of this
relationship is that the temporal frequency is a non-spatial quantity,
represented by a single value, while the corresponding standing wave
is a spatial pattern with a spatial, or orientational frequency, and a
phase, or absolute orientation. A single temporal frequency in the
orientational harmonic system therefore represents all the possible
orientations of the corresponding orientational frequency pattern in a
many-to-one manner.
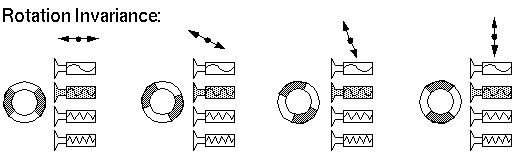
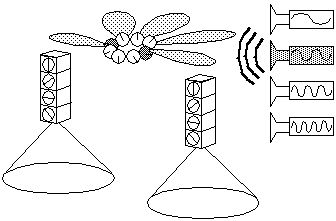
Consider a bank of tuned filters set to respond specifically to the
harmonics of a circular harmonic system. The second harmonic filter
for example would respond equally to a second harmonic pattern at any
orientation, as shown below. These tuned filters therefore represent
a rotation invariant representation of the pattern of standing waves
in the system.
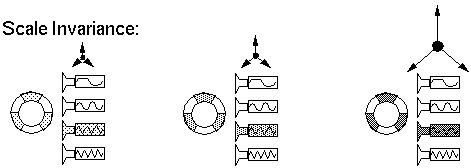
Since the patterns are themselves expressed in terms of angles, and
angles by their nature are invariant to scale, the orientational
representation is fundamentally invariant to changes in scale, so
again, the system has a natural scale invariance property.
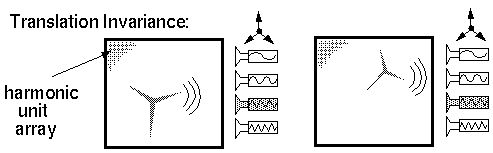
Finally, translation invariance can also be added to the system by
replicating the harmonic units in a spatial array, and arranging
global tuned filters which can receive input from all of the
units in the array simultaneously. The presence of a third harmonic
vertex anywhere in this array would therefore stimulate the
third harmonic filter in a rotation, translation, and scale invariant
manner.
Top-Down Specific Completion
An even more interesting feature of this system is seen by replacing
the bank of tuned filters by a bank of oscillators, which can be made
to broadcast a temporal frequency corresponding to any of the patterns
of standing waves. This will stimulate a standing wave in the
resonant system, i.e. the system can be made to "hallucinate" that
pattern as if it were detected in the input.
Because of the many-to-one invariance relationship between the
multiple rotations of a pattern and its single tuned oscillator, such
top-down priming does not specify the rotation of the resultant
pattern, but rather stimulates all rotations simultaneously. In the
presence of a weak or partial input on the other
hand, the emergent pattern will rotate to the orientation which best
matches both the bottom-up input and the top-down prime. This will
become clear in the following computer simulation.
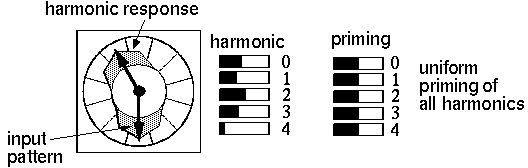
The figure below represents a single harmonic unit, and the black
arrows represent an input pattern composed in this case of two edges
in a near-collinear vertex. The gray shading represents the response
of the harmonic ring to this input, as calculated in the simulation.
The slider bars to the right of the ring represent the response of the
first few harmonics of the system to this input pattern. These
sliders thus correspond to the tuned filters. The pattern of these
sliders indicates a strong response to the second harmonic, and a
weaker response to the third harmonic. The sliders at the far right
represent the top-down priming signal corresponding to the tuned
oscillators for top-down priming. In the actual system the filters
and oscillators would be combined in a single unit, but are shown
separately here to separate the bottom-up from the top-down
signals. In this case all the top-down sliders are set at the same
value, indicating uniform priming of all harmonics.
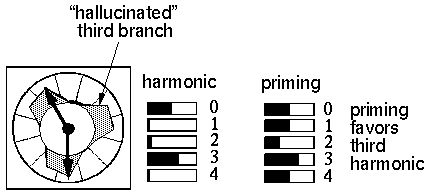
Given the same visual input, the system was then progressively primed
by reducing the second harmonic while boosting the third harmonic
prime. At first little change was observed in the system, but then at
a certain critical priming value, the system suddenly cascaded into
the state shown below, where the second harmonic response dropped
dramatically, while the third harmonic rose. At the same time a
change was seen in the harmonic ring as an illusory third branch was
"hallucinated" from the input pattern. What is interesting in this
simulation is that while the top-down prime was non-specific to
orientation, the result of this prime was very specific to
orientation, making a precise prediction of where a third branch
should be expected if this input were interpreted as a three-way,
rather than a two-way vertex.
This property of generalized recognition with many-to-one compression
from many instances to a single invariant code, combined with specific
completion with a one-to-many, or rather one-to-one-of-many
specification of the single variant which best matches both the
bottom-up input and the top-down prime, is a natural property of
harmonic resonance, and as far as I can tell, it is unique to harmonic
resonance. This concept will be elaborated further in the example
below.
Consider an array of harmonic units on which is projected a visual
input, represented by the black lines below, which produces a response
in the harmonic units, indicated by the gray regions. A bank of tuned
resonators behaving either as filters or as oscillators, are arranged
so as to receive input from, or broadcast output to the entire array
simultaneously.
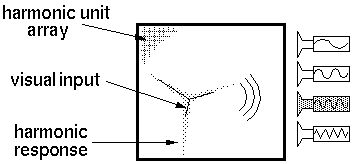
If a third harmonic pattern, i.e. a three-way vertex were presented to
this system, the harmonic units would produce a characteristic third
harmonic tone in temporal frequency, which would stimulate the third
harmonic resonator regardless of the location, the rotation, or the
scale of the pattern, as shown above. In other words the tone remains
constant through any rotations, translations, or scaling of the input
pattern. This represents a many-to-one transformation from an
infinite variety of instances to a single invariant feature which is
detected by the tuned filters.
In the top-down mode, the resonator can behave as a tuned oscillator
that transmits the third harmonic acoustic frequency and broadcasts it
to all the harmonic units in the array. Each unit in the array would
attempt to "hallucinate" a triangular vertex, but the overlapping and
intersecting signals would cancel each other out, resulting in an
approximately uniform pattern of activation, as suggested below.
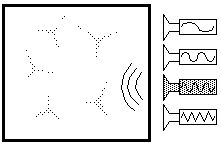
A visual input applied during such priming would break the symmetry of
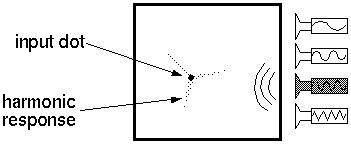
this mutual inhibition, and triangular stars would begin to
appear. Given an input in the form of a single dot, for example, this
input would favor triangular stars of all orientations equally at that
location, so that with sufficient top-down priming the system would
hallucinate the primed feature centered at the dot, at some arbitrary
orientation, as shown below. In this case only the location of the
primed pattern is constrained by the input, so that the other degrees
of freedom remain arbitrary.
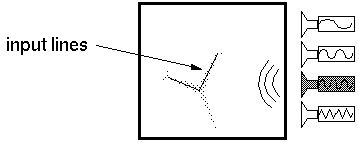
If the input supplied is more specific, then the resultant pattern
will be further constrained, as shown below, where the input consists
of two oriented edges that meet at a vertex. The minimum energy
configuration for this input is to have two arms of the third harmonic
response coincide with these lines, leaving the third to bisect the
external angle with an illusory boundary. This illusory filling-in or
completion of the expected form would respond to rotation, or
translation of the partial input so as to always perform completion in
the proper location and orientation.
Return to argument
Extension to a Hierarchical Representation
The invariance in recognition, and specificity in completion
demonstrated above occur through transformation across one level in a
hierarchy. The concept can be imagined to extend to multiple levels
in a hierarchical representation, preserving the invariance at each
level. If the orientational harmonic representation described above
represents geometrical form by way of symmetries (= orientational
periodicities) between visual edges, then the next higher level in the
visual hierarchy might encode symmetries of these symmetries. For
example a triangle might be encoded as a three-way arrangement of
vertices, whereas a square represents a four-way arrangement of
vertices about a center of symmetry. The next figure suggests how
such a system can be imagined to operate, to represent a square in a
rotation, translation, and scale invariant manner. The square is
defined by four right angled "L" vertices arranged in a
quadrilaterally symmetrical pattern. This central symmetry is
represented in the higher level by an array of orientational harmonic
units as described above, responding to a fourth harmonic tone,
resulting in a pattern of activation in the form of a four way vertex,
or cross.
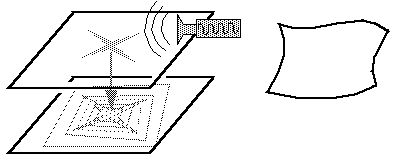
This pattern of activation propagates in turn down to a similar lower
level representation, but this time representing vertices
rather than edges. A four-way pattern of vertices suggests a square,
and would stimulate boundary and vertex completion at the lower level
between the four vertices to form a square, although the spatial scale
of the square would be undetermined. Competition between the
alternative squares at different scales would suppress the
alternatives as soon as one instance becomes dominant. Notice how the
central symmetry of the square can occur at any location and
orientation, and the pattern of orientations that it generates at the
lower level is compatible with squares at any scale. The appearance of
any instance of a right angled vertex in the input would anchor the
pattern at that vertex, fixing the approximate orientation of the
whole square, but allowing for a considerable amount of flex in the
exact location of other corners of the square. The pattern shown
above (right) for example is sufficiently similar to a square as to be
able to activate the generalized square node, because it has the same
central quadrilateral symmetry, which connects flexibly to four
vertices, that in turn connect to each other by way of flexible
boundaries. This model suggests that the lower-level details of the
corners, edges, and surfaces of shapes are not be encoded at the
higher level, but are left for the lower levels of the hierarchy to
complete. Each level of the hierarchy therefore encodes only the
information pertinent to the representation at that level, but unlike
other proposed schemes of visual abstraction, a top-down reification
allows for a transformation of any high level signal into a low-level
instantiation of that invariant form.
Return to argument
Implications
This model raises several interesting issues of relevance to visual
perception and representation. In many visual models, features are
extracted from the input by specialized feature detectors, the
response to each feature being represented by the activation of the
corresponding node. In models that involve competition or cooperation
between features, that interaction is often implemented by lateral
inhibition or excitation between these higher level nodes. The system
proposed here is fundamentally different in the sense that what
competition or cooperation exists in the model, occurs not by
way of explicit interactions between high level representations, but
rather occurs node by node at the lower level of
representation by way of constructive and destructive interference
between competing waveforms in a distributed representation. Indeed,
that interaction between competing representations occurs independent
of the higher level representation, and can be seen as a low level
consistency matching at the highest possible resolution in
the system between alternative interpretations of the input signal.
The manner in which the top-down priming influences perception in the
system is also noteworthy. In the computer simulation presented above,
the ambiguous input pattern stimulated both the second and the third
orientational harmonics, leading to an activation of the second and
third harmonic filters. In a purely feedforward system, this higher
level abstraction of the lower level pattern would be the only
information available to a recognition or decision process. But the
dimensionality of this abstraction, one value for each encoded
pattern, is far more impoverished or compressed than the intricate
balance of competing waveforms in the lower level cooperative
representation. Indeed the interactions between the multiple waveforms
present in that representation is not reducible to a single dimension
without a great loss of resolution. During the dynamic simulation,
when the top-down bias favoring the third harmonic is first applied,
the interactions between waveforms in the cooperative representation
was observed to slowly bend the activations of the two branches of the
bilateral pattern against their natural tendency to remain colinear,
in an attempt to make room for a third branch, even though the
bottom-up second harmonic signal still dominated the third harmonic
signal. A sudden change was seen to occur as soon as an illusory third
branch sprouts, after which the system quickly re-equilibrates to a
third harmonic condition as the third branch grows in size and the
bottom-up feature representation reflects a predominantly third
harmonic pattern. In this system therefore, the priming of the third
harmonic resonator initiates a fundamental shift in the balance of
forces at the lower level cooperative representation, causing the
pattern there to bend as if under stress, as the third harmonic
attempts to establish a third branch of activation.
The success of this priming on changing the final percept depends
intimately on the context at the lower level, whether the rest of the
inputs at that location, and at neighboring locations in a full
simulation, are also consistent with this new trilateral pattern. In
a full simulation complete with neighboring units and oriented input,
the bending of the two arms of the bilateral pattern would subtly
shift the forces in all the neighboring cooperative units, resulting
in a different dynamic balance of forces throughout the cooperative
layer. This new balance of forces could either promote the growth of
the third branch (by increasing the activation at the two and three
o'clock orientations), or inhibit it, in a way that would be
impossible to predict by analysis of the high level representation
alone. The manner of operation of the top down priming in this system
therefore is not in the form of an "intellectual" competition between
the high level abstractions represented by the second and third
harmonic resonators, but rather, the competition is more of a
"physical" struggle between the low level embodiments of these high
level nodes, in the context of the lattice of interacting
forces in the cooperative layer. The top level nodes communicate the
urgency, and monitor the outcome of the competition between
representations, but the competition itself takes place at the lowest
level between the waveforms themselves. In this system therefore, the
top down priming is a highly context sensitive operation.
Return to argument
Return to Steve Lehar












