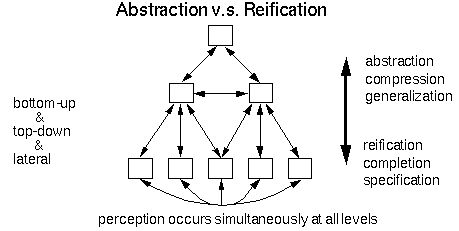
I have adopted the word reification to indicate the inverse operation to abstraction. Abstraction implies a many-to-one transformation from the many possible variants to a single invariant form. Reification on the other hand implies not a one-to-many transformation, which would potentially produce an infinite variety of variants, but rather a one-to-one-of-many transformation, although the exact variant that is generated could be any one of the infinite variety of variant forms.
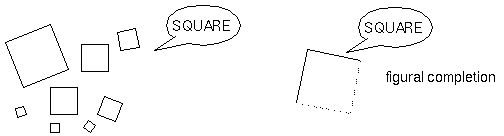
For example, imagine a "node" (cell? cell assembly? pattern of activation?) in your brain which represents the concept "square", and which "lights up" in the presence of any square at any rotation, translation, or scale. A "top-down" activation of that node would potentially be able to generate a low-level representation of any one of those squares. In the absence of a visual input, such a reification would produce any one of those possible squares. In the presence of a partial input on the other hand, the reification would produce the single square which most closely matches both the bottom-up partial input, and the top-down invariant square. The reification would therefore produce a figural completion, or filling-in of missing information which is specific to the partial input provided.