A novel approach to modeling spatial perception is presented based on the Gestalt principles of isomorphism and emergence. The principle of isomorphism suggests that the subjective experience of perception is a valid source of evidence for the information that must be encoded neurophysiologically. This in turn validates the concept of perceptual modeling, that is modeling the percept as observed rather than the neural mechanism by which it is subserved. Evidence for emergence suggests that global perceptual states develop dynamically under the parallel action of a multitude of local forces. Taken together these principles suggest that the perception of space emerges dynamically as a single global decision via a multitude of local interactions within a spatial medium. This paper offers a preliminary sketch of one kind of dynamic computational mechanism capable of exhibiting these Gestalt properties. Perhaps the greatest promise of this approach is that it can account for many complex aspects of perception, such as the perception of transparency, mutual illumination between objects, multiple light sources, attached and cast shadows, using computational principles developed to address the perception of simple geometrical forms under a single source of illumination.
Neurophysiological studies have on the whole emphasized the specialization of different visual areas for the processing of perceptual attributes, such as color, motion, and stereopsis. Psychophysical studies on the other hand, however generally reveal integration rather than segregation in perception (Nakayama et al. 1990). Indeed the subjective experience of perception is of a single unified whole rather than a mosaic of separate perceptual components. The primary focus of this paper is to address the issue of integration in perception, with reference to the Gestalt principles of isomorphism and emergence. Lehar & McLoughlin (1998) suggested that the principle of isomorphism can be used to validate a perceptual modeling approach, i.e. to model the information manifest in the subjective experience of perception, as opposed to the neural mechanism by which perception is subserved. Perceptual modeling in turn reveals a general principle of reification in perception, i.e. a filling-in of a more complete and explicit perceptual representation based on the more impoverished sensory stimulus. Lehar & McLoughlin (1998) also discuss the Gestalt principle of emergence, i.e. the way that global perceptual entities emerge under the parallel action of a multitude of local forces. These concepts were illustrated by a model of brightness perception composed of distinct representational levels that were dynamically coupled in such a way that a feature present at one level of the representation has an immediate and profound influence on other levels of the representation.
In the present paper the principle of isomorphism is extended to account for the nature of spatial perception, and to model the intimate coupling observed between the perception of surface brightness, surface reflectance, and perceived direction of illumination, with the perception of three-dimensional form. It will also be shown that this approach offers a solution to many troublesome issues in visual perception, such as the perception of transparency, complex or fragmented surfaces, attached and cast shadows, specular reflection, multiple light sources, mutual illumination between objects, and diffuse illumination, all by way of a single general computational strategy.
The neural representation of space is an enigma. While one's subjective experience is of a fully spatial world, the retinal image on which this is based is fundamentally two-dimensional. This has led to numerous proposals as to the type of neural representation necessary to account for spatial perception. The Gestalt principle of isomorphism offers us one way to circumvent this thorny issue by modeling the percept as observed subjectively, rather than its neural representation. This is of course only an interim solution, as the neurophysiological mechanism must eventually also be identified. It is proposed that identifying the information encoded in perception will help to identify the underlying neurophysiological mechanisms.
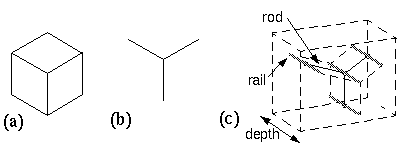
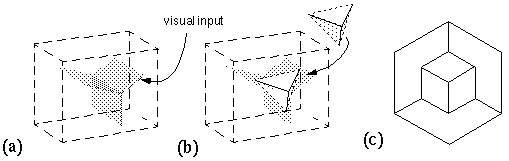
Consider the visual stimulus depicted in figure 1 a. The spatial percept that results from this two-dimensional combination of edges is that of a solid three-dimensional object. This produces an explicit depth value at every point on every visible surface, as well as the amodal percept of the object completing behind the three visible surfaces. This percept represents a clear case of reification, i.e. the subjective percept contains more explicit spatial information than that present in the visual stimulus. Since depth is not explicitly encoded in the input image, the problem addressed by perception is to determine what combination of possible surfaces in depth correspond to the most likely configuration of the depicted solid. This is the inverse optics problem, which is underconstrained, as there are an infinite number of possible three-dimensional configurations that correspond to any two-dimensional projection. Arnheim (1969a) presents an insightful analysis of this problem, which can be reformulated as follows. Consider (for simplicity) just the central "Y" vertex in figure 1 a, depicted in figure 1 b. Arnheim proposes that the perceptual constraints of inverse optics can be expressed using a rod-and-rail analogy as shown in figure 1 c. The three rods, representing the three edges in the visual input, are constrained in two dimensions to the configuration seen in the input, but are free to slide in depth along four rails as depicted in figure 1 c. The rods must be infinitely elastic between their end-points, so that they can expand and contract in length. The rods can therefore take on any of the infinite three-dimensional configurations corresponding to the two-dimensional input of figure 1 b. While this problem is theoretically underconstrained, the final percept tends to represent the configuration that offers the greatest simplicity, or prägnanz, as measured in a three-dimensional context (Hochberg et al. 1960). In the case of figure 1 a its simplest interpretation corresponds to a cube with equal sides and right angles throughout.

(a) A line drawing that stimulates a volumetric spatial percept with an explicit depth value at every point on every visible surface, and an amodal percept of the hidden rear surfaces. (b) The central "Y" vertex from (a), which tends to be perceived as a corner in depth. (c) A dynamic rod-and-rail model of the emergence of the depth percept in (b) by relaxation of local constraints in depth.
A number of computational approaches to this problem have been proposed (Barrow et al. 1981, Ullman 1984, Fischler et al. 1992, Sinha et al. 1993, Adelson et al. 1996). They all minimize some measure of three-dimensional simplicity by allowing the spatial percept to deform in depth until a minimum is achieved. Configurational constraints, for example the fact that corners tend to be perceived as right angles can be incorporated into such a scheme. This kind of algorithm is therefore consistent with the Gestalt principle of isomorphism, since it reifies a three-dimensional data structure from a two-dimensional input, and defines a multi-stable dynamic system whose stable states represent the final percept.
In all of the preceding models, there is a sequential progression of abstraction, explicit or implied, through the different stages of the algorithm. The first stage involves the detection of edges in the input to produce a more abstracted representation of the scene. Subsequent relaxation processing depends critically on the assumption that this initial stage was successful, and that all detected edges are valid, as the analytical algorithms for extracting three-dimensional form are particularly vulnerable to noise or error in the data on which they operate. As a consequence these approaches are not typically applied to natural scenes which contain complicated lighting conditions and complex or fragmented surfaces. While some of these models exhibit multistability in their final stage, this multistability does not extend down to the levels of edge and surface detection. Yet we know from visual illusions, such as the Kanizsa figure and the Ehrenstein illusion, that the global spatial interpretation has a profound effect on the percerption of local edges. The objective of the present modeling approach is to demonstrate how the principles of emergence and multistability can be extended throughout the visual hierarchy, such that while the perception of local elements leads to a global perceived form, the global structure influences how the component edges and surfaces are perceived. This coupling between local and global emergence ensures that the coupled system only acknowledges edges that are consistent with the globally perceived configuration, and conversely, only recognizes global configurations that are consistent with the edges it identifies as significant form cues.
The model developed herein is presented as a general account of the organizational principles of vision, rather than as a detailed instantiation of any specific computational approach. While this account is somewhat vague in parts, the concepts behind this approach are clearly specified:
Spatial perception involves spatial computation in a spatial medium.
The percept is reified to greater detail than the sensory input on which it is based.
Field-like interactions dynamically couple large regions of the percept in a spatially coherent manner.
Interactions between different perceptual modules occurs in a low-level point-for-point manner.
The final perceptual state emerges as a single global decision under the influence of multiple local forces.
These general principles are advanced herein, and a model is described chiefly to clarify the meaning of these concepts. This model therefore represents more of a commentary on the assumptions underlying the current direction of vision research, than a complete model of the mechanisms of vision.
The Gestalt bubble analogy as elaborated by Attneave (1982) provides the inspiration for the following model of spatial perception. The dynamics of a bubble surface suggest a mechanism that performs a three-dimensional interpolation of smoothness from information at the boundaries. This kind of surface interpolation can most easily be calculated in a fully spatial context, as suggested by Barrow et al. (1981). The modeling begins therefore with a three-dimensional matrix of dynamic computational elements in a block, or volume representing perceived space (figure 2 a) Each element in this block can be in one of two states, transparent (figure 2 b) or opaque, the latter representing the perception of an opaque surface at a particular location and depth. Elements in the opaque state also take on a surface orientation value in three dimensions, and interact with adjacent elements in a coplanar manner. This coplanarity constraint can be expressed as a local field-like interaction between adjacent opaque-state elements in a direction coplanar with their orientation (figure 2 c). In other words, a local element in the opaque state tends to recruit adjacent elements in the same plane and orientation. Thus a surface defined by opaque-state units tends to propagate spatially, in a manner analogous to the diffusion of a brightness signal (Lehar & McLoughlin, 1998,) except that this diffusion occurs explicitly in depth, like the surface of a soap bubble. Unlike the soap bubble analogy, the percept is not a physical surface but merely a plane of active elements within a volumetric matrix. The appendix provides one example of a more detailed mathematical description of this local coplanarity field of opaque state units.
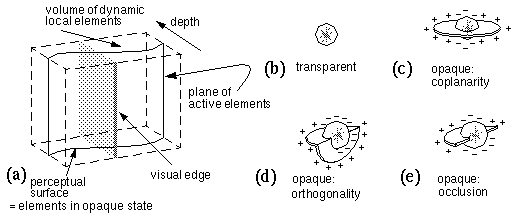
(a) The Gestalt Bubble model consisting of a block of dynamic local elements which can be in one of several states. (b) The transparent state, no neighborhood interactions. (c) The opaque coplanarity state which tends to complete smooth surfaces. (d) The opaque orthogonality state which tends to complete perceptual corners. (e) The opaque occlusion state which tends to complete surface edges.
A visual edge has the effect of producing a corner or crease in the perceived surface, as seen in figure 1 a and b. Within our model, a two-dimensional visual edge is projected onto the front face of the perceptual block, and propagates its influence in depth throughout the volume of the block, as suggested by the light shading in figure 2 a. This changes the opaque-state elements within its field of influence from a coplanar interaction to an orthogonal, or corner interaction as suggested by the local force field in figure 2 d. The corner of this field should align parallel to the visual edge in two dimensions, but otherwise remain unconstrained in orientation except by local interaction with adjacent opaque units. Visual edges can also denote occlusion, and so opaque-state elements can also exist in an occlusion state, with a coplanarity interaction in one direction only, as suggested by the occlusion field in figure 2 e. Hence, in the presence of a single visual edge, a local element in the opaque state should have an equal probability of changing into the orthogonality or occlusion state, with the orthogonal or occlusion edge aligned parallel to the inducing visual edge. Elements in the orthogonal state tend to promote orthogonality in adjacent elements along the perceived corner, while elements in the occlusion state promote occlusion along that edge. In other words, an edge will tend to be perceived as a corner or occlusion percept along its entire length, although the whole edge may change state back and forth as a unit in a multistable manner. The appendix presents a more detailed mathematical description of how these orthogonality and occlusion fields might be defined. The presence of the visual edge in figure 2 a therefore tends to crease or break the perceived surface into one of the different possible configurations shown in figure 3 a through d. The final configuration selected by the system would depend not only on the local image region depicted in figure 3, but also on forces from adjacent regions of the image.
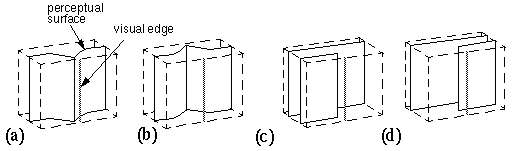
(a) through (d): Several possible stable states of the Gestalt bubble model in response to a single visual edge.
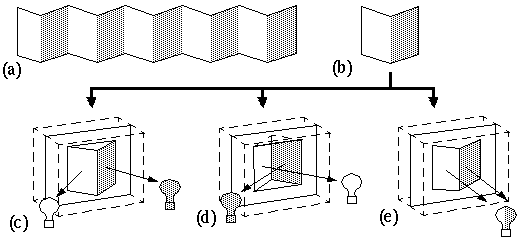
The global properties of the model presented below are advanced not as inevitable consequences of the local field-like forces described in the appendix, but rather as the global properties that must be achieved to account for the corresponding global effects observed in perception. Collinear boundary completion is expressed within this model as a physical process analogous to the propagation of a crack or fold in a physical medium. A visual edge which fades gradually produces a crease in the perceptual medium that tends to propagate outward beyond the visual edge (figure 4 a). If two such edges are found in a collinear configuration, the perceptual surface will tend to crease or fold between them (figure 4 b). This tendency is accentuated if additional evidence from adjacent regions support this configuration. This can be seen in figure 4 d where fading horizontal lines can link up across the figure to change the percept from a regular hexagon (figure 4 c) into a folded rectangle in depth (figure 4 d).
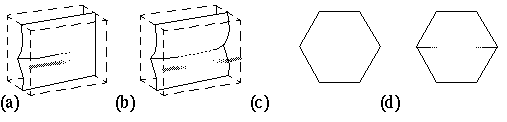
(a) Boundary completion in the bubble model: A single line ending creates a crease in the perceptual surface. (b) Two line endings generate a crease joining them. (c) A regular hexagon figure transforms into (d) a percept of a folded surface with the addition of suggestive lines, with the assistance of a global gestalt that supports the perception of a folded surface in depth.
The Gestalt theorists recognized that closure was a significant factor in perceptual segmentation, since an enclosed contour is seen to promote a figure / ground segregation (Koffka 1935 p. 178). For example an outline square (figure 5 a) tends to be seen as a square surface in front of a background surface that is complete and continuous behind the square. The problem is that closure is a `gestaltqualität', a quality defined by a global configuration that is difficult to specify in terms of any local featural requirements, especially in the case of irregular or fragmented contours (figure 5 b). Within this model an enclosed contour breaks away a piece of the perceptual surface, completing the background amodally behind the occluding foreground figure (figure 5 c). In the presence of irregular or fragmented edges the influence of the individual edge fragments act collectively to break the perceptual surface along that contour (figure 5 d). The final scission of figure from ground is therefore driven not so much by the exact path of the individual irregular edges, as it is by the global configuration of the emergent gestalt.

(a) An enclosed contour produces a percept of an occluding foreground figure in front of a continuous background surface. (b) Even irregular and fragmented surfaces produce a figure / ground segregation. (c) The perception of closure and figure / ground segregation are explained in the bubble model exactly as perceived. (d) The perceived boundary of the fragmented figure follows the global emergent gestalt rather than any individual edge.
In the case of vertices or intersections between visual edges, the different edges interact with one another favoring a percept of a single vertex at that point. For example the three edges defining the three-way "Y" vertex shown in figure 1 b promote a percept of a single three-dimensional corner, whose depth depends on whether the corner is perceived as convex or concave. In the case of figure 1 a, the cubical percept constrains the central "Y" vertex as a convex rather than a concave trihedral percept. The thesis of the present model is that this dynamic behavior can conceivably be implemented using the same kinds of local field-forces described in the appendix to promote mutually orthogonal completion in three dimensions, wherever visual edges meet at an angle in two dimensions. figure 6 a depicts the three-dimensional influence of the two-dimensional Y-vertex when projected on the front face of the volumetric matrix. Each plane of this three-planed structure promotes the emergence of a corner or occlusion percept at some depth within that plane, however the three emergent edges interact with one another to favor the percept of a single vertex in depth, and a coplanar surface completion would tend to connect those corners to produce a trihedral surface percept, as suggested in figure 6 b. Any dimension of this percept that is not explicitly specified or constrained by the visual input, remains unconstrained. In other words, the trihedral percept is embedded in the volumetric matrix in such a way that its three component corner percepts are free to slide inward or outward in depth, to rotate through a small range of angles, to flip in bistable manner between a convex and concave trihedral configuration, and flip to an occlusion percept. This model now expresses the multistability of the rod-and-rail analogy shown in figure 1 c, but in a more generalized form that is no longer hard-wired to the Y-vertex input shown in figure 1 b, but can accomodate any arbitrary configuration of lines in the input image. A local visual feature like an isolated Y-vertex generally exhibits a larger number of stable states, whereas in the context of adjacent features the number of stable solutions is often diminished. This explains why the cubical percept of figure 1 a is stable, while its central Y-vertex alone as shown in figure 1 b is bistable. The fundamental multistability of figure 1 a is revealed by the addition of a different spatial context, as depicted in figure 6 c.
(a) The three-dimensional field of influence due to a two-dimensional Y-vertex projected into the depth dimension of the volumetric matrix. (b) One of many possible emergent surface percepts in responst to that stimulus, in the form of a convex trihedral surface percept. (c) The fundamental multistibility of figure 1 a revealed by the addition of a different spatial context.
Perspective cues offer another example of a computation that is inordinately complicated in most models, but in the fully reified spatial model perspective can be computed quite easily with only a small change in the geometry of our volumetric model. Figure 7 a, shows a trapezoid stimulus, which has a tendency to be perceived in depth, i.e. the shorter top side tends to be perceived as being the same length as the longer base, but apparently diminished by perspective. Arnheim (1969a) suggests a simple distortion to the volumetric model to account for this phenomenon, which can be reformulated as follows. The height and width of the volumetric matrix are diminished as a function of depth, as suggested in figure 7 b, transforming the block shape into a truncated pyramid that tapers in depth. The vertical and horizontal dimensions represented by that space however are not diminished, in other words, the larger front face and the smaller rear face of the volumetric structure represent equal areas in perceived space, by unequal areas in representational space, as suggested by the converging grid lines in the figure. All of the spatial interactions described above, for example the collinear propagation of corner and occlusion percepts, would be similarly distorted in this space. Even the angular measure of orthogonality is distorted somewhat by this transformation. For example the perceived cube depicted in the solid volume of figure 7 b is metrically shrunken in height and width as a function of depth, but since this shrinking is in the same proportion as the shrinking of the space itself, therefore the depicted irregular cube represents a percept of a regular cube with equal sides and orthogonal faces. The propagation of the field of influence in depth due to a two-dimensional visual input on the other hand does not shrink with depth. For example a projection of the trapezoid of figure 7 a would occur in this model as depicted in figure 7 c, projecting the trapezoidal form backward in parallel, independent of the convergence of the space around it. The shaded surfaces in figure 7 c therefore represent the locus of all possible spatial interpretations of the two-dimensional trapezoid stimulus of figure 7 a. For example one possible perceptual interpretation is of a trapezoid in the plane of the page, which can be perceived to be either nearer or farther in depth, but since the size scale shrinks as a function of depth, the percept will be experienced as larger in absolute size (as measured against the shrunken spatial scale) when perceived as farther away, and as smaller in absolute size (as measured against the expanded scale) when perceived to be closer in depth. This corresponds to the phenomenon known as Emmert's Law (Coren et al., 1994), whereby a retinal after-image appears larger when viewed against a distant background than when viewed against a nearer background. Now there are also an infinite number of alternative perceptual interpretations of the trapezoidal stimulus, some of which are depicted in dark shaded lines in figure 7 d. Most of these alternative percepts are geometrically irregular, representing figures with unequal sides and odd angles. But of all these possibilities, there is one special case, depicted in black lines in figure 7 d, in which the convergence of the sides of the perceived form happens to coincide exactly with the convergence of the space itself. In other words, this particular percept represents a regular rectangle viewed in perspective, with parallel sides and right angled corners. While this rectangular percept represents the most stable interpretation, other possible interpretations might be suggested by different contexts.
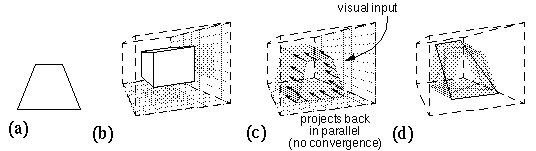
(a) A trapezoidal stimulus that tends to be perceived as a rectangle viewed in perspective. (b) The perspective modified spatial representation whose dimensions are shrunken in height and breadth as a function of depth. (c) The parallel projection of a field of influence into depth of the two-dimensional trapezoidal stimulus. (d) Several possible perceptual interpretations of the trapezoidal stimulus, one of which (depicted in black) represents a regular rectangle viewed in perspective.
The ideas presented so far make use of an explicit volumetric or "voxel" (volume pixel) representation of space. But Euclidean space is boundless, while the human skull is not. How can a boundless space be explicitly represented by a bounded substrate? The depth dimension can be represented by a vergence measure, which maps the infinity of Euclidean distance into a finite bounded range (figure 8 a). This produces a representation reminiscent of museum dioramas (figure 8 b), where objects in the foreground are represented in full depth, but the depth dimension gets increasingly compressed with distance from the viewer, eventually collapsing into a flat plane corresponding to the background. This vergence measure is presented here merely as a nonlinear compression of depth in a monocular spatial representation, as opposed to a real vergence value measured in a binocular system, although of course it could serve both purposes in biological vision. Assuming unit separation between the eyes in a binocular system, this compression is defined by the equation
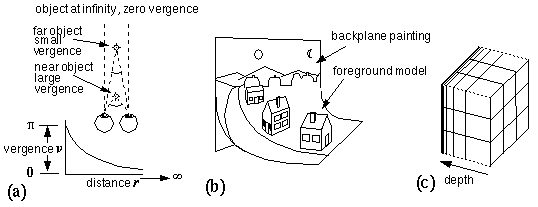
(a) A vergence representation maps infinite distance into a finite range. (b) This produces a mapping reminiscent of a museum diarama. (c) The compressed reference grid in this compressed space defines intervals that are perceived to be of uniform size.
where v is the vergence measure of depth, and r is the Euclidean range, or distance in depth. What does this kind of compression mean in an isomorphic representation? If the perceptual frame of reference is compressed along with the objects in that space, then the compression need not be perceptually apparent. Figure 8 c depicts one such compressed reference grid in our compressed space. Unequal intervals between adjacent grid lines in depth define intervals that are perceived to be of equal length, so the flattened cubes defined by the distorted grid would appear perceptually as regular cubes, of equal height, breadth, and depth. This compression of the reference grid to match the compression of the space would, in a mathematical system with infinite resolution, completely conceal the compression from the percipient. In a real physical implementation there are two effects of this compression that would remain apparent perceptually, due to the fact that the spatial matrix itself would have to have a finite perceptual resolution. The resolution of depth within this space is reduced as a function of depth, and beyond a certain limiting depth, all objects are perceived to be flattened into two dimensions, with zero extent in depth. This phenomenon is observed perceptually, where the sun, moon, and distant mountains appear perceptually as if they are pasted against the flat dome of the sky.
The other two dimensions of space can also be bounded by converting the x and y of Euclidean space into azimuth and elevation angles, a and b, producing an angle / angle / vergence representation (figure 9 a). Mathematically this transformation converts the point P(a,b,r) in polar coordinates to point Q(a,b,v) in this bounded spherical representation. In other words, azimuth and elevation angles are preserved by this transformation while the radial distance in depth r is compressed to the vergence representation v as described above. This spherical coordinate system has the ecological advantage that the space near the body is represented at the highest spatial resolution, whereas the less important more distant parts of space are represented at lower resolution. All depths beyond a certain radial distance are mapped to the surface of the representation which corresponds to perceptual infinity. Pinker (1988) derrives a very similar volumetric representation to account for the observed properties of mental imagery representation and manipulation.

(a) An azimuth / elevation / vergence representation maps the infinity of three-dimensional Euclidean space into a finite spherical space. (b) The infinite Cartesian grid (section) showing lines of collinearity at every angle through every point. (c) The deformation of the Cartesian grid caused by the perspective transformation of the azimuth / elevation / vergence representation. (d) A view of a man walking down a road represented in the perspective distorted space. (e) The shading indicates portions of the perceptual field that are outside the visual field; amodal features in this region are calculated by extrapolation from the visible portion. (f) A section of the spherical space depicted in the same format as the perspective space shown in figure 7 (b) and (c).
The transformation from the infinite Cartesian grid of figure 9 b to the angle / angle / vergence representation depicted in figure 9 c actually represents a perspective transformation on the Cartesian grid. In other words, the transformed space looks like a perspective view of a Cartesian grid when viewed from inside, with all parallel lines converging to a point in both directions. The significance of this observation is that by mapping space into a perspective-distorted grid, the distortion of perspective is removed, in the same way that plotting log data on a log plot removes the logarithmic component of the data. Consider a perspective view of the world cartooned in figure 9 d. If the distorted reference grid of figure 9 c is used to measure lines and distances in figure 9 d, the bowed line of the road on which the man is walking is aligned with the bowed reference grid, and therefore is perceived to be straight. However in a global sense there are peculiar distortions that are apparent to the percipient caused by this extreme deformation of Euclidean space. For while the sides of the road are perceived to be parallel, they are also perceived to meet at a point on the horizon. This paradox is so familiar in everyday experience as to seem totally unremarkable and yet it offers one of the strongest pieces of evidence for the curvature embodied in the present model. The fact that two lines can be perceived to be both straight and parallel and yet to converge to a point both in front and behind the percipient indicates that our internal representation itself must be curved. The proposed representation of space has exactly this property, that parallel lines do not extend to infinity but meet at a point beyond which they are no longer represented. Likewise the vertical walls of the houses in figure 9 d bow outwards away from the observer, but in doing so they follow the curvature of the reference lines in the grid of figure 9 c, and are therefore perceived as being both straight, and vertical. Since curved lines in this spherical representation represent straight lines in external space, all of the spatial interactions discussed in the previous section, including the coplanar interactions, and collinear creasing of perceived surfaces, must follow the grain or curvature of collinearity defined in this distorted coordinate system. The distance scale encoded in the grid of figure 9 c replaces the regularly spaced Cartesian grid by a nonlinear collapsing grid whose intervals are spaced ever closer as they approach perceptual infinity, but nevertheless, represent equal intervals in external space. This nonlinear collapsing scale thereby provides an objective measure of distance in the perspective-distorted perceptual world. For example the houses in figure 9 d would be perceived to be approximately the same size and depth, although the farther house is experienced at a lower perceptual resolution. Again, this accounts for another paradoxical but familiar property of perceived space whereby more distant objects are perceived to be both smaller, and yet at the same time to be perceived as undiminished in size. This corresponds to the difference in subject's reports depending on whether they are given objective v.s. projective instruction (Coren et al., 1994. p. 500) in how to report their observations, showing that both types of information are available perceptually. An interesting property of this representation is that different points on the bounding surface of the spherical representation represent different directions in space. All parallel lines which point in a particular direction converge to the same surface point representing that direction.
Figure 9 f depicts a slice of fixed height and width extending to perceptual infinity in one direction, cut from the spherical representation of figure 9 c. This slice is similar to the truncated pyramid shape shown in figure 7 b, with the difference that the horizontal and vertical scale of representational space diminishes in a nonlinear fashion as a function of distance in depth. In other words, the sides of the pyramid in figure 9 f converge in curves rather than in straight lines, and the pyramid is no longer truncated, but extends in depth all the way to the vanishing point at representational infinity. An input image is projected into this spherical space using the same principles as before; i.e. the image is copied onto the curved front face of the space shown in figure 9 f, or onto a spherical surface in front of the eyeball of the perceptual effigy in figure 9 e, from whence the image is projected radially outwards into the depth dimension along the radii of the spherical structure, as suggested by the arrows in in figure 9 e, to generate a three-dimensional percept of the world surrounding the observer. In a binocular system the images from the two eyes are projected outward in parallel, where their intersection within the spatial representation defines perceived depth by binocular disparity, exactly as proposed in the Projection Field Theory of binocular vision (Kaufman 1974, Boring 1933, Charnwood 1951, Marr et al. 1976, Julesz 1971).
The Gestalt Bubble model has another unusual property not normally encountered in models of vision. In most models the processing of the visual input is confined to the area of the input itself, just as in image processing. In this model however the purpose of visual processing is defined as a reification or completion of a percept of the complete local environment surrounding the observer, filling-in features that are outside of the visual field by extrapolation in exactly the same way that amodal completion interpolates edges that pass behind an occluder. In other words, the head is treated as an occluder of the world behind the head, and the final percept is of a spherical world surrounding the body, only part of which corresponds to the visual field. This is shown in figure 9 e, where the shaded portion represents the occluded visual world behind the head, and the faded lines in that region represent spatial edges and surfaces extrapolated from the visible portion of the representation.
This raises the question whether the world behind the head is actually perceived visually at all. Although the world behind the head is clearly not seen with the same vivid sensation of color and form as the world within the visual field, there is nevertheless a percept of space behind the body, as can be demonstrated by the fact that it is possible to take a step or two backwards without stumbling. A step (whether forwards or backwards) requires an accurate knowledge of the height and orientation of the ground at the point of contact. This becomes evident whenever a step encounters an unexpected change in surface height or orientation, even of as little as an inch or two, which inevitably results in a stumble. A backwards step without a stumble therefore indicates that the stepper has knowledge of these parameters within about an inch or two. Whether such information must necessarily be considered visual information is irrelevant at this point, since this model is advanced as a perceptual model in which visual, auditory, somatosensory, and other information are unified in a single coupled system, which is why a representation of the body percept is included at the center of the structure, whose postural configuration would be updated both visually, and from somatosensory and kinesthetic information. The model suggests that surfaces in the scene are extrapolated from their visible portions in the visual field into the unseen portion of the perceptual field. For example the walls and ceilings of a hallway would be completed perceptually behind the observer, as would such regular features as a handrail. This would explain how it is possible to accurately grab a handrail, pole, or surface at a point well outside of the visual field while viewing only the visible portion of the object. Like the backwards step, this performance clearly demonstrates the availability of high resolution spatial information about objects outside of the visual field. Both Gibson (Reed 1988) and the Gestaltists (Kanizsa 1979, Tampieri 1956, Attneave 1977, Arnheim 1969b p. 86) fully appreciated the significance of this aspect of amodal perception.
Our structural representation of three-dimensional space allows for low-level spatial computations of brightness, lightness, and illuminance. Figure 10 a depicts a simple bistable percept in which each pair of dark and light panels can be seen as either a convex or concave corner. (The spontaneous reversal of this kind of figure can be controlled somewhat by fixating on one vertex, which will then tend to be seen as convex) When a single pair of panels is isolated (figure 10 b) the percept becomes tri-stable, i.e. it can be seen as either a convex corner (figure 10 c), or a concave corner (figure 10 d), or as a pair of diamond shaped tiles in the plane of the page (figure 10 e). In an isomorphic model this change between the three stable states would be accompanied by a corresponding change in the state of the internal spatial representation. What is interesting in this percept is how the perception of the spatial structure is seen to influence the perception of the illuminant of the scene. When viewed as a convex corner the illuminant is perceived to the left, whereas when viewed as a concave corner the illuminant is perceived to the right. When seen as two diamond shaped tiles the illuminant becomes irrelevant, because the difference in brightness between the two tiles is now seen as a difference in reflectance rather than a difference in illumination. This example reveals the intimate connection between the perception of structure, surface lightness, and illuminant.
(a) This figure produces a bistable spatial percept whose spontaneous reversal is seen to simultaneously reverse the perceived direction of illumination. (b): Isolation of one pair of panels from the figure results in a tri-stable percept, whose three states correspond to (c): a convex corner illuminated from the left, (d): a concave corner illuminated from the right, or (e): two diamond shaped tiles in the plane of the page with no percept of directed illumination. This phenomenon reveals the close coupling between the perception of structure and illumination, as well as perceived surface reflectance.
The principle of isomorphism suggests that we model the percept as it appears subjectively. The subjective experience of figure 10 b includes an awareness of a source of illumination from one side or the other, although that illuminant is perceived amodally, like the region outside the visual field. The percept is a spatial one however, as it is easy to point in the approximate direction of the perceived illumination source. We propose therefore a reverse ray-tracing algorithm that calculates a percept of the likely illumination profile from the appearance of the scene in view. Consider the case when the figure is seen as a convex corner, (figure 10 c). The "sunny side" surface would propagate a percept of bright illuminant to the left, while the "shady side" surface would propagate a perception of "dark illuminant" to the right, or the percept of reduced illumination from that direction. When the spatial configuration of the figure reverses (figure 10 d), the percept of the illumination profile is automatically reversed. In the case of the flat percept of two diamond shaped tiles (figure 10 e), both surfaces project back to the same direction of illumination and therefore their influences cancel. Since the difference in surface brightness can no longer be attributed to a difference in illumination, it must be due to surface lightness, or perceived reflectance. This explanation presupposes that each voxel or point in the volumetric representation encodes three variables at each point in an opaque surface; one for brightness, one for lightness (perceived reflectance), and one for illuminance, as described in Lehar & McLoughlin (1998).
As mentioned earlier, points on the surface of the perceptual sphere represent directions in visual space, and the connectivity of the distorted representation is such that all parallel lines meet at a point on the bounding surface of the sphere. This architecture offers a means of calculating the perceived illumination from every direction in space based on the configuration of the perceived scene. Suppose that the pattern of collinearity represented in the reference grid is designed to model the physical propagation of light through space. In other words any local element which is in the transparent state, when receiving a signal representing light from any direction, responds by passing that signal straight through the local element following the lines of collinearity defined in the perspective distorted space. This way light signals generated by a modeled light source will propagate along the curves in the representation so as to simulate the propagation of light along straight lines in Euclidean space. If a point on the surface of the perceptual sphere is designated as a light source, that light signal will propagate throughout the volume of the perceptual sphere as shown in figure 11 a. This model therefore is capable of modeling or simulating the illumination of a scene by a light source. Whenever the light signal encounters a perceived surface, i.e. elements in the opaque state, the elements representing that surface take on a surface illuminance value which is proportional to the total illumination striking that surface from any direction. A second variable of surface reflectance is also represented by every element in the opaque state, and the product of the perceived illumination and the perceived surface reflectance produces a percept of the brightness at that point on the perceived surface.
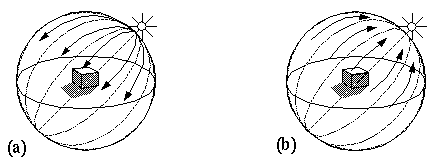
(a) A model of a perceived illumination source on the surface of the perceptual sphere propagates light signal throughout the volume of the perceptual sphere, illuminating all exposed opaque surfaces in that representation. (b) A reverse ray-tracing from every opaque surface in the space back to a percept of the illuminant apparently responsible for the observed illumination of the scene.
The ray tracing performed by the model should also operate in the reverse direction, taking the perceived surface brightness signals from every point in the scene, and propagating them backwards along the reverse light paths to produce a percept of the illumination profile. This calculation represents a spatial inference about the likely illumination profile responsible for the pattern of illuminance observed in the scene. In the scene depicted in figure 11 b for example, the illuminated surfaces which are pointing upwards to the right produce by reverse ray-tracing a percept of a bright illuminant in that direction, while the shady surfaces in the same scene project a percept of dark illuminant in the opposite direction. This description is only approximate however, because a brightly lit surface does not imply illumination exclusively from the normal direction. The illumination could actually be coming from a range of angles near the normal, so the probability distribution of the possible illuminants suggested by a bright surface defines a spherical cosine function centered on the surface normal. The global illumination profile is calculated as the sum of all such probability distributions from every surface in the scene. For example figure 12 a represents the spherical cosine illuminant distribution suggested by the bright horizontal surfaces in the scene; figure 12 b represents the illuminant distribution due to the dark vertical surfaces, which suggests darkness in the general direction of the two surface normals; figure 12 c represents the contribution of the bright vertical surfaces, invisible on the far side of the block, that produce bright peaks on the far side of the illuminant sphere, and figure 12 d represents the total illuminant percept calculated by summing all of the individual component illuminant profiles. The final perceived illumination profile therefore is only approximate, although it would clearly distinguish between a uniform v.s. a strongly polarized illumination profile. Sinha et al. (1993) propose a similar reconstruction of the global illumination profile on the surface of a Gaussian sphere. The block depicted in figures 11 and 12 is shown (for clarity) at the center of the sphere, although that point would normally be occupied by the perceptual representation of the percipient, i.e. the body percept, as in figure 9 d. However the same block displaced from the center in any direction would generate the same illuminant percept, as all parallel lines in this representation project to the same point on the surface of the representation.
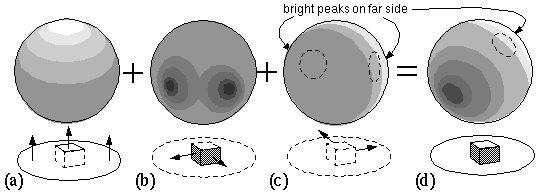
The illumination profile suggested by (a) the bright horizontal surfaces, (b) the dark vertical surfaces, (c) the bright vertical surfaces (on the far side of the block) of the scene, are summed to produce (d) the combined illumination profile suggested by the whole scene.
The forward and reverse ray tracing calculations operate simultaneously and in parallel to produce by relaxation a single globally coherent percept of both the perceived scene and the illumination profile of that scene. For example if the panels in figure 10 a or b are perceived to be part of the same surface, there will be a tendency to see them as the same lightness, or surface reflectance, even though they appear of different brightness. This tendency corresponds to the spatial diffusion of lightness signal in the lightness image that tends to unify the lightness percept within the bounds of a single gestalt. This unity however can only be achieved by assuming different illumination levels for each panel, to account for the observed difference in brightness. The different surface illuminances in the two panels in turn project, by reverse ray-tracing, two different hypotheses of the illumination strength in two different directions, producing a percept of a strongly polarized illumination profile. The illumination profile in turn projects by forward ray-tracing to illuminate the brighter panel more than the darker panel. In other words the entire percept is self-consistent, and therefore reinforces itself by positive feedback between the spatial and the illuminant percepts.
The same process in the case of the flat percept of figure 10 e produces a different result. Initially, it too might begin with an assumption of uniform lightness across both panels, which in turn projects two different illuminance signals of different strengths, but in this spatial percept the perceived panels are parallel, and so the two illuminant hypotheses are back-projected in the same direction, where the light and dark illuminant signals cancel, producing a percept of a uniform, non-polarized illumination profile. This uniform illumination in turn illuminates the two panels equally, by forward ray-tracing. This results in a conflict between the reverse ray- traced unequal illuminant, and the forward-traced equal illuminant, i.e. this time the feedback is in conflict with the initial hypothesis. As the surface illuminance signal in the two panels becomes equal, this forces a scission in the surface lightness signal to account for the difference in surface brightness. In other words the brightness assimilation between the two panels gives way to a brightness contrast between them (and assimilation within each individual panel) resulting in a percept of two uniform surfaces of different surface reflectance.
What we have described as a step-by-step process above would actually unfold in one smooth step, during which all possible interpretations of form and illuminant are pursued simultaneously, and the one that survives after feedback is the one that receives the greatest global support. The winning percept in turn suppresses the alternative interpretations by reification of its own interpretation in every surface and illuminant in the representation.
In its most general form, the model suggests that perception involves the construction of an internal spatial analog of external objects and processes. Since the spatial structures encoded in the representation emerge in response to different visual modalities, the representation itself is therefore essentially modality-independent, expressing the elements of perception in terms of objects and surfaces in the external world, rather than in terms of any particular visual modality. The lowest level of perceptual representation therefore serves as the common interface, or lingua franca between different visual properties, such as color, binocular disparity, and motion.
Figure 13 shows examples of how even a relatively simple three-dimensional scene can produce an alarmingly complex 2-D pattern of light. Factors such as the presence of multiple light sources, transparency, specular reflections, mirrored surfaces, attached shadows, cast shadows, and mutual illumination interact with one another to produce complex patterns of light that are virtually impossible to disentangle in a 2-D or 21/2-D context. Yet if such a three-dimensional scene is encoded within an internal 3-D model, those same complex patterns of shadow and shine can be readily calculated by replicating the physical propagation of light through the model. In fact figure 13 a and b were generated in exactly this manner, by a computer ray-tracing algorithm that models the complex intersecting light paths through a three-dimensional model of the scene.

(a) and (b), computer generated ray tracing images of artificial scenes, exhibiting properties of complex three-dimensional surface configurations, multiple light sources and shadow patterns, specular reflections, mirrored surfaces, attached shadows and cast shadows. (b) A photograph of a decanter on a table cloth exhibiting perception of transparency, refraction, multiple depth planes, and specular reflections.
The most difficult computational tasked faced by a computer ray-tracing algorithm is the sheer number of light rays from every point on every source that must all be traced out in all directions in sequence, as they are reflected, refracted, absorbed, and re-emitted through the various substances and surfaces in the modeled scene. This problem is addressed in our general model by proposing a parallel ray-tracing algorithm that follows all light paths simultaneously, so that the mere presence of a modeled scene in the representation automatically generates a predicted two-dimensional projection of the illumination. That complex pattern is automatically updated even as the spatial percept pops back and forth between alternative stable states. The real power of this approach is that the local behavior of individual rays of light is relatively easy to model through absorption, reflection, refraction, and re-emmission, so the complex two-dimensional projection of a scene emerges by the parallel action of a multitude of relatively simple local computations. Like a computer ray-tracing algorithm therefore, the model inherits from the properties of physical light the more complex secondary properties observed in the global pattern of light due to a visual scene. The model can therefore account for the perception of self-luminance and mutual illumination, simply by accurately modeling the propagation of light through space.
If the model accurately replicates the propagation of light, it will also automatically calculate shadows cast by opaque objects (figure 13) because the model inherits the properties of shadows from the properties of physical light. Furthermore, the model would automatically handle attached shadows, shadows cast by one object on another, and even detached shadows, for example those cast on the ground by a low flying object, even when the cast shadow falls on a broken or irregular surface. These phenomena, often problematic for more conventional image interpretation algorithms, are inherited automatically by the Gestalt Bubble model from the physical properties of light.
If the model accurately replicates a well defined localized light source, then it would also automatically replicate the behavior of a diffuse light source, that would cast fuzzy shadows instead of sharp edged shadows. Conversely, if a perception of sharp-edged shadows in a scene results, by reverse ray-tracing, in a perceptual inference of a well defined light source, a similar scene but with fuzzy shadows throughout would automatically result in a perceptual inference of a fuzzy or diffuse light source.
If the perceptual representation is endowed with color, i.e. opaque-state units and the propagating light signal are allowed to represent the additional variables of hue and saturation at every point, then a colored illumination profile will automatically result in a perceptual inference of a colored illuminant. For example if all convex objects in a scene exhibit a red highlight on one side and a blue highlight on the other, while objects perceived to be concave exhibit the reverse pattern of highlights, this would be reified by reverse ray-tracing to a percept of a red and a blue illuminant from opposite directions. Once the pattern of illumination is determined from certain surfaces in the scene, the inferred illumination will in turn help distinguish convex from concave objects in the rest of the scene based on the pattern of highlights they exhibit.
The perception of transparency, often problematic for models of perception, is again handled naturally by the Gestalt Bubble model with the minor modification of allowing matrix elements to take on intermediate values between transparent and opaque, thus allowing them to model some ratio of transmittance v.s. reflectance, as seen in figure 13 c. Also evident in that figure is the perception of mulitple depth planes, where the front and rear surfaces of the transparent carafe are seen as complete curved surfaces in front of more distant background surfaces. With another minor change, transparent objects might be modeled to deflect the modeled light passing through them, replicating another aspect of the behavior of physical light, thus accounting also for the perception of refraction, as seen in figure 13 c, where the broken contour of the table top is perceived to be actually straight and continuous, but merely distorted by refraction.
If the clear atmosphere in the perceptual sphere is given a slight blueish opacity, then the modeled light transmitted by elements in the semi-transparent state would take on a blueish tint in proportion to the distance traveled by the modeled light. More distant objects will thereby automatically tend to appear more blue than nearer objects. Conversely, a landscape of rolling green hills that become more blue with perceived distance from the observer would tend to be interpreted perceptually as as being of a uniform green, with a blue tint being attributed to the filtering effect of the semi-transparent atmosphere. Hence the blue component of an object otherwise expected to be green would serve as a cue to the distance to that object. By the simple measure of endowing the modeled atmosphere with a slight opacity therefore, this model automatically inherits a capacity to interpret the atmospheric depth cue or aerial perspective (Coren et al., 1979).
Specular reflections from polished surfaces have long been recognized as an important cue both to the shape of the illuminated object, and to the nature and direction of the illuminating light source. This property can be added to the Gestalt Bubble model by allowing opaque-state units to take on a gloss value, and by modeling glossy surfaces to reflect some proportion of incident light coherently, rather than re-emmiting it in a diffuse manner, as seen in the shiny surfaces in figure 13. A surface with 100% gloss would be modeled as a perfect mirror, coherently reflecting a whole section of the perceived scene.
Many of the perceptual phenomena addressed by this model have been deeply problematic for other computational models of perception, even when addressed individually and in isolation. While a full set of equations characterizing the present model remains to be specified, the real promise of this approach is that it is capable of addressing these most problematic issues, even where these different phenomena interact with one another to produce a very complex pattern of light. The reason is that the match between visual features encoded in perception and visual features present on the retina occurs not at the level of the sensory image, where these various influences are hopelessly confounded, but at the level of the model of physical space. That model in turn is used to generate a prediction of the complex pattern of light on the retina that would be expected from that scene, and the model is updated progressively to minimize the differences between its predicted pattern and the pattern actually present on the sensory surface. The fact that the complex scenes shown in figure 13 are perceived so effortlessly, and are perceived pre-attentively and at high spatial resolution, implicates low level perceptual processes in their interpretation. Althought the ray-tracing shown in that figure was calculated by a sequential algorithm on a digital computer, and involves exclusively forward ray-tracing to render a mathematically encoded artificial scene, the computational properties demonstrated by this algorithm illustrate exactly the kinds of phenomena that could be modeled by a parallel analog ray-tracing model operating in both forward and reverse tracing modes to match an internally modeled scene to a given visual input.
The phenomena of hallucinations and dreams demonstrate that the mind is capable of generating complete spatial percepts of the world, including a percept of the body and the space around it. It is unlikely that this remarkable capacity is used only to create such illusory percepts. More likely, dreams and hallucinations reveal the capabilities of an imaging system that is normally driven by the sensory input, generating perceptual constructs that are coupled to external reality.
Studies of mental imagery (Kosslyn 1980, 1994) have characterized the properties of this imaging capacity, and confirmed the three-dimensional nature of the encoding and processing of mental imagery. Pinker (1980) has shown that the scanning time between objects in a remembered three-dimensional scene increases linearly with increasing distance between objects in three dimensions. Shepard et al. (1971) found that the time for rotation of mental images is proportional to the angle through which they are rotated. Kosslyn also found that it takes time to expand the size of mental images, and that smaller mental images are more difficult to scrutinize (Kosslyn 1975). As unexpected as these findings may seem for theorists of neural representation, they are perfectly consistent with the subjective experience of mental imagery. On the basis of these findings, Pinker (1988) derived a volumetric spatial medium to account for the observed properties of mental image manipulation which is very similar to the model proposed here, i.e. with a volumetric azimuth/elevation coordinate system that is addressable both in subjective viewer-centered, and objective viewer-independent coordinates, and with a compressive depth scale.
The condition of hemi-neglect (Kolb et al. 1996) reveals the effects of damage to the spatial representation, destroying the capacity to represent spatial percepts in one half of phenomenal space. Such patients are not simply blind to objects to one side, but are blind to the very existence of a space in that direction as a potential holder of objects. For example, neglect patients will typically eat food only from the right half of their plate, and express surprise at the unexpected appearance of more food when their plate is rotated 180 degrees. This condition even persists when the patient is cognitively aware of their deficit (Sacks 1985) and can also impair mental imaging ability. Bisiach et al. (1978,1981) describe a neglect patient who, when instructed to recall a familiar scene viewed from a certain direction, recalls only objects from the right half of his remembered space. When instructed to mentally turn around and face in the opposite direction, the patient now recalls only objects from the other side of the scene, that now fall in the right half of his mental image space. The condition of hemi-neglect therefore suggests damage to one half of a three-dimensional imaging mechanism that is used both for perception and for the generation of mental imagery. Note that hemi-neglect also includes a neglect of one side of the body, which is consistent with the fact that the body percept is included as an integral part of the perceptual representation. Whatever the physiological reality behind the phenomenon of hemi-neglect, the Gestalt Bubble model offers at least a concrete description of this otherwise paradoxical phenomenon.
The idea that this spatial imaging system employs an explicit volumetric spatial representation is suggested by the fact that disparity tuned cells have been found in the cortex (Barlow et al. 1967), as predicted by the Projection Field Theory of binocular vision (Kaufman 1974, Boring 1933, Charnwood 1951, Marr et al. 1976, Julesz 1971), which is itself a volumetric model. Psychophysical evidence for a volumetric representation comes from the fact that perceived objects in depth exhibit attraction and repulsion in depth (Westheimer et al. 1987, Mitchison 1993) in a manner analogous to the center-surround processing in the retina. Brooks et al. (1989) discussed this analogy and show that a number of brightness illusions that have been attributed to such center-surround processing have corresponding illusions in depth. Similarly, Anstis et al. (1978) demonstrated a Craik-O'Brien-Cornsweet illusion in depth by cutting the near surface of a block of wood with a depth profile matching the brightness cusp of the brightness illusion, resulting in an illusory percept of a difference in depth of the surfaces on either side of the cusp. As in the brightness illusion, therefore, the depth difference at the cusp appears to propagate a perceptual influence out to the ends of the block, suggesting a spatial diffusion of depth percept between depth edges.
The many manifestations of constancy in perception have always posed a serious challenge for theories of perception because they reveal that the percept exhibits properties of the distal object rather than the proximal stimulus, or pattern of stimulation on the sensory surface. The Gestalt Bubble model explains this by the fact that the information encoded in the internal perceptual representation itself reflects the properties of the distal object rather than the proximal stimulus. For example the internal percept reflects the intrinsic reflectance of a surface rather than (or in addition to) its brightness on the retinal image, as demonstrated by Rock et al. (1992) who show that grouping by similarity is based on perceived lightness after the achievement of constancy, and not on the brightness of the elements at the level of the proximal stimulus. Size constancy is explained by the fact that objects perceived to be more distant are represented closer to the outer surface of the perceptual sphere, where the collapsing reference grid corrects for the shrinkage of the retinal image due to perspective. An object perceived to be receding in depth therefore is expected perceptually to shrink in retinal size along with the shrinking of the grid in depth. This explains why shrinking objects tend to be perceived as receding. Rock et al. (1964), showed that perceptual grouping by proximity is determined not by proximity in the two-dimensional retinal projection of the figure, but rather by the three-dimensional perceptual interpretation. A similar finding is shown by Green et al. (1986). Shape constancy is exemplified by the fact that a rectangle seen in perspective is not perceived as a trapezoid, as its retinal image would suggest. The Müller-Lyer and Ponzo illusions are explained in similar fashion (Tausch 1954, Gregory 1963, Gillam 1970), the converging lines in those figures suggesting a surface sloping in depth, so that features near the converging ends are measured against a more compressed reference grid than the corresponding feature near the diverging ends of those lines.
Several researchers have presented psychophysical evidence for a spatial interpolation in depth, which is difficult to account for except with a volumetric representation in which the interpolation is computed explicitly in depth (Attneave 1982). Kellman et al. (1996) have demonstrated a coplanar completion of perceived surfaces in depth in a manner analogous to the collinear completion in the Kanizsa figure. Barrow et al. (1981, p. 94 and figure 6.1) showed how a two-dimensional wire-frame outline held in front of a dynamic random noise pattern stimulates a three-dimensional surface percept spanning the outline like a soap film, and that perceived surface undergoes a Necker reversal together with the perceived reversal of the perimeter wire. Ware et al. (1978) have shown that a three-dimensional rendition of the Ehrenstein illusion constructed of a set of rods converging on a circular hole, creates a three-dimensional version of the illusion that is perceived as a spatial structure in depth, even when rotated out of the fronto-parallel plane, complete with a perception of brightness at the center of the figure. This illusory percept appears to hang in space like a faintly glowing disk, reminiscent of the neon color spreading phenomenon. A similar effect can be achieved with a three-dimensional rendition of the Kanizsa figure.
Carman et al. (1992) employed a depth probe to measure the perceived depth of three-dimensional illusory surfaces seen in Kanizsa figure stereograms, whose inducing edges are tilted in depth in a variety of configurations (figure 14 a). Note how the illusory surface completes in depth by coplanar interpolation defining a smooth curving surface. The subjects in this experiment reported a flexing of the perceived surface in depth near the depth probe. Equally interesting is the "port hole" illusion seen in the reverse-disparity version of this figures, where the circular completion of the port holes generates an ambiguous unstable semi-transparent percept at the center of the figure. Kellman et al. (1991) and Idesawa (1991) report the emergence of more complex illusory surfaces in depth, using similar illusory stereogram stimuli as shown in figure 14 b and c. It is difficult to deny the reality of a precise high-resolution spatial interpolation mechanism in the face of these compelling illusory percepts.
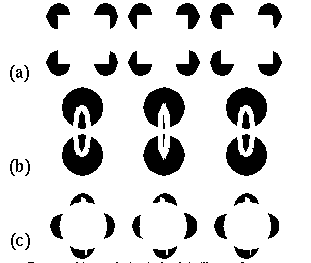
Perceptual interpolation in depth in illusory figure stereograms, adapted from (a) Carman et al. (1992), (b) Kellman et al. (1991), and (c) Idesawa (1991). Opposite disparity percepts are achieved by binocular fusion of either the first and second, or the second and third columns of the figure.
Evidence of a close dynamic coupling between parallel low-level visual features is seen in cross-modal integration effects, in which a feature present only in one visual modality influences a corresponding low-level percept in a different modality. Such cross-modal integration has been reported between the perception of transparency, depth, luminance, and subjective contours (Nakayama et al. 1990), parametric variation in one modality being observed to influence the low-level perception of the others. Nakayama et al. (1990) conclude that "there appears to be strong coupling between the dimensions of depth, color, and luminance, indicating interaction rather than segregation. So it is possible that the segregation of pathways seen in anatomical and physiological studies could be misleading if considered in isolation". Anstis et al. (1978) report how their Craik- O'Brien-Cornsweet depth illusion is experienced as a haptic sensation when the block of wood is held by its ends, far from the inducing depth cusp observed visually at the middle of the block, showing that the visual illusion promotes a corresponding tactile or haptic illusion. The McGurk effect (McGurk et al. 1976) exemplifies how a visual stimulus can alter the immediate auditory experience of a speech sound. Gilchrist (1977, Gilchrist et al. 1983) Knill (1991) and Adelson (1993) have shown how the perception of three-dimensional structure influences the perceived lightness and illumination of a scene.
Evidence for the spherical nature of perceived space dates back to observations by Helmholtz (1925) [*** Veith Müller ***]. A subject in a dark room is presented with a horizontal line of point-lights at eye level in the frontoparallel plane, and instructed to adjust their displacement in depth, one by one, until they are perceived to lie in a straight line in depth. The result is a line of lights that curves inwards towards the observer, the amount of curvature being a function of the distance of the line of lights from the observer. Helmholtz recognized this phenomenon as evidence of the non-Euclidean nature of perceived space. The Hillebrand-Blumenfeld alley experiments (Hillebrand 1902, Blumenfeld 1913) extended this work with different configurations of lights, and mathematical analysis of the results (Luneburg 1950, Blank 1958) characterized the nature of perceived space as Riemannian with constant Gaussian curvature (see Graham 1965 and Foley 1978 for a review). In other words, perceived space bows outward from the observer, with the greatest distortion observed proximal to the body, as suggested by the Gestalt Bubble model. Heelan (1983) presents a more modern formulation of the hyperbolic model of perceived space, and provides further supporting evidence from art and illusion.
It is perhaps too early to say definitively whether the proposed model can be formulated to address all of the phenomena outlined above. What is clear is the inadequacy of the simple feed-forward abstraction approach to account for these phenomena. The general solution offered by our model is based on the following ideas, (1) the internal perceptual representation encodes properties of the distal object rather than of the proximal stimulus, (2) the computations of spatial perception are most easily performed in a fully spatial matrix, (3) the complementary operations of abstraction and reification serve to extract central tendencies, which are then used to reconstruct peripheral details by reification, in a manner consistent with the subjective experience of perception. The multistability of perception suggests that a great multitude of factors weigh in to determine the final perceptual state.
An elaborate model of perception has been presented that incorporates many of the concepts and principles introduced by the original Gestalt movement. While the actual mechanisms of the proposed model remain vague, this model, or modeling approach makes the following predictions:
That when a person views a three-dimensional surface, their subjective experience of that surface simultaneously encodes every point on that surface in three dimensions, at a high resolution. In other words, our subjective experience of the world around us is not of a flattened "21/2-D sketch", nor of a non-spatial abstraction, but of a solid spatial world that appears to surround us in all directions.
That volumes of empty space are perceived with the same geometrical fidelity as volumes of solid matter.
That multiple transparent surfaces can be perceived simultaneously as distinct spatial structures at high resolution.
That the infinity of external space is perceived as a finite, but fully spatial representation which appears near-Euclidean near the body, but becomes progressively flattened with distance from the body, the entire percept being bounded by a spherical shell representing perceptual infinity.
That parallel lines are perceived to meet at perceptual infinity, while at the same time they are perceived as parallel and with uniform separation throughout their entire length.
That an illusory entity, like the Kanizsa figure, or the apparent motion illusion, is not experienced as a cognitive abstraction, but is experienced perceptually as a solid spatial surface at high resolution, virtually indistinguishable from a real physical surface or object.
That the subjective reversal of a multistable percept is not experienced as a change in a cognitive interpretation, or the flipping of a single cognitive variable, but is vividly experienced as an inversion of a perceptual data structure, changing the perceived depth of every point on the perceived structure.
That the perception of space extends outside the visual field into the space behind the head.
That the hidden rear surfaces of objects are perceived amodally as a structure in depth.
That the perception of a lighted object stimulates an amodal percept of an illumination source.
Most of these "predictions" are immediately manifest in the subjective experience of perception. Curiously, these obvious properties of perception have been ignored by most neural modelers, even though their central significance was highlighted decades ago by the Gestaltists. There are two main reasons why these prominent aspects of perception have been consistently ignored. The first results from the outstanding success of the single-cell recording technique, which has shifted our theoretical emphasis from field-like theories of perception, to point-like theories of the elements of neural computation. Like the classical introspectionists who refused to acknowledge perceptual experiences that were inconsistent with their preconceived notions of sensory representation, the neuroreductionists of today refuse to consider aspects of perception that are inconsistent with current theories of neural computation.
Similarly, most contemporary researchers ignore the fact that the world we perceive around us is an illusion, because the illusion is so compelling that it is easy to mistake the percept of the world for the real world itself. And yet this Naïve Realist view that we can somehow perceive the world directly, is inconsistent with the physics of perception (Russell 1927, Köhler 1971). If perception is a consequence of neural processing of the sensory input, a percept cannot in principle escape the confines of our head to appear in the world around us, any more than a computation in a digital computer can escape the confines of the computer. We cannot therefore in principle have direct experience of objects in the world itself, but only of the internal effigies of those objects generated by mental processes. The world we see around us therefore can only be an elaborate, though very compelling illusion, which must in reality correspond to perceptual data structures and processes occurring within our own head. This picture-in-the-head or Cartesian theatre view of perception has been criticized on the grounds that there would have to be a miniature observer to view this miniature internal scene, resulting in an infinite regress of observers within observers. Pinker (1984, p. 38) points out however that there is no need for an internal observer of the scene, since the internal representation is simply a data structure in spatial form. The reason for this spatial form is to enable spatial calculations on that data. The little man at the center of this spherical world therefore is not a miniature observer of the internal scene, but is itself a spatial percept, constructed of the same perceptual material as the rest of the spatial scene, for that scene would be incomplete without a replica of the percipient's own body in his perceived world.
As soon as we examine the world we see around us, not as a physical scientist observing the physical world, but as a perceptual scientist observing a rich and complex internal percept, only then does the rich spatial nature of perceptual processing become immediately apparent. It was this central insight into the illusion of consciousness that formed the key inspiration of the Gestalt movement (Koffka 1935 p.27-36, Köhler 1971) from which all of their other ideas were developed. It is in this context that the elaborate model presented here begins to seem plausible.
Adelson E. 1993 "Perceptual Organization and the Judgement of Brightness" Science 262 2042-2044
Adelson E. & Pentland A. P. 1996 The Perception of Shading and Reflectance. In D. Knill & W. Richards (Eds.) Perception as Baysian Inference. New York: Cambridge University Press.
Anstis S. & Howard I, 1978 "A Craik-O'Brien-Cornsweet Illusion for Visual Depth" Vision Research 18 213-217.
Arnheim R. 1969a Art and Visual Perception: A Psychology of the Creative Eye. Berkeley, University of California Press.
Arnheim R. 1969b Visual Thinking. Berkeley, University of California Press.
Attneave F. 1955a " Symmetry, Information, and Memory for Patterns". American Journal of Psychology 68 209-22.
Attneave F. 1955b "Perception of Place in a Circular Field". American Journal of Psychology 68 69-82.
Attneave F. 1982 "Prägnanz and soap bubble systems: a theoretical exploration" in Organization and Representation in Perception, J. Beck (Ed.), Hillsdale NJ, Erlbaum.
Attneave F. & Farrar P. 1977 "The Visual World Behind the Head". American Journal of Psychology 90 (4) 549-563.
Barlow H., Blakemore C., & Pettigrew J. 1967 "The Neural Mechanism of Binocular Depth Discrimination". Journal of Physiology 193 327-342.
Barrow H. G. & Tenenbaum J. M. 1981 Interpreting Line Drawings as Three Dimensional Surfaces. Artificial Intelligence 17, 75-116.
Biederman I. 1987 "Recognition-by-Components: A Theory of Human Image Understanding". Psychological Review 94 115-147
Bisiach E. & Luzatti C. 1978 "Unilateral Neglect of Representational Space". Cortex 14 129-133.
Bisiach E., Capitani E., Luzatti C., & Perani D. 1981 "Brain and Conscious Representation of Outside Reality". Neuropsychologia 19 543-552.
Blank A. A. 1958 Analysis of Experiments in Binocular Space Perception. J. Opt. Soc. Amer., 48 911-925.
Blum 1973 "Biological Shape and Visual Science (Part I)". Journal of Theoretical Biology 38 205-287.
Blumenfeld W. 1913 "Untersuchungen Über die Scheinbare Grösse im Sehraume". Z. Psychol., 65 241-404.
Boring 1933 "The Physical Dimensions of Consciousness". New York: Century.
Bressan P. 1993 "Neon colour spreading with and without its figural prerequisites" Perception 22 353-361
Brookes A. & Stevens K. 1989 "The analogy between stereo depth and brightness". Perception 18 601-614.
Carman G. J., & Welch L. 1992 "Three-Dimensional Illusory Contours and Surfaces". Nature 360 585-587.
Charnwood J. R. B. 1951 "Essay on Binocular Vision". London, Halton Press.
Collett T. 1985 "Extrapolating and Interpolating Surfaces in Depth". Proc. R. Soc. Lond. B 224 43-56.
Coren S. 1972 "Subjective Contours and Apparent Depth" Psychological Review 79 359-367
Coren S., Ward L. M., & Enns J. J. 1979 "Sensation and Perception". Ft Worth TX, Harcourt Brace.
Cornsweet T. N. 1970 "Visual Perception". New York, Academic Press.
Fischler M. A. & Leclerc Y. G. 1992 Recovering 3-D Wire Frames from Line Drawings. Proceedings of the Image Understanding Workshop.
Foley J. M. 1978 "Primary Distance Perception".In: Handbook of Sensory Physiology, Vol VII Perception. R. Held, H. W. Leibowitz, & HJ. L. Tauber (Eds.) Berlin: Springer Verlag, pp 181-213.
Garner 1974 "The Processing of Information and Structure". Potomac MD: Erlbaum.
Geldard F. A. & Sherrick C. E. 1972 "The Cutaneous Rabbit: A Perceptual Illusion". Science 178 178-179.
Gilchrist A, 1977 "Perceived lightness depends on perceived spatial arrangement" Science 195 185-187
Gilchrist A., Delman S., Jacobsen A. 1983 "The classification and integration of edges as critical to the perception of reflectance and illumination" Perception & Psychophysics 33 425-436
Gillam, B. 1980 "Geometrical Illusions". Scientific American 242 102-111.
Graham C. H. 1965 Visual Space Perception. in C. H. Graham (Ed.) Vision and Visual Perception, New York, John Wiley 504-547.
Green M. & Odum V. J. 1986 "Correspondence Matching in Apparent Motion: Evidence for Three Dimensional Spatial Representation". Science 233 1427-1429.
Gregory R. L. 1963 "Distortion of Visual Space as Inappropriate Constancy Scaling." Nature 199, 678-679.
Grossberg S, Mingolla E, 1985 "Neural Dynamics of Form Perception: Boundary Completion, Illusory Figures, and Neon Color Spreading" Psychological Review 92 173-211
Grossberg S, Todorovic D, 1988 "Neural Dynamics of 1-D and 2-D Brightness Perception: A Unified Model of Classical and Recent Phenomena" Perception and Psychophysics 43, 241-277
Heckenmuller E. G. 1965 "Stabilization of the Retinal Image: A Review of Method, Effects, and Theory". Psychological Bulletin 63 157-169.
Heelan P. A. 1983 "Space Perception and the Philosophy of Science" Berkeley, University of California Press.
Helmholtz H. 1925 "Physiological Optics" Optical Society of America 3 318.
Hillebrand F. 1902 "Theorie der Scheinbaren Grösse bei Binocularem Sehen". Denkschr. Acad. Wiss. Wien (Math. Nat. Kl.), 72 255-307.
Hochberg J. & Brooks V. 1960 "The Psychophysics of Form: Reversible Perspective Drawings of Spatial Objects". American Journal of Psychology 73 337-354.
Hollingsworth-Lisanby S., Lockhead G. R. 1989 "Subjective Randomness, Aesthetics, and Structure". In G. R. Lockhead & J. R. Pomerantz (Eds.) The Perception of Structure. Washington DC, American Psychological Association, 97-114.
Idesawa M. 1991 "Perception of 3-D Illusory Surfaces with Binocular Viewing. Japanese Journal of Applied Physics 30 (4B) L751-L754.
Julesz B. 1971 "Foundations of Cyclopean Perception". Chicago, University of Chicago Press.
Kanizsa G, 1979 "Organization in Vision" New York, Praeger.
Kaufman 1974 "Sight and Mind". New York, Oxford University Press.
Kellman P. J., & Shipley T. F. 1991 "A Theory of Visual Interpolation in Object Perception". Cognitive Psychology 23 141-221.
Kellman P. J., Machado L. J., Shipley T. F., & Li C. C. 1996 "Three-Dimensional Determinants of Object Completion. Annual Review of Vision and Ophthalmology (ARVO) abstracts, 3133 37 (3) p. S685.
Knill D. & Kersten D. 1991 "Apparent surface curvature affects lightness perception" Nature 351 228-230
Kolb B. & Whishaw I. Q. 1996 "Fundamentals of Human Neuropsychology". W. H. Freeman, p. 247-276.
Koffka K. 1935 "Principles of Gestalt Psychology. New York, Harcourt Brace, Chapter III)
Köhler W. 1971 "An Old Pseudoproblem". In M. Henle (Ed.) The Selected Papers of Wolfgang Köhler. New York, Liveright, 125-141.
Kosslyn S. M. 1975 "Information Representation in Visual Images." Cognitive Psychology 7 341-370.
Kosslyn S. M. 1980 "Image and Mind" Cambridge MA, Harvard University Press.
Kosslyn S. M. 1994 "Image and Brain: The Resolution of the Imagery Debate". Cambridge MA, MIT Press.
Kovács I, & Julesz B. 1995 "Psychophysical Sensitivity Maps Indicate Skeletal Representation of Visual Shape". Perception Supplement 24 34.
Kovács I., Fehér Á., & Julesz B. 1997 "Medial Point Description of Shape: A Representation for Action Coding and its Psychophysical Correlates". Rutgers Center for Cognitive Science, TR-33.
Lehar S. 1994 "Directed Diffusion and Orientational Harmonics: Neural Network Models of Long-Range Boundary Completion through Short-Range Interactions". Ph.D. Thesis, Boston University.
Lehar S. & McLoughlin N. 1998 "Gestalt Isomorphism I: Emergence and Feedback in the Perception of Lightness, Brightness, and Illuminance. Perception (submitted).
Luneburg R. K. 1950 "The Metric of Binocular Visual Space". J. Opt. Soc. Amer., 40 627-642.
Marr D, 1982 "Vision". New York, W. H. Freeman.
Marr D. & Poggio T. 1976 "Cooperative Computation of Stereo Disparity". Science 194 283-287.
Marr D. 1977 "Representing Visual Information". A. I. Memo 415, A. I. Lab, Massachusetts Institute of Technology.
McGurk H. & MacDonald J. 1976 "Hearing Lips and Seeing Voices". Nature 264 746-748
McLoughlin N. & Grossberg S. 1998 "Cortical Computation of Stereo Disparity". Vision Research 38 91-99
Michotte A, 1963 "The Perception of Causality". Translated by T. and E. Miles from French (1946) edition. London: Methuen.
Mitchison G, 1993 "The neural representation of stereoscopic depth contrast" Perception 22 1415-1426
Movshon J. A., Adelson E. H., Gizzi M. S., & Newsome W. T. 1986 "The Analysis of Moving Patterns". In C. Chagas, R. Gattass, & C. Cross (Eds.) Pattern Recognition Mechanisms, 112-151. Berlin: Springer Verlag.
Nakayama K, Shimojo S, Ramachandran V, 1990 "Transparency: relation to depth, subjective contours, luminance, and neon color spreading" Perception 19 497-513
Palmer S. E. 1985 "The Role of Symmetry in Shape Perception". Acta Psychologica 59 67-90.
Pinker S. 1980 "Mental Imagery and the Third Dimension". Journal of Experimental Psychology 109 354-371.
Pinker S. 1984 "Visual Cognition: An Introduction". Cognition 18 1-63.
Pinker S. 1988 "A Computational Theory of the Mental Imagery Medium". In: M. Denis, J. Engelkamp, J. T. E. Richardson (Eds.) Cognitive and Neuropsychological Approaches to Mental Imagery. Boston, Martinus Nijhoff.
Psotka J. 1978 "Perceptual Processes That May Create Stick Figures and Balance". Journal of Experimental Psychology: Human Perception & Performance 4 101-111.
Ramachandran V. S. & Anstis S. M. 1986 "The Perception of Apparent Motion". Scientific American 254 80-87.
Ramachandran V. S. 1992 "Filling in Gaps in Perception: Part 1" Current Directions in Psychological Science 1 (6) 199-205
Ramachandran V. S. 1994 " Phantom Limbs, Neglect Syndromes, Repressed Memories, and Freudian Psychology". International Review of Neurobiology 37 291-333.
Reed E. S. (1988) "James J. Gibson and the Psychology of Perception". New Haven CT, Yale University Press.
Rock I, & Brosgole L. 1964 "Grouping Based on Phenomenal Proximity" Journal of Experimental Psychology 67 531-538.
Rock I, Nijhawan R., & Palmer S. 1992 "Grouping Based on Phenomenal Similarity of Achromatic Color" Perception 21 (6) 779-789.
Russell B. 1927 Physical and Perceptual Space. In B. Russell Philosophy, New York, W. W. Norton 137-143.
Sacks, O. 1985 "The Man Who Mistook His Wife For a Hat". New York, Harper & Row. p. 77-79
Shepard R. N. & Metzler J. 1971 "Mental Rotation of Three-Dimensional Objects". Science 171 701-703.
Sinha P. & Adelson E. 1993 "Recovering Reflectance and Illumination in a World of Painted Polyhedra" Proceedings Fourth International Conference on Computer Vision, Berlin. 156-163.
Takeichi H, Watanabe T, Shimojo S, 1992 "Illusory occluding contours and surface formation by depth propagation". Perception 21 177-184
Tampieri G. 1956 "Sul Completamento Amodale di Rappresentazioni Prospettiche di Solidi Geometrici". Atli dell' XI Congresso Degli Psicologi Italiani, ed. L. Ancona, pp 1-3 Milano: Vita e Pensiero.
Tausch, R. 1954 "Optische Täuschungen als artifizielle Effekte der Gestaltungs-prozesse von Grössen und Formenkonstanz in der natürlichen Raumwahrnehmung". Psychologische Forschung, 24, 299-348.
Taya R., Ehrenstein W. H., & Cavonius C. R. 1995 "Varying the Strength of the Munker-White Effect by Stereoscopic Viewing". Perception 24 685-694.
Ullman S. 1984 Maximizing Rigidity: the incremental recovery of 3-D structure from rigid and nonrigid motion. Perception 13, 255-274.
Ware C. & Kennedy J. M. 1978 "Perception of Subjective Lines, Surfaces and Volumes in 3-Dimensional Constructions". Leonardo 11 111-114.
Westheimer G. & Levi D. M. 1987 "Depth Attraction and Repulsion of Disparate Foveal Stimuli". Vision Research 27 (8) 1361-1368.
Yarbus A. L. 1967 "Eye Movements and Vision". New York: Plenum Press.
The appendix of this paper is essentially identical to that in my other Isomorphism paper which was a later development of this one.