Seth Cameron
Submitted to Spatial Vision
Rejected July 1994
Whether designing animals, insects, or plants, Nature draws upon symmetry and periodicity to play a fundamental role in defining the body plan. When implemented with the proper chemical mechanisms, these principles guide our bodies from single-celled embryos to bilaterally symmetric creatures with intricate periodic structures, such as the spine and rib cage. The properties of symmetry and periodicity also appear to be fundamental to visual perception. We will show that this is no coincidence, but is a consequence of the fact that these properties are generated by the same underlying phenomenon, standing wave patterns formed from harmonic resonances. The symmetry in life forms arises from chemical harmonic resonances, whereas the symmetry in visual perception arises from harmonic resonances in the visual system. We will show that harmonic resonances have very interesting properties for the representation of geometrical form that make them eminently suitable for encoding geometric form for body plans as well as for visual perception. In particular, we will show that by being simultaneously invariant to perspective transformation and robust to deformation, such resonant representations have fundamental advantages over more traditional techniques.
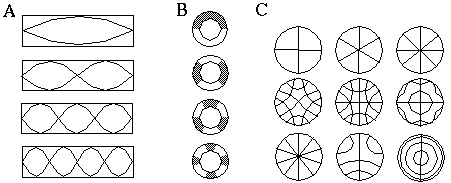
Harmonic resonances are a natural property of all physical systems. They are seen in the vibration of elastic solids, acoustical harmonics in resonant cavities, harmonic oscillations in electrical and electronic circuits, lasing and masing in electromagnetic radiation, and even in chemical reactions in the form of reaction diffusion. A fundamental property of all such harmonics is that they tend to divide the resonating body into integer numbers of equal intervals in a periodic or symmetrical pattern. For example, Figure 1 (A) shows the patterns of acoustical oscillation in a closed tubular cavity as it resonates to the first, second, third, and fourth harmonics. This figure could also be considered as a depiction of the modes of oscillation of an elastic rod. Figure 1 (B) illustrates the corresponding acoustical harmonics in a circular tube, or vibrational harmonics in a ring which likewise subdivides the circle into segments of equal angular extent. Unlike in the case of the linear harmonics which are fixed by the boundary conditions at the ends of the tube, the circular harmonics depicted in Figure 1 (B) can occur at any orientation. Moreover, the patterns due to harmonic oscillation are not always a simple linear periodicity. Chladni [2] showed how a steel plate that is set into harmonic oscillations by bowing it with a violin bow can exhibit a large variety of harmonic modes whose geometrical patterns can be revealed by a sprinkling of sand, which collects at the nodes of vibration. Figure 1 (C) illustrates just some of the many figures that occur in a circular plate bowed in this manner. Notice that a fundamental property of the Chladni figures is a periodicity either in radial, circumferential, or other dimension, which translates to various forms of symmetry.

Harmonic resonances in a linear tube or rod (A), in a circular tube or ring (B), and in a circular plate (C).
Chemical harmonic resonances are responsible for defining geometrical patterns in the body forms of animals and plants. Turing [19] presented a pioneering analysis of the principle behind such chemical harmonics. Given two reagents which are mixed in a chemical bath, he showed that periodic patterns of chemical concentration will spontaneously arise under certain reaction and diffusion conditions. The reaction conditions involve a catalytic interaction between the two reagents, where the equilibrium concentration is the result of a dynamic balance that emerges even while the reactions continue unabated, converting one reagent into the other at the same rate that the other is transformed continuously into the first. The diffusion condition requires that the rate of diffusion of one reagent in the chemical bath be greater than that of the other. Although the mathematics is rather complex, the principle can be illustrated with a simple analogy. Consider a population of predators and prey. The greater the concentration of prey in any one area, the greater will be their rate of self replication by reproduction. This will tend to exponentially amplify any irregularities in the initial distribution. A concentration of prey will however attract a population of predators that exert a dynamic limit to prey population. Imagine now that the prey are rodents and the predators are wild dogs, so that the prey "diffuse" more slowly in their daily wanderings than the predators, who have a greater range of travel. A local concentration of rodents will support a population of dogs centered at that same location, but ranging out over a wider area. This will tend to suppress adjacent populations of rodents, so that the next adjacent concentration of rodents will typically be found beyond a certain distance from the first. In a continuous mathematical model this will result in a periodic distribution of predators and prey, with isolated concentrations of prey surrounded by regions consisting almost exclusively of predators. The pattern of distribution will be influenced by the topography. On a long thin island or peninsula the population will define a periodic banded pattern, like the pattern of harmonic resonances in a linear tube, while on a circular island the patterns define periodic spots or patches. Under the right conditions these patches can exhibit symmetries that resemble the Chladni figures.
This kind of reaction diffusion has been reproduced in the test tube in the Belousov-Zhabotinskii reaction [20] which produces a dynamic striped pattern along the length of the tube, that changes continuously through time while maintaining the same general periodicity. Murray [14, 15] has suggested that similar reaction diffusion interactions are responsible for the patterns of markings on animal coats, and has shown that a small change in parameters can alter the pattern from leopard spots through giraffe patches to tiger and zebra stripes. This model explains for example why the spotted pattern in most spotted animals becomes a ringed pattern at the tip of the tail, by the same principle that a spotted concentration of predator and prey on a circular island will transform to a striped pattern on a long thin peninsula of the island. Kauffman [11] proposes that a similar reaction diffusion is responsible for the periodic segmentation in the body plan of insects. Specific cells in the early embryo release certain morphogens which mark one end of the embryo as the head, and the other end as the tail. Figure 2 (A) suggests schematically how the chemical concentration of such morphogens released at the head and the tail might disperse through the embryo by passive diffusion. The influence of reaction diffusion on this initial concentration gradient would be to sharpen the contrast between the two concentrations, producing an equilibrium concentration pattern more like Figure 2 (B). As in the case of acoustical resonance, such reaction diffusion systems can exhibit different harmonics, depending on the rates of reaction and diffusion of the various morphogens. Under different conditions therefore, the same disposition of head and tail morphogen releasing cells could define a pattern of concentration as shown in Figure 2 (C), or higher harmonics. The cells which release the morphogens therefore serve to anchor the pattern, but the pattern itself is determined by reaction diffusion. Murray suggests that different morphogens act simultaneously in the same embryo but at different harmonic frequencies. For example, Figure 2 (D) shows a first harmonic pattern due to one morphogen, a second harmonic pattern due to a different morphogen, and a fourth harmonic pattern due to a third morphogen. If all three of these morphogenic patterns are present simultaneously in the embryo, any cell in the embryo would know its exact location simply by the presence or absence of each of the three morphogens. The three morphogens in effect define a binary map of location within the embryo, as suggested in Figure 2 (E), where each bit of the binary code represents the presence or absence of one of the three morphogens. The morphogens in turn serve to activate or deactivate the expression of particular genes within their segment, dictating for example that one segment should develop legs, while another develops antennae, etc.. A similar harmonic interaction in early embryonic development is responsible for the periodicity seen in the human ribs and spinal chord.
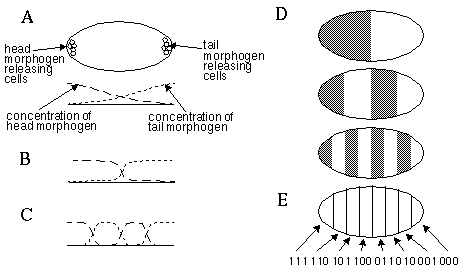
Chemical concentration gradient of morphogens released by specific cells due to passive diffusion through the embryo (A), and the influence of chemical harmonic resonances on the concentration
Newman [17] proposes that another harmonic resonance is involved in the development of embryonic wing of the chicken. The wing begins as a hemispheric limb bud on the chick embryo as shown schematically in Figure 3 (A), and a concentric harmonic resonance within the limb bud differentiates the central tissue, as shown in the cross section, determining that tissue to develop eventually into bone. This will become the humerus, or upper wing bone. As the limb bud grows in physical size and begins to take on an elliptical cross section, the pattern breaks abruptly into a second harmonic mode, generating a double core of bone, leaving a bifurcating trail of bone tissue, as shown in Figure 3 (B). This double bone defines the radius and ulna, or lower wing bones. Finally the pattern breaks into a third harmonic mode, leaving a trifurcating trail of bone tissue, as shown in Figure 3 (C), corresponding to the three digits of the chicken wing. The harmonic resonance need only be present during a brief critical period of development, but its influence on the subsequent development of the embryonic cells is permanent. This models explains why the limbs of animals generally exhibit a single bone proximally, and increasing numbers of bones as one progresses distally, as is seen in the human arm and leg bones.
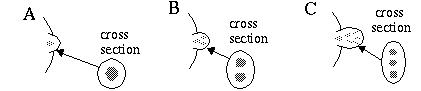
First harmonic (A), second harmonic (B), and third harmonic (C) chemical resonance which defines the geometry of the single upper wing bone, double lower wing bones, and triple digits in developing chick
The use of harmonic resonances as an architectural blueprint of geometrical form has very interesting consequences. Unlike a blueprint used in engineering, the harmonic representation is remarkably flexible and adaptive, automatically compensating for any irregularities in the tissue. The periodic boundaries depicted in Figure 2 (C) are not defined by measurement from some fixed reference point, as is the practice in mechanical engineering, but rather are determined by a dynamic interaction involving the volume of the tissue. This makes the architectural plan adaptive to deformations in the embryonic tissue. Figure 4 (A) shows how the periodic banded pattern of the embryonic insect might respond to a deformation in the geometry of the embryo by generating segments of equal volume but dissimilar geometry. When the geometrical distortion exceeds some limit, the pattern will abruptly break into a different mode, generating discrete new features, as suggested in Figure 4 (B). It is this property of harmonic resonances that accounts for the remarkable adaptability and resistance to distortion observed in morphological development. Wolpert [21] describes a series of experiments which demonstrate this adaptability in the development of the embryonic chick wing. The three digits of the wing are not actually symmetrical, as suggested in Figure 3, but as in other birds the "thumb" is considerably shorter, as shown in Figure 4 (C). The orientation of this asymmetry is established by a small group of cells at the anterior end of the limb bud which release a particular morphogen. During a critical stage of development Wolpert grafted such cells from one embryo into a limb bud of another embryo posterior to the original cells, producing wings such as those shown in Figure 4 (D) and (E). What is remarkable in these mutations is that when the global pattern of the limb is made to bifurcate unnaturally, all of the muscles, tendons, nerves and blood vessels also bifurcate as if this were part of the original design. A similar phenomenon is seen in Siamese twins and other natural malformations. This kind of remarkable adaptability in the body plan is a fundamental property of the harmonic representation which is unparalleled by any scheme or system used in human engineering.
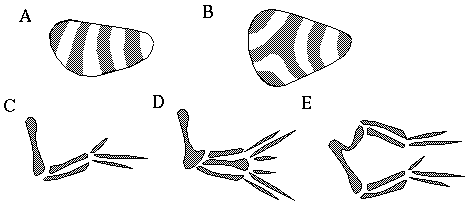
Deformation of the periodic pattern defined by chemical harmonics in response to deformations in the embryo (A) and (B); pattern of bones in chick wing (C), and deformations caused by disruption of chemical harmonic resonance (D) and (E).
Symmetry has long been recognized as an important organizational principle in visual perception. The Gestalt psychologists listed symmetry and periodicity along with similarity, proximity, good continuation, and a number of other properties as fundamental to perception. Bilateral symmetry in the Rorschach ink blot tests seems to give meaning to otherwise random blobs of ink, which are seen by subjects as human and animal body forms, faces, etc. This phenomenon is partly due to the bilateral symmetry which is naturally inherent in biological forms, but it also reveals an inclination towards symmetry in visual perception. That inclination is also apparent in the patterns seen in a kaleidoscope, where random patterns are replicated with multi-fold symmetry to become more meaningful and pleasing to the eye. Finally, symmetry and periodicity are ubiquitous in art and architecture. Much of the symmetry seen in art is simply a reflection of symmetry in nature, especially in the case of plant or animal motifs. If however one studies the difference between a representational piece of art and the natural object that it represents, the art work is often exaggerated in its symmetry. This is especially true in heraldic or symbolic representations, such as the American eagle, the British lion, the Tudor rose, the Fleur de Lys, corporate logos, religious icons, etc. Some of the symmetry seen in architecture has a functional origin, due to the fact that symmetrical forms often have greater strength, and can be constructed of identical modular units. However, the frivolous embellishments of architecture often exhibit an elaborate symmetry or periodicity which are unrelated to function, as do the nonrepresentational patterns used to decorate articles such as carpets, pots, clothing, etc. This tendency towards symmetry and periodicity in art and architecture is common to all cultures throughout history, and therefore reveals a fundamental aspect of human nature. It might be argued that this preference for symmetry simply reflects a cognitive appreciation for order and regularity in the universe. Evidence from patterns seen in LSD hallucinations, [4] patterns inspired by ritual trance states and epileptic seizures [18] suggests however that even the lowest levels of the visual system have a tendency to generate symmetrical and periodic patterns as a natural characteristic of their functional architecture. What is the meaning and the purpose of the symmetry and periodicity in human perception?
Attneave [1] proposes that an answer to this question can be found in information theory [13]. He suggests that a fundamental property of visual representation is information compression, i.e. that the internal representation of a visual scene must be a compressed or abbreviated representation of that scene, in order to reduce to manageable proportions the overwhelming volume of information available at the retina. This idea is familiar in the field of image processing, where image compression techniques make use of redundancies in the image to generate a more compact representation. For example large uniform regions can be encoded by the transitions that occur at image edges, rather than as an explicit representation of image intensity throughout the region. The fact that line drawings are so meaningful to us suggests that such compression is a component of human perception. Similarly, straight or smoothly curving edges in an image can be compressed to a representation of their end points, by an assumption of the Gestalt principle of "good continuation". Attneave suggests that this kind of compression occurs in human perception, and presents as evidence "Attneave's cat", shown in Figure 5 (A), where the smoothly curving lines of a line drawing of a cat have been replaced by straight line segments without destroying the recognizability of the cat. This suggests that the information at the image vertices and line endings is sufficient for recognition. Indeed, Attneave suggests that all of the Gestalt principles are examples of regularity or redundancy in the visual world which are exploited by the visual system for information compression. Symmetry and periodicity are obvious candidates for compression, as they clearly represent redundant information. The question is, how is symmetry recognized by the visual system, and how is the compression performed? In the next section we will present the Orientational Harmonic model by Lehar [12], which proposes that symmetry is computed in the visual system by way of harmonic resonances in the visual cortex. We will first however address an issue that is intimately related to the notion of compression, and that is the idea of de-compression. If the visual system generates a compressed abstraction of the visual input, is it necessary for the visual system to posses a de-compression mechanism to convert that abstraction back into a brightness representation?
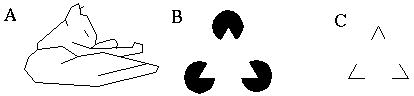
Attneave's cat, a line drawing where lines of low curvature are replaced by straight line seg- ments (A); Kanizsa triangle (B); triangular configuration without illusory triangle (C).
Consider the case of the Kanizsa triangle, shown in Figure 5 (B). In this figure an illusory triangle is generated from information available only at the vertices. The configuration shown in Figure 5 (C) contains the same evidence for the presence of a triangle, and produces a similar "high level" recognition of a triangular relationship, but in Figure 5 (B) there is something more- one can actually see the edges of the illusory triangle in a manner that is very similar to an actual brightness edge. The operation of "good continuation" in Figure 5 (B) therefore goes beyond a high level abstraction, and actually "paints in" the hypothesized edge with a high resolution brightness percept. Furthermore, these illusory edges even influence the perceptual brightness at the center of the triangle, where the paper appears to be a brighter shade of white than the paper outside the triangle. None of this information is present explicitly in the original image, but the visual system appears to find it necessary not only to extract the "high level" information about the triangular relationship, but also to perform a top-down completion of the lower level brightness representation on the basis of the high level abstraction. The phenomena of boundary completion and surface brightness filling-in are explained in the Boundary Contour System (BCS) and Feature Contour System (FCS) models respectively [5, 6, 7] which model these effects as a simultaneous bottom-up top-down relaxation in a multi-layer hierarchical visual representation.
A similar bottom-up / top-down interaction can be seen conceptually in embryonic morphogenesis shown in Figure 4 (A) and (B). The parameters of the reaction diffusion define the periodicity of the morphogenic pattern as a high level invariant representation of that pattern. The final pattern however is not a perfect geometrical embodiment of that periodicity, but rather an emergent compromise resulting from the interaction between the invariant high level pattern and the variable physical dimensions of the embryo, as if a "rubber template" representing the perfect canonical pattern were being stretched to accommodate the imperfect contingencies of the available physical substrate. This, we believe, is an important property of visual representation in biological vision.
Single cell recordings from the visual cortex of experimental animals have revealed the presence of oriented edge sensitive cells [8] which fire optimally in the presence of a visual edge of a particular orientation and at a particular location in the visual field. These findings have been incorporated into the Boundary Contour System (BCS) model, a portion of which is shown schematically in Figure 6. In this figure, the oriented edge sensitive cells, or "oriented cells", receive input from an image layer by way of oriented receptive fields in the manner of oriented edge detectors used in image processing, such that all orientations are represented at each spatial location.
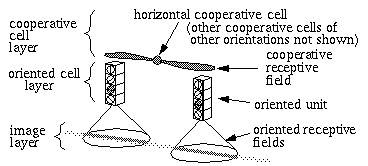
Structural architecture (simplified) of the Boundary Contour System model, showing cooperative cell which detects colinearity between oriented edges detected by oriented cells.
The principal function of the BCS model is to account for the phenomenon of colinear boundary completion as seen in visual illusions such as the Kanizsa triangle in Figure 5 (B). This is achieved by cooperative cells in a cooperative layer which receive input from the oriented layer by way of specialized receptive fields designed to detect colinearity. Colinearity is defined by oriented edge segments that are both parallel and spatially aligned. The horizontal cooperative cell depicted in the figure receives input exclusively from horizontal oriented cells in the oriented layer, which therefore satisfies the parallel requirement, and from receptive fields spatially aligned in the horizontal direction, which ensures that those inputs are also horizontally aligned. The cooperative cell will therefore only fire when it receives pairs of inputs which are in a colinear relation. The phenomenon of illusory boundary formation seen in the Kanizsa triangle is explained in this model by an activation of the cooperative cell that is interposed between the oriented inducers at the corners of the triangle, which in turn feeds activation back down to the oriented unit between the inducers (not shown in the figure) generating a weak activation in that unit as if in response to an actual oriented edge. The full BCS model is considerably more complex than this simple description, and in conjunction with the Feature Contour System (FCS) accounts for a wide range of diverse perceptual phenomena. What is significant to this discussion is that the colinearity response of this model is hard wired into the cooperative receptive field.
There are a number of illusory contours however which cannot be explained as a colinear grouping. For example, the Ehrenstein illusion, shown in Figure 7 (A) exhibits an illusory contour that forms orthogonal to the inducing lines. Also, the vertices of the illusory triangle shown in Figure 7(B) complete through an angle of 60 degrees. The BCS model can account for colinear grouping between a line of dots, as seen in the left-most portions of Figure 7 (C), but Kanizsa [10] has shown that the colinear grouping appears to break abruptly into sharp vertices when the curvature exceeds a critical value, as shown in the right hand portions of Figure 7 (C). This suggests that the mechanism responsible for illusory vertex completion is one and the same as the mechanism involved in colinear completion. Further evidence for a common architecture is seen in the four-line Ehrenstein figure shown in Figure 7 (D). Subjects report seeing this figure either an illusory circle, square, or diamond.
Ehrenstein illusion (A); illusory vertex completion through dots (B); illusory circles and illusory polygons (C); four-line Ehrenstein illusion (D).
Figure 8 shows that illusory vertices seen between patterns of dots can be defined by the intersection of one (A), two (B), three (C), or four (D) illusory boundaries which meet at each dot. Furthermore, an interesting distance dependent relationship is seen in the grouping patterns of these dots, where the pattern defined by the nearest neighboring dots determines the percept of the vertex, and masks the groupings defined by more remote dots. For example, in Figure 8 (B) the horizontal grouping is masked by the stronger vertical grouping because the vertical distances are smaller than the horizontal ones. If alternate rows of Figure 8 (B) were removed, the horizontal grouping would emerge, showing that the horizontally adjacent dots are sufficiently close to generate a horizontal grouping, but that grouping is masked by the nearer vertical grouping. Similarly, in Figure 8 (C) there are three nearest neighbors for each dot, which defines a three-way vertex passing through every dot in this pattern. If certain rows were removed from this figure, a strong vertical grouping would immediately appear. A similar effect is seen in the other patterns in Figure 8. A direct generalization of the BCS model to account for these phenomena would involve defining additional cooperative cells tuned to respond not only to colinearity, but also to "T", "V", "X" and "Y" vertices, among others. Just as in the case of the cooperative cell, each of these specialized hard wired receptive fields would have to be replicated at every orientation at every spatial location in the cortex. Furthermore, complex interactions would have to be defined between these vertex representations to account for the distance dependent relationship described above.

Illusory boundary formation through vertices composed of one (A), two (B), three (C), and four (D) oriented edges.
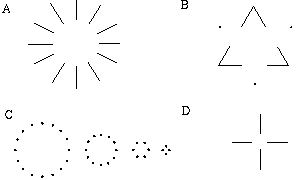
Neumann [16] proposes a more general architecture in the form of a "rosette" of receptive fields at every orientation, as shown in Figure 9, with a separate cell body receiving input from each of the oriented monopolar receptive fields. Lehar [12] shows that all of the perceptual phenomena described above, and many more, can be accounted for by a circular harmonic resonance within this ring of cells, which would promote a periodic pattern of neural activation within this ring of cells. The exact nature of the harmonic resonance responsible for these phenomena remains to be explored. The most likely mechanism is that the cells in the orientational rosette are connected by gap junctions, or electrical synapses, in a ring-shaped syncyctium . Kandell & Siegelbaum [9] observe that blocks of cells that are connected in such syncytia have been observed to fire synchronously. Allowing for a small propagation delay due to the inductance and capacitance of each cell, it would not be unreasonable to suppose that such syncytia would also be able to sustain harmonic oscillations of electrical activity. Since the resonances occur in a ring shaped structure, the action of the harmonics will be to subdivide the circumference of the cooperative rosette into integer numbers of equal intervals of alternating active and inactive regions. In an orientational representation, as in the rosette described above, the periodicity in the circular harmonic system represents an orientational periodicity, corresponding to a measure of symmetry, as shown in Figure 10. For example, a vertex consisting of four edges equally spaced in a "+" vertex would be represented by the fourth harmonic, because the edges subdivide the full circle into four equally spaced segments. A three way vertex with arms separated by 120 degrees would be represented by the third harmonic. A straight line through the vertex would be represented by the second harmonic, corresponding to the periodicity of two edges separated by 180 degrees. A vertex defined by a single orientation extending in one direction from the vertex represents the first harmonic oscillation. The zeroth coefficient corresponds to the DC term of a Fourier representation, i.e. a feature consisting of orientations in all directions simultaneously representing the overall magnitude of the oriented signal averaged over all orientations. A strong response to this coefficient alone corresponds to a small circular dot centered at the vertex, which would stimulate cells of all orientations simultaneously. As in a Fourier representation, other vertex combinations besides those represented by the first five harmonics of the Fourier series can be obtained by combinations of the harmonics. The exact mathematical formulation used in the computer simulations of the orientational harmonic system is described in the appendix.
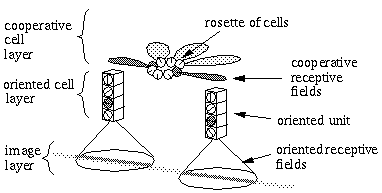
Structural architecture of Orientational Harmonic model showing "rosette" of monopolar cooperative cells which sustain circular harmonic resonances of neural activation.
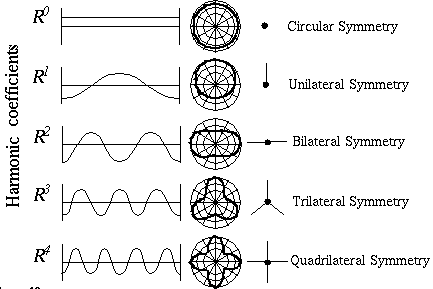
First five harmonics of circular harmonic series, and the various forms of symmetry that they represent.
The effect of orientational harmonics on visual perception is to promote and enhance periodicity in the orientational representation. For example, Figure 11 shows a visual input consisting of a single oriented input at six o'clock, indicated by the gray bar, together with plots of the first four harmonics of the orientational frequency, oriented as they would be in response to this single edge input, i.e. with one positive lobe of the periodic response centered at the six o'clock orientation. The first harmonic shows a positive response through the lower half circle (A), the second harmonic shows two peaks at six and twelve o'clock (B), the third harmonic shows three peaks at six, ten, and two o'clock (C), and the fourth harmonic shows four peaks at six, twelve, three and nine o'clock (D). A single edge input of this sort produces the strongest response in the first harmonic, and the higher harmonics would respond with progressively lesser magnitudes to this particular input. All of these harmonics would however be simultaneously present in the response to this input. A certain measure of `competition' and `cooperation' occurs between the patterns to be completed, although it occurs not by way of excitatory and inhibitory interactions between high level nodes in a neural representation, but rather by way of constructive and destructive interference between the waveforms in the orientational rosette. For example, the first harmonic end-stop response to the single edge input at six o'clock shown in Figure 11 (A) produces a negative peak at twelve o'clock, exactly where the second harmonic would produce a positive peak. These two harmonics therefore will tend to cancel one another at twelve o'clock by destructive interference. Similarly, the second harmonic response produces two negative peaks at three and nine o'clock, exactly where the fourth harmonic would produce positive peaks. The various harmonic responses to the single edge input represent the various potential completions that can be made from that input. Figure 11 (E) shows the locations of all the potential completion peaks of the first four harmonics in response to the single edge input.
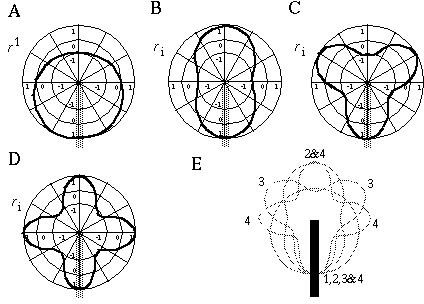
Response of the first (A), second (B), third (C), and fourth (D) orientational harmonics to an input edge at six o'clock; response of all four harmonics plotted together (E).
The actual pattern of illusory boundaries produced by an oriented edge would depend not only on the local orientational signal, but also on the influence of orientational signals from adjacent regions, which can "bring out" some of these potential completions while suppressing other competing patterns. For example given an edge at six o'clock, a nearby vertical edge in the twelve o'clock direction would promote the second harmonic response, resulting in a vertical grouping percept, as seen in Figure 12 (A). Figure 12 (B) and (C) show the input and output respectively of a computer simulation of this phenomenon. In this and the following simulations an orientational harmonic interaction was computed with a cooperative ring located at every pixel of the image. A dark color in these images represents a high level of cooperative activation summed through all of the orientations of the cooperative ring at that location. Notice that the darkest lines of cooperative activation correspond to the visible boundaries of the inducing lines, each inducing line in the input stimulating a double boundary in the cooperative layer corresponding to a light / dark edge on the left, and a dark / light edge on the right. The shaded lines between the inducers represent the location of the grouping lines. In Figure 12 (C) these lines define a predominant vertical grouping, as observed in the percept in Figure 12 (A). Notice also however the weaker horizontal and diagonal groupings in the same figure. In Figure 12 (D) a horizontal grouping predominates along the line endings. Orientational Harmonics would explain the horizontal grouping percept of Figure 12 (D) by a fourth harmonic grouping to adjacent line endings, which in turn suppresses the vertical second harmonic grouping. This phenomenon is reproduced in the computer simulation of Figure 12 (E) and (F), where a dark line of cooperative activation is seen to define an orthogonal end cut to the line endings due to the action of the fourth harmonic. Similarly the spatial arrangement shown in Figure 12 (G) promotes a diagonal grouping percept due to third harmonic grouping, which in turn suppresses the second and fourth harmonic responses. This effect is reproduced in the computer simulation shown in Figure 12 (H) and (I).
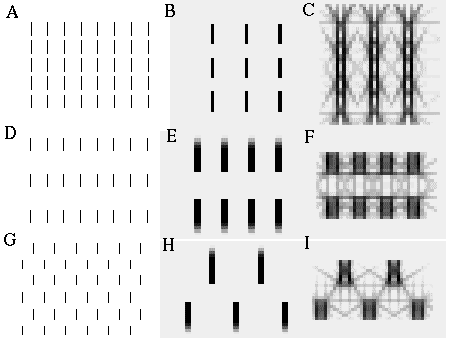
Vertical (A), horizontal (B), and diagonal (C) grouping of short line segments reproduced in computer simulations with inputs (B), (E), and (H) producing outputs (C), (F), and (I) respectively.
The situation is more complicated when the original feature at the vertex does not correspond to a simple orientational harmonic, but consists of a more complex form represented by a combination of the fundamental harmonics. For example, Figure 13 shows the response of the first four harmonics to an input consisting of a right angled corner, or "L" vertex. The first harmonic response in Figure 13 (A) produces a positive peak at the bisector of the internal angle between the two edges, because that orientation marks the center of the half-circle which contains the greatest oriented signal. The second harmonic shown in Figure 13 (B) produces absolutely no response to this pattern, since the two input features are separated by 90 degrees, which is exactly the angle between the positive and negative lobes of the second harmonic response, so that they cancel exactly. The third harmonic forms an optimal alignment with the two lobes aligned approximately with the two edges of the input figure, as shown in Figure 13 (C), leaving a third lobe to bisect the external angle between the two edges. Likewise, the fourth harmonic aligns with two lobes parallel to the two input edges, leaving two additional lobes as linear extensions to the input edges across the center of the vertex, as shown in Figure 13 (D). This analysis shows how the "L" vertex can be represented by a combination of the first, third, and fourth harmonics. The Orientational Harmonic model would therefore predict potential grouping lines for the "L" vertex in orthogonal and diagonal directions, as indicated in Figure 14 (E), although again, a strong diagonal grouping due to the third harmonic would tend to suppress the orthogonal grouping, and vice versa.
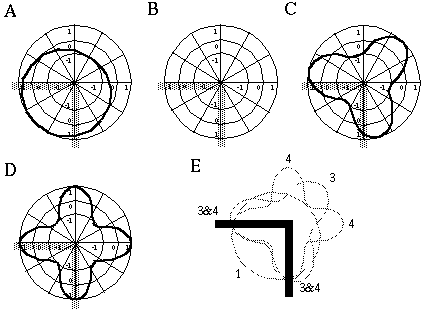
Response of the first (A), second (B), third (C), and fourth (D) orientational harmonics to a right angled input with edges at six and nine o'clock; response of all four harmonics plotted together (E).
Orientational harmonics therefore predicts that a square, which is composed of four such "L" vertices will posses similar orthogonal and diagonal potential grouping lines, as illustrated in Figure 14 (A), and that these two groupings will compete with each other, so that a strong percept of one would suppress the perception of the other. This suggests that squares will tend to group well orthogonally, as in Figure 14 (B), or diagonally, as in Figure 14 (C), but not both simultaneously. Figure 14 (D) and (E) show the input and output of a computer simulation showing the orthogonal grouping percept, while Figure 14 (F) and (G) show a computer simulation of the diagonal grouping effect. Notice that in Figure 14 (G) the actual grouping should occur at an angle of 45 degrees, which was not represented in the computer simulation due to orientational quantization, so the grouping percept is seen instead in the nearest represented orientations at 30 and 60 degrees.

Diagonal and orthogonal grouping lines from a square (A) suggest that squares will group in orthogonal (B) and diagonal (C) configurations; computer simulations of orthogonal (D) and (E), and diagonal (F) and (G) grouping of squares.
The most straightforward predictions made by the theory concern the illusory boundaries that form between patterns of dots, as shown in Figure 8. Each dot in the pattern stimulates oriented responses at all orientations uniformly, so that the formation of illusory boundaries is a result only of the geometrical configuration of the dots themselves, with no orientational bias introduced by the orientational signal at the dots. The model predicts, therefore, that isolated pairs of adjacent dots would tend to form a first harmonic completion, creating an illusory boundary joining those dots. This explains the pairwise grouping percept shown in Figure 8 (A). The first harmonic grouping suppresses the competing second harmonic grouping, which attenuates any completion beyond the two dots.
The Orientational Harmonic model also predicts a second harmonic grouping to result from a column of nearby dots, where each dot receives oriented inputs from neighboring dots at six and twelve o'clock. This explains the colinear grouping percept in Figure 8 (B), and is reproduced in the computer simulation in Figure 15 (A) and (B). The second harmonic in turn suppresses a fourth harmonic grouping at the same location, so that the Orientational Harmonic model predicts that a strong vertical grouping due to close vertical proximity should suppress a weaker horizontal grouping. If the vertical spacing is increased without changing the horizontal spacing, a horizontal grouping percept will emerge by disinhibition This is shown in the simulation of Figure 15 (C) and (D). If the horizontal and vertical spacings are the same, then the fourth harmonic will predominate, resulting in a four-way grouping percept, as seen in Figure 8 (D), reproduced in the computer simulation shown in Figure 15 (E) and (F).

Computer simulation showing vertical (A) and (B), horizontal (C) and (D), and simultaneous vertical and horizontal grouping of dots (E) and (F).
The Orientational Harmonic model explains the various alternate percepts seen in the four-line Ehrenstein figure shown in Figure 7 (D), which form an illusory circle, square, or diamond, as shown schematically in Figure 16 (A). A fourth harmonic grouping at the four line endings generates orthogonal end cuts to the inducing lines, which are then further completed either by second harmonic completion creating the illusory circle percept, or by fourth harmonic orthogonal completion creating the square percept. Alternatively, a third harmonic grouping at the line ending creates diagonal completion to the other line endings resulting in the diamond percept. The input and output of a computer simulation of these phenomena is shown in Figure 16 (B) and (C) respectively. The simulation result shows evidence of all three of the illusory figures reported by subjects. Careful examination is required to distinguish the circular grouping from the diagonal grouping in Figure 16 (C), but they do indeed diverge slightly, as suggested in Figure 16 (A). The simulation also exhibits a cross-shaped response through the center of the figure. This feature represents the amodal completion of the inducing lines behind the illusory foreground surface, which is invisible in the visual illusion, but not imperceptible, as one is aware of a colinear completion occurring invisibly behind an occluder. A full explanation of the distinction between a modal v.s. amodal percept, or visible v.s. invisible completion will require a three-dimensional extension to the orientational harmonic model, which would allow the illusory surface to be completed in front of the occluded cross.

Schematic depiction of the four-line Ehrenstein illusion showing the square, circle, and diamond illusory figures (A), and a computer simulation of the phenomenon (B) and (C).
By the principles of information theory, as discussed by Attneave [1], a primary function of the visual system is to encode visual information in a more compact representation for the purposes of recognition and recall. The orientational harmonic system described so far performs the inverse of abstraction, or reification, a filling-in or completion of a veridical facsimile or internal copy of the visual world. A higher level representation would have to extract significant features from this representation and to encode them in a compact form.
It so happens that the spatial pattern of acoustical harmonics in a resonant cavity is related to the temporal frequency, or tone produced by that harmonic. For example, the fourth spatial harmonic will have a temporal frequency that is double that of the second spatial harmonic, which in turn is double that of the first harmonic. In a linear tube, the spatial pattern is fixed in relation to that tube, but in a circular tube that spatial harmonic pattern can occur at any orientation. The temporal frequency on the other hand remains constant across different rotations of the spatial pattern, but is characteristic of the orientational frequency of that pattern. Temporal frequency therefore can be seen as a rotation invariant representation of the orientational harmonic pattern, and can be used both bottom-up, to identify orientational harmonics, or top-down, to prime or boost specific harmonics. A bank of sensors tuned to the temporal frequencies of the orientational harmonics therefore would detect the presence of their own harmonic in the input regardless of the absolute orientation. Furthermore, a bank of oscillators tuned to the same harmonic frequencies would stimulate periodic activity in the orientational harmonic system, and thereby establish a spatial pattern of standing waves representing one of the orientational harmonic vertex types. In this top-down priming of a vertex pattern, since the temporal frequency is rotation invariant, the vertex pattern would appear at some arbitrary orientation in the absence of bottom-up oriented input, or at an orientation that is most consistent with a weak or partial oriented input. We will show that this property of temporal frequency priming has significant implications for visual representation.
Neurophysiologically, both filters and oscillators could be implemented by neurons whose characteristic refractory period makes them tend to spike at a particular temporal frequency. Such cells would act as both filters and oscillators, since they would tend to fire more readily in the presence of electrical oscillations that match their characteristic frequency, and conversely, whenever they are active they will promote oscillations at their characteristic frequency, and thus stimulate standing waves in the orientational harmonic ring. Such cells need only be loosely coupled to an orientational harmonic ring in order to influence it, and be influenced by it, just as an extracellular electrode can be used for both recording and stimulating neural activity in nearby regions of neural tissue. We propose therefore that there are such temporally tuned cells in the vicinity of the orientational harmonic ring which are tuned to the fundamental harmonic frequencies of that ring, and whose activation either records or stimulates those waveforms in the ring.
The next computer simulations illustrates these principles. In these simulations the harmonics of the system are investigated at a single location in the system, as represented in Figures 11 and 13. Figure 17 (A) shows the results of these simulations. The thick radial lines extending outwards from the inner circle plots the input pattern of oriented cell activation, while the shaded region plots the equilibrium activation of the cooperative cells quantized into twelve orientations, as indicated by the thin radial lines. The bar charts to the right of the dials depict the harmonic content of the bottom-up input. This response represents the bank of tuned filters that detect the temporal oscillations corresponding to the orientational harmonics. Additional bars displayed to the right represent the top-down prime, corresponding to the tuned oscillators that can stimulate particular harmonics in the system. As discussed above, the filters and oscillators could actually be embodied in the same mechanism, although they are kept separate in these simulations to distinguish a bottom-up and top-down flow of information.
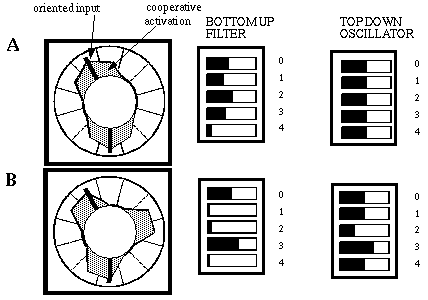
Harmonic response to an ambiguous vertex feature with no priming (A), and the effects of priming for the third harmonic with the same input pattern (B) showing the spontaneous appearence of a third branch of cooperative activation.
Figure 17 (A) shows the response of the system to an ambiguous input pattern, chosen to stimulate both the second and third harmonic responses, although the second harmonic records a somewhat closer match to this pattern, as seen by the somewhat stronger response of the second harmonic filter. This pattern of harmonic response is invariant to the rotation of the input pattern. The top-down prime was then progressively adjusted by increasing the third harmonic oscillator while reducing the fourth harmonic oscillator until the configuration of primes depicted In Figure 17 (B) was achieved. All the while, virtually no change was observed in the pattern of activation in the cooperative ring except a slight reduction in cooperative cell activity at the twelve and five o'clock orientations, together with a slight increase in activity at the ten and seven o'clock positions. A critical transition was seen to occur at the configuration of top-down priming values shown in Figure 17 (B), when suddenly a bud of activation was seen to appear at the two and three o'clock positions, followed by a rapid reconfiguration of the activation patterns in the cooperative representation, accompanied by an abrupt change in the bottom-up harmonic representations. The equilibrium values for the cooperative pattern and the harmonic response are shown in Figure 17 (B).
This model raises several interesting issues of relevance to visual perception and representation. In many visual models, features are extracted from the input by specialized feature detectors, the response to each feature being represented by the activation of the corresponding node. In models that involve competition or cooperation between features, that interaction is often implemented by lateral inhibition or excitation between these higher level nodes. The system proposed here is fundamentally different in the sense that what competition or cooperation exists in the model, occurs not by way of explicit interactions between high level representations, but rather occurs node by node at the lower level of representation by way of constructive and destructive interference between competing waveforms in a distributed representation. Indeed, that interaction between competing representations occurs independent of the higher level representation, and can be seen as a low level consistency matching at the highest possible resolution in the system between alternative representations of the input signal.
The manner in which the top-down priming influences perception in the system is also noteworthy. In the simulation depicted in Figure 17 (A) and (B), the ambiguous input pattern stimulated both the second and the third orientational harmonics, leading to a response in the second and third harmonic filters. During the dynamic simulation shown in (B), when the top-down bias favoring the third harmonic is first applied, the interactions between waveforms in the cooperative representation slowly bends the activations of the two branches of the bilateral pattern against their natural tendency to remain colinear, in an attempt to make room for a third branch, even though the bottom-up second harmonic filter response still dominates the third harmonic response. A sudden change is seen to occur as soon as an illusory third branch sprouts, after which the system quickly re-equilibrates to a third harmonic condition as the third branch grows in size and the bottom-up feature representation reflects a predominantly third harmonic pattern.
In this system therefore, the priming of the third harmonic oscillator initiates a fundamental shift in the balance of forces at the lower level cooperative representation, causing the pattern there to bend as if under stress, as the third harmonic attempts to establish a third branch of activation. The success of this priming on changing the final percept depends intimately on the context at the lower level, whether the rest of the inputs at that location, and at neighboring locations in a full simulation, are also consistent with this new trilateral pattern. In a full simulation complete with neighboring units and oriented input, the bending of the two arms of the bilateral pattern would subtly shift the forces in all the neighboring cooperative units, resulting in a different dynamic balance of forces throughout the cooperative layer. This new balance of forces could either promote the growth of the third branch (by increasing the activation at the two and three o'clock orientations), or inhibit it, in a way that would be impossible to predict by analysis of the high level representation alone. The manner of operation of the top down priming in this system therefore is not in the form of an "intellectual" competition between the high level abstractions represented by the second and third harmonic oscillators, but rather, the competition is more of a "physical" struggle between the low level embodiments of these high level nodes, in the context of the lattice of interacting forces in the cooperative layer. The top level nodes communicate the urgency, and monitor the outcome of the competition between representations, but the competition itself takes place at the lowest level between the waveforms themselves.
The orientational harmonic model was devised to account for a number of perceptual phenomena observed in visual illusions. This model has deep implications for the nature of visual processing and representation in biological vision. It clarifies the relationship between a lower level variant explicit representation and a high level invariant compressed representation. Contrary to assumptions behind many other models of vision, this model suggests that visual processing is not a simple feed-forward process, where each stage performs some form of transformation which is simply passed upward to higher levels, but rather that the low and high level representations are complimentary, each one representing what the other cannot, and that a close dynamic coupling between lower and higher level representations is essential to maintain consistency throughout the visual hierarchy. This principle will be exemplified with a thought experiment.
We have discussed how the temporal frequency of oscillation reflects a rotation invariant representation of the low level input expressed in terms of the orientational symmetries of that pattern. In other words a single temporal frequency in the orientational harmonic system represents all the possible orientations of the corresponding orientational frequency pattern in a many-to-one manner. Since it is expressed in terms of angles, the orientational representation is fundamentally invariant to changes in scale. Furthermore, replication of the harmonic mechanism in a spatial array of orientational units could also add position invariance, as long as a single set of global tuned filters could receive input from any unit in the array. This mechanism therefore represents a rotation, translation and scale invariant representation of visual form, as will become clear in the example shown in Figure 18.
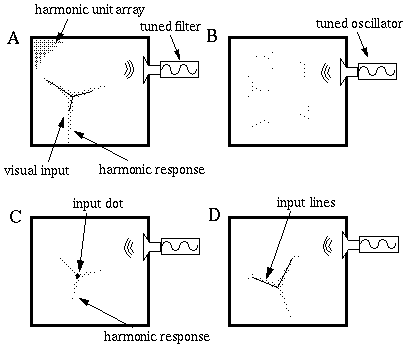
Many-to-one invariant recognition (A) and one-to-many top-down priming (B) which can per- form figural completion specific to the partial input provided (C) and (D).
If a third harmonic pattern, i.e. a three-way vertex were presented to a two dimensional matrix of orientational harmonic units, the system would produce a characteristic third harmonic tone in temporal frequency, regardless of the location, the rotation, or the scale of the pattern, as suggested in Figure 18 (A), where a visual input in the form of a triangular star, depicted by the black lines, stimulates a third harmonic pattern of activation represented by the shaded region, which tends to extend and regularize the input pattern, while generating a characteristic third harmonic tone. The tone remains constant through any rotations, translations, or scaling of the input pattern. This represents a many-to-one transformation from an infinite variety of instances to a single invariant feature, which can be detected by an acoustic filter tuned to that frequency
In the top-down mode, the filter can be replaced by a tuned oscillator that transmits the third harmonic acoustic frequency and broadcasts it to all the harmonic units in the array. Each unit in the array would attempt to "hallucinate" a triangular vertex, but the overlapping and intersecting signals would cancel each other out, resulting in an approximately uniform pattern of activation, as suggested in Figure 18 (B). A visual input applied during such priming would break the symmetry of this mutual inhibition, and triangular stars would begin to appear. Given an input in the form of a single dot, for example, this input would favor triangular stars of all orientations equally at that location, so that with sufficient top- down priming the system would hallucinate the primed feature centered at the dot, at some arbitrary orientation, as shown in Figure 18 (C). In this case only the location of the primed pattern is constrained by the input, so that the other degrees of freedom remain arbitrary. If the input supplied is more specific, then the resultant pattern will be further constrained, as shown in Figure 18 (D), where the input consists of two oriented edges that meet at a vertex. The minimum energy configuration for this input is to have two arms of the three pointed star coincide with these lines, leaving the third to bisect the external angle with an illusory boundary. Note the weaker third harmonic responses generated by the line endings.
An important organizational principle is seen in this example. The higher level invariant representation does not encode a single canonical exemplar of the encoded pattern, but rather it simultaneously encodes all possible instances, as can be seen in the case of top-down priming of that feature. Given sufficient top-down priming such a system would be able to "hallucinate" a single exemplar selected at random from the multiple possible instances even in the absence of any input, and that emerging pattern would in turn would suppress all other competing instances of that pattern. The more usual mode of operation however is to provide equal priming to all harmonics, and only enough priming to allow the pattern to emerge on condition that it resonates with corroborative evidence from the bottom-up input. The greater the bottom-up evidence for the pattern, the greater the high level response and therefore the more aggressively the system fills-in and completes the missing features of the pattern. Notice however that although the top-down representation is invariant to rotation and translation, the pattern completion is specific to the variant lower level input. The top-down priming therefore is a one-to- many, or more accurately a one-to-one-of-many relationship with the emerging lower level pattern. The actual pattern "perceived" by this system is not represented exclusively in either the higher or the lower levels, but rather is present at both levels simultaneously, and each level encodes only those aspects of the pattern which are appropriate to that level. The lower level "perceives" a number of edges at specific translations and rotations, but is "unaware" of the global relationships between those edges, whereas the high level encodes the global configuration, but has no "knowledge" of the specific translation or rotation of that invariant pattern.
The nature of this invariant top-down priming can be demonstrated in the case of the four-line Ehrenstein figure, which rests on a saddle point in perceptual space, and can be seen in three alternative ways. Coren et al. [3] report that top-down priming can influence the probability of perceiving this figure as one or another of the several possible forms. Figure 19 shows a repeat of the computer simulation of the four-line Ehrenstein illusion shown in Figure 16 except that in this case a top-down priming signal was applied for the second, third, and fourth harmonics in Figure 19 (A), (B), and (C) respectively. The priming in this simulation is applied uniformly to the entire image, non-specific to either spatial location, nor to orientation. The effects of the priming however have very specific spatial and orientational results, depending on the context in the image. Those features that are consistent with the primed harmonic will respond to the prime at the location of that feature and at the specific orientation where that harmonic fits best. In Figure 19 (A) for example the second harmonic priming emphasizes the colinearity of the illusory boundary, producing the circular Ehrenstein figure. This response should be compared to the un-primed response illustrated in Figure 16 (C). Note that in this simulation, the "circle" in the middle is actually a dodecahedron, because of the quantization in the simulation to twelve orientations. Figure 19 (B) shows the result of priming with the third harmonic. It is this harmonic that is responsible for the diagonal lines extending from the corners of rectangular features, so this orientational frequency will stimulate a percept of the diamond shape in the four-line Ehrenstein figure. Figure 19 (C) shows the Orientational Harmonic response with a priming of the fourth harmonic, which boosts the right angle vertices of the figure, resulting in strong corner responses to the square perceptual figure, as well as bringing out orthogonal intersections throughout the image. The simulation results shown in Figure 19 were normalized to the maximal activation in order to bring out the weaker responses, which explains why the non-illusory boundaries of the inducers appear much stronger in Figure 19 (B), where more boosting was required than in Figure 19 (A) and (C).

Top-down priming of the four line Ehrenstein illusion showing the emergence of the circular (A), diamond (B), and square (C) illusory figures when primed with the second, third, and fourth harmonics respectively.
The orientational harmonic model makes an interesting statement about the meaning of symmetry in visual perception. On the one hand, symmetry represents a redundancy in the visual representation which offers an opportunity for information compression, as suggested by Attneave [1]. There is however another very important principle revealed by this model, which has to do with the top-down interaction between the higher and lower levels of representation. The lower levels of the visual hierarchy are often considered as simply pre-processing stages, which perform some kind of elementary computations on the visual input, and pass the result on to higher levels where the significant processing occurs. Taken to its logical conclusion, this approach leads to the "Cartesian theatre" idea of consciousness, whereby the highest level brain center integrates the pre-processed symbolic interpretation from the various sensory modalities at a single central location. It is supposedly at this central location that cognition occurs, including logical thought, decision making, and consciousness. The concept is somewhat like the "black board" model used in artificial intelligence programs to serve as a central clearing house where symbolic information from multiple modalities can be checked against each other for global consistency.
The orientational harmonic model suggests a far more important and significant role for the lowest levels of the visual system. Far from being simply a pre-processing stage, the low levels act as a sounding board to express the higher level abstractions in a high resolution concrete representation. Consider the example shown in Figure 18 (D), where a right angled feature is presented to the lowest level of the system. The third harmonic oscillator represents a high level "hypothesis" about the meaning of that input, but application of that hypothesis to that low level input has low level implications in the form of the illusory third branch which emerges when that hypothesis is active. Whether those implications are consistent with the rest of the image can only be determined at the lowest level, where that illusory branch will find either confirmation or dis-confirmation from adjacent features in the image. If confirmation is found, for example by the presence of another line segment colinear with the illusory third branch, the entire third harmonic pattern will gain strength, which in turn will enhance the response of the high level third harmonic hypothesis. The hypothesis by itself is as meaningless as the firing of an isolated neuron surgically removed from the rest of the brain. It is only by its influence on the lowest level of representation that the high level node has any real meaning at all.
This approach to visual perception gives a new meaning to the role of symmetry in perception. There is little purpose served by simply detecting and measuring a regularity or symmetry in an input pattern. The real purpose of symmetry is to use that regularity to make predictions about unseen portions of the image. It is the very regularity in a symmetrical pattern which allows it to be used to make such predictions. Harmonic resonances in the brain therefore are an expression of an assumption that underlies all of perception, which is that in the absence of contradictory evidence it will be assumed that the visible portion of the visual input is a representative sample of the visual world, the whole of which can be reconstructed by simply replicating the visible portion in a symmetrical manner. This symmetrical replication is seen in the orientational harmonic response to a feature such as an isolated visual edge, where each harmonic interprets that edge as an incomplete exemplar of its own canonical pattern, as shown in Figure 11 (E), and attempts to perform figural completion based on that assumption. All such hypotheses are advanced simultaneously and in parallel, and result in a balanced state of mutual cancellation unless bottom-up evidence supports one hypothesis over the others. A "symmetry engine" of this sort, when over activated, can run amok, generating multiple symmetries simultaneously in a rich kaleidoscopic matrix, as is seen in the intricate network and filigree patterns observed in LSD hallucinations, and embodied in the elaborate decorative patterns which have adorned human artifacts since the earliest days of man. A hierarchical visual representation with this same tendency towards symmetry will hallucinate compound patterns of hierarchical symmetry, as seen for example in the great cathedrals of Europe, which exhibit a single global symmetry composed of smaller symmetrical components which themselves are composed of multiple local symmetries in a fractal self-similar manner. The invariance of the harmonic representation explains how a single geometrical signal representing a particular type of symmetry can be interpreted simultaneously by the multiple components in a compound geometrical shape, each one applying that invariant symmetry in its own rotation translation and scale variant manner.
The utility of the assumption of symmetry in practical perception is that it creates a percept of the whole when only a part is exposed. This occurs at all levels of perception simultaneously. At the lowest levels it is manifested in the completion of simple geometrical forms behind occluders, as in the Kanizsa triangle and the Ehrenstein illusion. At higher levels it completes more complex compound symmetries, such as a partially occluded face, or in three dimensions, completing the hidden back side of a quasi- symmetrical object like a house or a car. At the most global level the symmetry assumption creates a single coherent percept of the world about the egocentric axis, allowing for example a single local view of the horizon to generate the percept of a complete surrounding horizon, or a view of one corner of a room to complete the percept of the whole room surrounding the body in all directions. In the absence of contradictory evidence this assumption of symmetry provides a working hypothesis of the geometry of surrounding space at the highest possible resolution, which is essential for practical interaction with the environment.
[1] Attneave, F. (1954). Some Informational Aspects Of Visual Perception. Psychological Review, 61, 183-193.
[2] Chladni, Ernst F. E. (1809) Traite d'Acoustique.
[3] Coren, S., Porac C., & Theodor L. H. (1986). The Effects of Perceptual Set on the Shape and Apparant Depth of Subjective Contours. Perception and Psychophysics, 39, (5), 327-333.
[4] Ermentrout G. B., & Cowan J. D. (1979) A Mathematical Theory of Visual Hallucination Patterns. Biol. Cybernetics, 34, 137-150.
[5] Grossberg, Stephen, & Mingolla, Ennio (1985). Neural Dynamics of Form Perception: Boundary Completion, Illusory Figures, and Neon Color Spreading. Psychological Review, 92, 173-211.
[6] Grossberg, Stephen, & Mingolla, Ennio (1987). Neural Dynamics of Surface Perception: Boundary Webs, Illuminants, and Shape-from-Shading.. Computer Vision, Graphics and Image Processing, 37, 116-165.
[7] Grossberg, Stephen, & Todorovic, Dejan (1988). Neural Dynamics of 1-D and 2-D Brightness Perception: A Unified Model of Classical and Recent Phenomena. Perception and Psychophysics, 43, 241-277.
[8] Hubel, D. H. & Wiesel, T. N. (1959) Receptive Fields and Functional Architecture of Monkey Striate Cortex. J. Physiol. 148, 574-591
[9] Kandell, Eric R., & Siegelbaum, Steven (1985) Principles Underlying Electrical and Chemical Synaptic Transmission. In Principles of Neural Science, Kandell, Eric R., & Schwartz James H. (Eds.) Elsevier Science Publishing Co., New York.
[10] Kanizsa, Gaetano (1987). Quasi-Perceptual Margins in Homogeneously Stimulated Fields.. In The Perception of Illusory Contours, Petry S. & Meyer, G. E. (eds) Springer Verlag, New York, 40-49.
[11] Kauffman S. A., Shymko R. M., & Trabert K. (1978) Control of Sequential Compartment Formation in Drosophila. Science 199, 259-269.
[12] Lehar S. (1994) Directed Diffusion and Orientational Harmonics: Neural Network Models of Long- Range Boundary Completion through Short-Range Interactions. Ph.D. Thesis, Boston University.
[13] Miller, G. A. (1953) What Is Information Measurement? American Psychologist, 8, 3-11.
[14] Murray J. D. (1977) Lectures on Non-Linear Differential Equation Models in Biology. Oxford, Clarendon Press.
[15] Murray J. D. (1981) A Pre-Pattern Formation Mechanism for Animal Coat Markings. J. Theor. Biol. 88, 161-199.
[16] Neumann, H. & Stiehl, H. S. (1991) Modellierung von Mechanismen der Praattentiven Formenwahrnehmung fur Statische Achromatische Bilder. Proc. 36. Internationales Wissenschaftliches Kolloquium, Vortragsreihe A3 "Neuronale Netze", 643-648.
[17] Newman S. A., & Frisch H. L. (1979) Dynamics of Skeletal Pattern Formation in Developing Chick Limb. Science, 205, 662-668
[18] Siegel, R. (1976) Hallucinations. in The Mind's Eye, Readings from Scientific American, W. H. Freeman & Co., New York, 109-116.
[19] Turing A. M. (1952) The Chemical Basis of Morphogenesis. Philos. Trans. R. Soc. London, 237 B, 37-72
[20] Welsh B. J., Gomatam J., & Burgess A. E. (1983) Three Dimensional Chemical Waves in the Belousov-Zhabotinskii Reaction. Nature, 304, 611-614
[21] Wolpert, L. & Hornbruch A. (1987) Positional Signalling and the Development of the Humerus in the Chick Limb Bud.. Development, 100, 333-338.