Ph. D. Thesis
Boston University 1994
Attneave [1] discusses the relevance of information theory [41] to the issue of representation in the visual system. According to the tenet of information theory, information compression is an essential component to visual abstraction. This work reveals a duality in the nature of visual processing, which can be separated into two complementary functions, that of a bottom-up abstraction, and of top-down completion of visual information. These complementary functions will be discussed in the following sections, together with a discussion of the Boundary Contour System / Feature Contour System models (BCS / FCS) vision models [18, 19, 21] where the operations of boundary completion and brightness filling-in are examples of the latter function of visual processing. In the following chapters I will present two models that inherit many properties of the BCS model. The first model is a directed diffusion to allow boundary completion to occur across gaps that are larger than the size of the filter responsible for the completion. The second model is a theory that invokes harmonic oscillations in the oriented representation of the model in order to account for boundary completion through image vertices defined by multiple orientations at a single location. This model makes specific predictions about a wide range of visual illusions. Finally, a model of abstraction and representation of visual information, is presented as an extension to the orientational harmonic theory. This model will be shown to have properties of bottom-up top- down resonant matching as seen in the Adaptive Resonance Theory (ART) [5]
The phenomenon of illusory boundaries offers an invaluable tool for probing the mechanisms of visual perception because the illusory nature of these manifestations reveals their origin as being exclusively from within the visual system, rather than due to actual features present in the input. In other words, illusory phenomena factor out the perceptual mechanism from the object of perception. The study of these illusions therefore allows a precise characterization of internal interactions within the visual system. A large body of research has emerged over the last decades with the objective of quantifying precisely the conditions under which illusory phenomena occur, the types of illusions that occur under those conditions, and the exact nature and salience of the resulting illusions.
As a result of these studies, it has become apparent that the mechanism responsible for illusory phenomena exhibits lawful interactions between inducing features, and these interactions can be characterized by general principles that apply in a large number of individual cases. The first serious attempt to codify these laws was made by the Gestalt psychologists [67, 68, 40]. These researchers proposed a list of general and often abstract properties that are seen in the illusory phenomena. The Gestalt grouping laws suggest that similarity, proximity, good continuation, symmetry, good gestalt, common fate, etc. are properties of visual stimuli that tend to support global grouping percepts. While these laws are meaningful in a qualitative sense, they are difficult to quantify with sufficient precision as to make reliable predictions about illusory phenomena. As a result, it was difficult to propose specific mechanisms of visual perception based on these general, empirical laws.
Certain significant observations about the nature of visual perception were however revealed by the Gestalt laws. Chief among these was the concept that visual perception is not a simple feed-forward system amenable to reductionist analysis, because the perception of basic elements or visual primitives appears to be strongly influenced by global groupings of those elements. This poses somewhat of a chicken-and-egg paradox, because the global groupings themselves are defined by the visual primitives of which they are composed. The Gestalt insight therefore was that visual elements interact with one another by way of field-like influences, reminiscent of electrical or magnetic fields, whereby every element is influenced simultaneously by every other element, and global groupings emerge as a result of the simultaneous interactions between local elements, even as local elements emerge under the influence of the global groupings that they engender. Gestalt modelers exemplified this concept by way of physical analogies, such as the soap bubble, whereby a global symmetry is seen to emerge by way of purely local interactions between individual elements in the soap membrane; or the wooden spline, which assumes the shape of a globally smooth curve between clamped endpoints by way of local elastic interactions.
The recent emergence of neural network models has provided a more quantitative paradigm for expression of the field-like interactions proposed by the Gestalt models. Neural network models make use of neural receptive or projective fields defined by smooth spatial functions to mediate the spatial interactions between individual units representing specific visual features. The simultaneous emergence of local features and global groupings can be modeled by way of a parallel analog relaxation in a dynamic neural network model, implemented in computer simulations by iterative calculation of both bottom-up and top-down interactions; the bottom-up to represent the influence of the visual element on the global grouping, and the top-down to represent the influence of the global grouping on the perception of the elements. Neural network models are also consistent with neurophysiology, forming a bridge between theories of mind and brain. On the one hand the visual system detects visual features and represents them in an abstract, compressed form for recognition and recall, while on the other hand it maintains a veridical facsimile of the external visual world in a form available for internal use.
Attneave has formalized the Gestalt notion of field-like interactions within the context of information theory. Specifically, he points out that visual perception involves the two separate and complementary functions of abstraction and completion. Abstraction involves the elimination of redundant information, in order to reduce to manageable proportions the overwhelming volume of data available at the retina. For example, Attneave [1] shows how image information can be encoded more compactly as a function of the transitions which occur at image edges, rather than as an explicit representation of image intensity. This principle is well known in the field of image processing, where image compression techniques convert images to representations with a minimum of redundancy. A fundamental principle behind such techniques relies on the observation that regions of uniform or repeated values can be encoded as a single value for the whole region, together with the boundaries of the region over which that value holds. Since the dimensionality of the boundaries is always less than that of the region they delimit, a considerable savings of storage resource can often be realized. The encoded information itself may contain redundancy which can be further reduced by higher levels of encoding. For example, in the case of an image containing uniform regions, if the boundaries of those regions consist of regular forms such as lines or arc segments, a further reduction can be achieved by encoding the regularity or pattern of those forms, together with the bounds between which they apply. This process can be repeated any number of times as long as there remains some regularity or redundancy in the representation. The result is a compact, hierarchical description of the original data in terms of patterns of regularity found at each level.
The notion that this kind of compression occurs also in natural vision is supported by neurophysiological studies of the retina which indicate that even at this earliest stage of visual processing, the information available at the photoreceptors is transformed by retinal processing into spatial and temporal derivatives of the input. Adelson and Bergen [38] discuss how a spatial derivative of the local average of intensity in two dimensions is similar to the on-center off-surround response of the retinal ganglion cell, and that the derivative taken in one dimension is equivalent to an oriented edge representation, as in the simple cell response of the visual cortex. Within this type of system, a long straight edge would produce a repeated or redundant pattern of response, allowing for a possible compression of such edge information. For example, the edge could be encoded by a representation of the derivative of the orientation, i.e. the curvature. Points of high curvature therefore could be used to represent the bounds of intervening lines of low curvature without loss of information.
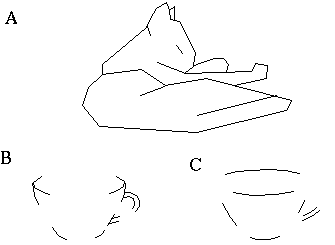
Attneave [1] illustrates how the points of highest curvature in a line drawing are sufficient to communicate the subject of the drawing. He presents as evidence "Attneave's Cat", shown in Figure 1 (A). This is a line drawing in which the lines of low curvature are replaced by straight lines, while preserving the recognizability of the cat. Similar evidence is presented by Biedermann, [4] who shows that removal of the low curvature lines from a line drawing preserves its recognizability as shown in Figure 1 (B), while removal of the points of high curvature makes the drawing unrecognizable, as showin in Figure 1 (C). These examples suggest that the points of high curvature may be sufficient to uniquely characterize a figure for human perception, and that the low curvature connecting lines can be reconstructed from the information found at the points of high curvature. In this sense, therefore, the lines of low curvature can be considered redundant information.

Attneave's cat (A); a sketch where the low curvature connecting lines have been replaced by straight lines, preserving only the points of high curvature, or vertices. Biederman's cup showing removal of lines of low curvature (B), or high curvature (C).
Further support for this notion comes from visual illusions such as the Kanizsa figures, as shown in Figure 2 In these figures, short oriented line segments, or inducers, are seen to generate illusory boundaries when the inducers are sufficiently aligned to be connected by low curvature lines. Perception of the illusory line drops off as a function of difference in orientation or displacement between the inducers. These illusions clearly illustrate that the visual system is capable of connecting high (and low) curvature points with low curvature illusory boundaries.
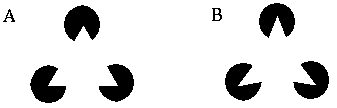
Kanizsa triangle (A) and curved Kanizsa triangle (B) showing the formation of an illusory triangle between inducers.
It is unlikely that this property of the visual system serves only to create visual illusions. A more likely conclusion is that the illusory boundary phenomenon reveals a fundamental mechanism of vision, which serves to complete boundaries that are broken or incomplete, active in real figures as well as illusory figures. If the low curvature boundaries of these illusory figures are represented implicitly by the boundary completion process, then explicit representation of those same boundaries would constitute redundant information. According to information theory, as discussed by Attneave, the visual system would most economically encode visual forms by encoding only vertices and points of high curvature, leaving the intervening edges to be encoded implicitly by the boundary completion process. Indeed, studies of saccadic eye movements such as those by Yarbus in 1957 (described in Hubel [25]) lend further support to this notion by revealing that visual saccades tend to jump between points of high curvature, with little time devoted to the areas in between. This indicates that these high curvature points contain information important for recognition. This raises an important issue on the subject of detection in vision models. Can it be said that a low curvature boundary has been "detected" by the visual system unless its presence has activated a specific cell tuned to that feature, which would remain inactive in the absence of that feature?
Zucker [71], Koenderink [34], and Parent [49] discuss the issue of curve detection in natural vision from a different perspective. In their view, curves represent specific features to be detected by specific curvature detectors. Zucker derives a mathematical form for curve detectors using considerations of cocircularity between oriented edges, to detect low curvature boundaries. In other words, Zucker proposes specific feature detectors for features which are redundant for recognition. A principal problem with this approach is that of combinatorial explosion. If curves are to be detected as explicit features rather than implicit completions, the visual cortex must posses specific detectors for every curvature at every orientation at every spatial location represented in the system. While the number of such detectors required may not be inconsistent with the known physiology of the visual cortex, this kind of combinatorial branching, especially when extended to higher level features beyond curvature, works contrary to the principles of information theory, geometrically increasing rather than decreasing the number of explicit representations of the visual stimulus at higher levels of the representational hierarchy.
The Boundary Contour System (BCS) [18, 19, 21] presents an alternative approach to curve detection that is more consistent with the concepts of information theory. Together with the Feature Contour System (FCS) [18, 19, 21] this model accounts for a wide range of psychophysical phenomena including visual illusions such as the Kanizsa figures. These two models in combination suggest that visual perception involves two distinct but interacting mechanisms, a boundary system which represents image edges and the interactions between them, and a feature system which mediates surface and brightness perception between boundaries represented in the BCS system. It is the grouping properties of the BCS that are responsible for the illusory boundary phenomena seen in the Kanisza figures, and the BCS will therefore represent the principal focus of this study. Figure 3 illustrates the basic architecture of the BCS. The cells at Figure 3(A) represent a layer of light sensitive cells such as the ganglion cells from the retina. The cells at Figure 3(B) represent cortical simple cells that receive input from the ganglion cells through oriented receptive fields, so that different cells at Figure 3(B) respond to edges of different orientations at Figure 3(A). For example the horizontal dark/light cell at Figure 3(B), highlighted in the figure, receives input from the highlighted elliptical region in layer (A), excitatory from the light half and inhibitory from the shaded half. All of the cells depicted at Figure 3(B) receive input from the same spatial location at Figure 3(A) through overlapping receptive fields at different orientations. The cells in layer (C) receive input from pairs of cells in layer (B) which represent edges that are parallel in orientation but of opposite direction of contrast. For example the highlighted cell at Figure 3(C) receives input from the horizontal dark/ light and the horizontal light/dark cells at Figure 3(B), producing an oriented representation that is independent of direction of contrast. The three big blocks at each layer represent three horizontally adjacent locations in the visual field.
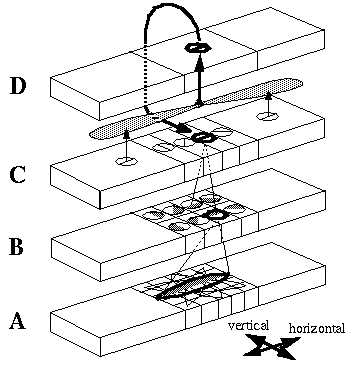
Boundary Contour System (BCS) architectural overview. An image layer (A) consists of photodetectors which provide input to a set of contrast sensitive oriented edge detectors (B) in the next level by way of oriented receptive fields. A higher level oriented representation (C) receives input from pairs of cells of opposite direction of contrast in the previous layer resulting in a contrast insensitive response. Finally, a cooperative layer (D) receives input from contrast insensitive oriented cells at adjacent locations in order to respond to extended edges that pass through the central location. A feedback loop performs boundary completion at the central location when the appropriate inputs are found at adjacent locations.
A principal feature of the BCS model is its ability to perform boundary completion between oriented edges that are approximately aligned, like the inducers of the Kanizsa figures which produce illusory boundaries. The mechanism responsible for this boundary completion is a layer of cooperative cells depicted in Figure 3(D) which receives input from layer (C) through large, bipolar oriented receptive fields. Like the receptive fields of layer (B), these bipolar receptive fields occur at every orientation at each spatial location, but unlike those fields the cooperative cell receptive field spans many spatial locations (although only two are shown in the figure) in a direction parallel to the orientation of the inputs preferred by the cooperative cell. For example, the horizontal cooperative cell depicted in the figure has a receptive field that is horizontally aligned to receive input from layer (C) horizontal cells at horizontally adjacent locations.
Parametric studies by Kellman and Shipley [31] show that illusory boundaries can form even when the inducers are not perfectly aligned, although the salience of the boundaries drops off smoothly with increasing misalignment. The BCS model accounts for completion between such misaligned inducers by incorporating a certain spatial and orientational uncertainty in the receptive field of each bipole, that is, each bipole receives somewhat attenuated input from inducers that are nearly but not perfectly aligned in spatial location, spatial orientation, or orientation of the input inducer. It is this spatial and orientational uncertainty in the receptive field that allows the BCS to perform boundary completion across curved boundaries, such as that shown in Figure 2 (B).
Grossberg and Mingolla [18] observe that the boundary completion process occurs only inwards between inducers, never outward beyond inducers. This feature is implemented in the model by a conjunctive requirement between the two lobes of the filter, which specifies that the cooperative cell will not fire unless it receives input from both lobes simultaneously. Neurophysiological measurements from single cells in the visual cortex by von Der Heydt et al. [63] confirm the existence of cells with such properties. These authors report the existence of cells in area 18 of the visual cortex that help to "extrapolate lines to connect parts of the stimulus which might belong to the same object" (p. 1261). They found these cells by using visual images that induce a percept of illusory figures in humans, as in Figure 2. Concerning the existence of a cooperative boundary completion process between similarly oriented and spatially aligned cells they write "Responses of cells in area 18 that require appropriately positioned and oriented luminance gradients when conventional stimuli were used could often be evoked also by the corresponding illusory contour stimuli" (pp. 1261-1262). This is explained in the BCS model by a feedback signal from the cooperative cell to the oriented edge representation at that same spatial location, as shown in Figure 3. The complete BCS model includes many additional spatial and orientational competitive mechanisms that are of less interest for our analysis.
In the context of curve detection, the cooperative cell of the BCS is not a specific curve detector in the sense of Zucker's model of curve detection [71], but rather a generalized curve detector which responds principally to colinear alignment, but will tolerate a range of gentle curvatures, although it does not distinguish between them. A single BCS cooperative cell therefore performs the function of a bank of curvature filters found in the Zucker [71] model. Hence, while the Zucker [71] curve detector is considered as a specialized feature detector tuned to recognize specific curved stimuli, the BCS boundary completion operation serves to reconstruct boundaries between oriented inducers, rather than to recognize the curves as features in their own right. In this sense, the response of the BCS represents a mirroring, or veridical facsimile of the visual input, recreated in terms of dynamic interactions between components of the visual system. The higher level representations used for recognition would presumably be defined in terms only of the points of high curvature, or the vertices, rather than their connecting boundaries. Indeed, it is the existence of the operation of boundary completion which obviates the need for an explicit representation of those boundaries by providing a mechanism capable of reconstructing the boundaries on demand, given the stimulus of the inducers at the vertices. In this sense, the boundary completion mechanism can be seen as an image decompression system for visual recall, converting the higher level vertex representation into a more veridical boundary representation.
One question raised by the above discussion is whether an explicit reconstruction or decompression need actually be performed by the visual system, or whether the compressed version alone suffices for internal use. If the vertices of a Kanizsa figure uniquely characterize that figure, and if the visual system has abstracted that figure to a representation of those vertices, then for what reason would the system need the veridical or decompressed representation? There is indeed much debate on this issue between those who profess that the visual system regenerates perceptions at a low level, for example when filling in data missing due to blind spots or scotomas [55, 56], and those who claim that a high level representation is sufficient explanation for the low level perceptions observed in the blind spot phenomena [8]. Without wishing to become entangled in this debate, we can say with some certainty that on the basis of the Kanizsa illusions alone, it is clear that whether or not the visual system requires a high resolution reconstruction of the illusory forms, it certainly does perform such a reconstruction based only on the vertices, and that this reconstructed figure is sufficiently veridical as to be virtually indistinguishable from an actual geometrical form defined by a luminance difference relative to the background. Indeed, na´ve observers often find it difficult to believe that such a luminance difference is not actually present in these illusions.
Kennedy [32] disputes the fact that illusory boundaries are indistinguishable from actual brightness differences seen in real figures. He quotes na´ve observers of these figures who report seeing a line that "doesn't exist", or that "isn't there", which would indicate that the observers can clearly distinguish illusory boundaries from real physical boundaries. It is not clear however whether the subject's reported perception is a property of the perceived boundary itself, or whether it is a function of the observer's cognitive expectation that the paper on which the figure is printed should not exhibit such subtle shades of brightness as seen in the Kanizsa figures. Kennedy also discusses three dimensional illusory figures generated by solid three dimensional constructions, which produce illusory boundaries that seem to float in empty space [32]. These figures were shown to children as young as three years old, who reported, in answer to questions, that the figures "cannot be touched" or were "made of nothing", or "made of air". Again, Kennedy concludes that the percept itself is therefore less real than a brightness difference occasioned by a real solid object. An alternative explanation remains however, that the children saw a "real looking" three dimensional boundary, but could see no physical object responsible for producing that boundary, and therefore acknowledged this apparent contradiction between their perceptual sensation and their cognitive understanding of the physical world by calling the anomalous boundary unreal. Indeed, a similar sensation is produced by reflections through a concave mirror, which can produce a "real image" in the optical sense, i.e. a point in space through which light rays cross, producing a full three dimensional image of an object floating in empty space. Optically, the image is real as the reflected object itself, although the perceptual contradiction makes the image seem ethereal or unreal, especially when it is occluded by a hand passing behind it.
Whether or not illusory figures are seen with exactly the same subjective sense of "reality" as real figures is open to question. Nevertheless, these figures do unquestionably produce a percept of brightness that is "real" enough to be measured psychophysically, both by comparison with a test patch, and by nulling experiments where the surface under the illusory form is presented somewhat darker than the surrounding areas in order to exactly cancel the brightness effect [61]. This clearly distinguishes such modal illusory forms, like the illusory triangles in Figure 2 from purely amodal percepts, like the missing "pie slices" of the three dark circles in Figure 2, which are seen to be occluded by the illusory triangle, and are thus perceived invisibly "behind" that figure. The missing arc segments can thus be imagined, but by no means "seen" with the same vividness as the occluding illusory triangle.
Kennedy [32] argues that the "apparent reality" of a figure is indicative of the level of representation in the visual system, which, if one accepts his contention that these figures are seen to be "unreal", would indicate that they are represented somewhat higher in the visual system than real brightness edges. Information theory suggests on the other hand that the quantity of redundant information, or high spatial detail, is a better measure of representational level in the visual system. The fact that the illusory triangle is seen in full spatial resolution, including a specific curvature along its edges in Figure 2 (B), and with a perceived brightness at every point over its entire surface, indicates that the higher level "cognitive" recognition of the triangle elicited by the vertices of the Kanizsa figure is transformed by the visual system into a high resolution (and therefore, by information theory, a low level) percept in the same format as an actual brightness percept of a real triangle, even if that percept is arguably somewhat less perceptually "real". An information theory interpretation of the Kanizsa figure therefore leads to the conclusion that the visual system does indeed perform a low level, high resolution reconstruction of perceived high level figures. In this context therefore, the BCS can be seen as a higher level abstraction or compressed representation of the luminance patterns represented in the retinal image, and the BCS / FCS interaction represents a "top-down completion" or decompression of higher level boundary abstractions to a low level, more complete spatial representation. Within the BCS model the cooperative cells can also be seen as a higher level abstraction of more complete information in the oriented representation, and the top-down feedback from the cooperative layer can be seen as a de-compression or "filling in" of the oriented information at the lower layer.
The properties of illusory boundaries can be studied in order to derive the computational properties of the visual mechanism. Two types of illusory boundaries are observed, those that perform a colinear or smooth curvilinear completion between visual inducers, and those that include a sharp kink or vertex between colinear segments. Psychophysical phenomena suggest that these two types of illusory boundary are related, in that they are seen to occur under similar circumstances, but that a continuous variation of the inducers from a colinear to a vertex configuration produces a sharp transition in the resulting illusory boundary, suggesting that two distinct mechanisms might be involved in the formation of colinear versus vertex boundary completion. In the next section I will discuss the properties of colinear illusory boundaries, and in the following section I will discuss illusory boundary completion through image vertices.
A colinear illusory boundary is seen to appear between visual inducers that are aligned so as to be easily connected by a straight, or nearly straight line. In the case of the Kanizsa figures, the illusory boundary will form parallel to the inducer where they meet, although under other circumstances such as the Ehrenstein illusion the illusory boundary tends to form orthogonal to the inducer, as will be discussed below.
The properties of the colinear illusory boundary has been studied in a number of quantitative psycho-physical tests. Figure 4 summarizes a number of these properties schematically. Shipley & Kellman [59] show that the salience of the illusory contour decreases as a function of spatial separation between the inducers, as suggested schematically in Figure 4 (A). Banton and Levi [2] show that the strength of the illusory contour is a function of the salience of the inducer, as measured either by the contrast of that inducer as suggested in Figure 4 (B), or the size of the inducer relative to the length of the illusory boundary, as suggested in Figure 4 (C). If the size of the inducers and the distance between them are increased proportionately, however, the salience of the illusory contour remains unchanged.
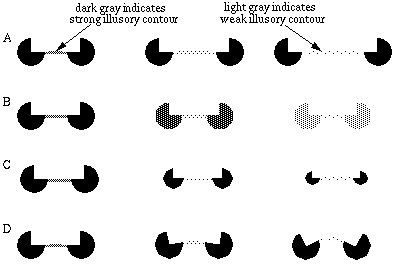
Factors that influence the salience of illusory boundaries, illustrated schematically: distance between inducers reduces salience (A); contrast of inducers increases salience (B); size of inducers relative to the gap to be completed increases salience (C); bending misalignment between inducers reduces salience(D).
Kellman & Shipley [31] show that the strength of the illusory contour varies as the angle between the inducers, as suggested in Figure 4 (D), as long as certain relatability criteria hold. These criteria were derived empirically from psychophysical studies of a number of inducer configurations, and are summarized schematically in Figure 5. The relatability criteria are defined in terms of the linear extensions to the inducers, as indicated by the dotted lines in the figure, and they note that illusory boundaries can only form when the extensions intersect at an obtuse angle, as in Figure 5 (A). If the inducers are parallel, but somewhat mis-aligned, as shown in Figure 5 (B), the extensions to the inducing edges will not intersect, and therefore the edges are not relatable. In fact, Kellman & Shipley note, that an illusory boundary can still be seen under these conditions, but only if the amount of misalignment between the inducers is very small, otherwise no illusory boundary will be seen with such a shearing mis-alignment. Finally, edges are not relatable if their extensions intersect only within the inducer, as shown in Figure 5 (C), i.e. the extensions are only defined beyond the inducers. It is interesting to note that relatable edges can be connected by a single inflection curve, as shown by the shaded line in Figure 5 (A), whereas non-relatable edges can only be joined by a double inflection curve, as shown in Figure 5 (B) and (C). I will refer to a relatable misalignment due to rotation of the inducers as shown in Figure 5 (A) as a bending misalignment, and a non-relatable misalignment due to translation, as shown in Figure 5 (B), as a shearing misalignment. Figure 5 (C) exhibits both a bending and a shearing misalignment.
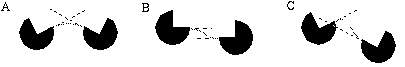
Relatability criteria defined by intersection of linear extensions of the inducers, illustrated schematically; relatable edges are those whose linear extensions intersect at an obtuse angle (A), non-relatable parallel inducers (B), non-relatable edges because the extension of one intersects the edge of the other, rather than the extension to the edge (C).
Illusory boundaries are also seen to project orthogonal to inducing lines, as illustrated by the Ehrenstein illusion, in Figure 6 (A). If each line of the Ehrenstein figure is considered as a long, thin rectangle, the short side of this rectangle is in fact parallel to the illusory contour, and thus could be considered to be the actual inducer in this case. Parametric studies by Lesher & Mingolla [39] however indicate that the salience of the illusory contour is not a simple function of the length of this short edge, which indicates that a separate orthogonal mechanism is involved in this case. Illusory boundaries are also seen to form at other angles besides exactly orthogonal, as shown in Figure 6 (B), although Nodine [46] shows that the salience of the resultant boundary is somewhat diminished. The illusory boundary therefore appears to be a function both of the local orientation of each inducer, and the global configuration of the inducers relative to each other. One possible explanation for this phenomenon derives from the fact that a line ending, such as those in the Ehrenstein illusion, stimulates oriented edge detectors through a range of orientations, producing a multi-orientation signal at the ends of the lines. An emergent global grouping then "selects" from the oriented responses only those that are consistent with the global grouping. This would explain why a small circular dot, which produces oriented responses uniformly at all orientations, can readily participate in a wide range of grouping phenomena. For example, Kanizsa [28] shows how lines of dots in smoothly curving configurations produce the percept of the smooth curves, as shown in Figure 6 (C). This property makes the small circular dot a very useful tool for the analysis of global groupings, because it factors the global grouping phenomenon from the bias introduced by the orientations of the local inducers. This property of the small circular dot will be exploited later to explore the global grouping phenomenon in the absence of the contribution of the local oriented signal.
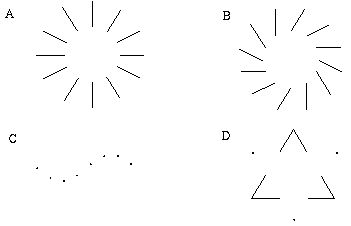
Ehrenstein illusion (A); angled Ehrenstein illusion (B); colinear grouping of a line of dots (C); illusory vertex completion through dots (D).
The grouping phenomena I have discussed so far all result in the appearance of a linear illusory boundary. A number of visual illusions result in illusory contours that define sharp vertices. For example the illusory triangle in Figure 6 (D) passes through vertices defined by the three dots. Kanizsa [28] shows that when curves defined by lines of dots are given excessive curvature, the percept of a smooth colinear grouping breaks into a percept of straight line segments joined by sharp vertices located at the dots, as shown in Figure 7 (A) where circles of dots of increasing curvature begin to appear as polygons. Wilson and Richards [69] present psychophysical evidence that the visual system uses two distinct mechanisms for the perception of gentle and steep curves. Subjects were presented with curves constructed of a parabola flanked by straight line segments, as shown in Figure 7 (B), and were asked to discriminate between two similar curves for a range of different curvatures. It was found that the accuracy of discrimination was greater for the more highly curved lines, with a sudden discontinuity at a certain curvature, suggesting that the visual system uses two separate mechanisms for the perception of gentle and steep curves. Lines of dots presented in similar curves illustrate the same phenomenon, as shown in Figure 7 (C), appearing to "break" into a sharp vertex at a certain curvature. These phenomena indicate that illusory boundary formation can occur in two modes, either completing smooth "colinear" curves, or through sharp vertices. The gradual transition between these two modes however suggests that a similar mechanism underlies both types of boundary completion.
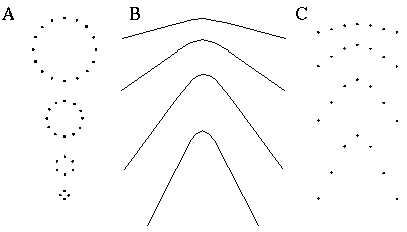
Circular grouping changes to polygonal grouping with increased curvature (A); curvature discrimination stimuli used by Wilson and Richards (B); colinear grouping changes to sharp vertex percept with increased curvature (C).
Another example of the unity of colinear and vertex boundary completion is provided by the minimal Ehrenstein figure shown in Figure 8,which can produce the percept of an illusory circle, square, diamond, or amorphous blob. It is interesting that in this figure the corners of the illusory square are not located by inducing dots, as in the case of the illusory triangle in Figure 6 (D), but appear spontaneously in a featureless region of the image.
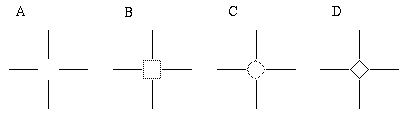
Ambiguous illusion with minimal Ehrenstein figure (A), with three commonly seen illusory forms (B, C, D).
The vertices defined by the illusory boundaries in Figures 6 (D), 7 (A) and (C), and 8 (B) and (C), all consist of an intersection of two illusory boundaries at that vertex. Illusory boundary completion can also occur through vertices defined by multiple orientations in a large range of combinations. Figure 9(A), (B), (C) and (D) shows arrangements of dots that produce illusory boundaries through vertices defined by one, two, three, and four dots respectively. A distance dependent relationship is seen in the grouping patterns of these dots, where the pattern defined by the nearest neighboring dots determines the percept of the vertex, and masks the groupings defined by more remote dots. For example, in Figure 9 (B) the horizontal grouping is masked by the stronger vertical grouping because the vertical distances are smaller than the horizontal ones. This phenomenon is discussed at length by Zucker et al. [70]. If alternate rows of Figure 9 (A) were removed, the horizontal grouping would emerge, showing that the horizontally adjacent dots are sufficiently close to generate a horizontal grouping, but that that grouping is masked by the nearer vertical grouping. Similarly, in Figure 9 (C) there are three nearest neighbors for each dot, which defines a three-way vertex passing through every dot in this pattern. If rows 2, 3, 6, 7, and 10 were removed from Figure 9 (C), a strong vertical grouping would immediately appear. Similarly, notice how Figure 9 (D) promotes a four-way grouping at each dot, suppressing an alternative diagonal grouping between the dots.

Illusory boundary formation through vertices composed of one (A), two (B), three (C), and four (D) oriented edges.
Two additional properties of illusory figures are worthy of note, and will be of significance in later discussions. First, illusory contours are seen to form inwards between inducers, but they are rarely seen to extend outwards beyond inducers. This phenomenon is seen clearly in Figure 9 (A), where an illusory boundary forms between pairs of dots, but stops abruptly at those dots. It is also seen in Figure 9 (B), (C), and (D) at the boundaries of those figures where the regular lattice of illusory contours between the dots is seen to end abruptly. This is the property of illusory boundaries that motivates the conjunctive constraint in the BCS model, that was discussed above.
Another property of significance to our discussion is the apparent occlusion of visual features behind an illusory figure, as seen in the Kanizsa and the Ehrenstein illusions. For example in the minimal Ehrenstein illusion, a cross shaped configuration is clearly recognized as being occluded behind a central illusory figure. The question for computer models of illusory phenomena is whether these amodally perceived objects should be represented as a part of the percept. The solution proposed by Grossberg and Mingolla [18] is to represent the modal and amodal percepts in separate layers of the system, where the amodal percept, represented by the BCS, would indeed encode the hidden figure as an explicit pattern of activation, whereas the modal percept, represented by the FCS would represent only the occluding form, corresponding to the visible percept of the image.
I have discussed illusory contour formation in terms of two types of boundary completion, colinear, which includes smooth curvilinear completion, and vertex completion. In the next chapter I will discuss neural network models of colinear boundary completion and problems that can arise in connection with these models. I will then propose a model of colinear boundary completion by a directed diffusion of oriented information in a neural network model, as an extension to the BCS model. I will show that the properties of this directed diffusion model are consistent with the properties of illusory contours as observed in the psychophysical studies. In the following chapter I will extend this model to handle the case of boundary completion through image vertices defined by a number of oriented edges that intersect at a point in the image. Figure 27.
Colinear boundary completion is a spatial operation that relates adjacent or nearby oriented edges which are found in an approximately colinear configuration. Colinearity between pairs of oriented edges can be defined as oriented signals that are at the same time parallel in orientation and spatially aligned in a direction that is parallel to that orientation. Figure 10 illustrates this principle. In Figure 10 (A), the barred circles represent two oriented detectors that are responding to a horizontally oriented edge at each location. The colinearity of these local edges depends on both the orientation of each local edge, and the locations of those edges with respect to each other. In this case, for example, colinearity of these edges can be detected by the fact that they are both horizontal, and at the same time horizontally disposed with respect to each other. This global colinearity relation between the two local edges is represented in Figure 10 (B) by the horizontally oriented detector which expects to receive horizontally oriented inputs, indicated by the barred circles, at two horizontally displaced locations, indicated by the dumbell shape.
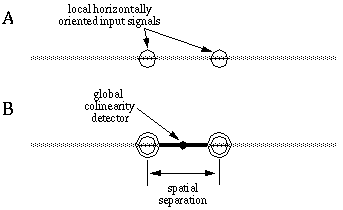
Colinearity between a pair of oriented inputs (A) implies that they are both parallel and spatially aligned, as suggested by the colinearity detector (B) which is sensitive to pairs of oriented inputs that are both parallel and aligned.
In a neural network model this spatial relation can be detected by a cell with a spatial receptive field that receives colinear input from nearby regions. The dumbell in Figure 10 (B) can be considered as a central cell whose receptive field is sensitive only to horizontally oriented input signals at a specific spatial separation. In fact, the detector depicted in Figure 10 (B) would be intolerant to any deviation from exact colinearity. The properties of illusory boundary completion discussed in the previous chapter indicate a considerable tolerance for small deviations from colinearity, so that a better model would allow a certain tolerance to deviation in both location and orientation of the input signals. This is the approach used in the BCS model, where the bipolar receptive field of the cooperative cell samples two nearby areas for appropriately oriented features. The distance between the sample points determines the separation over which boundary completion can occur.
Psychophysically, illusory contour formation is observed over a wide range of separations. In a neural network model this can be achieved in two ways. The system can be defined at multiple spatial scales, with cooperative cells defined at each of those scales, and, a spatial tolerance can be defined as a property of the receptive field, allowing it to respond over a range of spatial locations at each spatial scale. The BCS model employs a combination of both of these strategies, where spatial tolerance in the receptive field allows a single cell to perform boundary completion through a range of separations, and cells of different scales allow boundary completion through different ranges of separations. In this system therefore there is a trade-off between the spatial tolerance within each spatial scale, and the number of scales needed to cover the total range; the greater the tolerance within each scale, the less scales are required in the system as a whole.
At a single spatial scale, spatial tolerance in the receptive field implies that oriented inputs that are somewhat misaligned spatially from perfect colinearity can still produce a colinearity response, although the magnitude of that response should be diminished as a function of the misalignment in order to conform to the psychophysical data, as described in the previous chapter. This can be represented by a spatial spread in the receptive field of the cooperative cell, with a smooth fall-off in magnitude with spatial displacement, as suggested in Figure 11 (A). The psychophysical studies discussed above also indicate an orientational tolerance in illusory boundary completion, which can be represented by an orientational tolerance in the receptive field, as shown schematically in Figure 11 (B). In this figure each radial line represents a sensitivity in the receptive field to the orientation represented by that line, with a magnitude which is proportional to the length of each line. In both figures 11 (A) and (B), the spatial and orientational tolerance is depicted at discrete displacements and orientations for convenience, although in both cases the symbols represent a continuous response function through a range of locations and orientations, with a smooth fall-off in the response of the receptive field as a function of the deviation from the ideal displacement and orientation. The spatial and orientational tolerances can be combined in a single receptive field, as depicted in Figure 11 (C), which will perform colinear boundary completion through a range of spatial and orientational displacements. The spatial and orientational functions are however not independent, because the cooperative cell at a particular location represents an edge passing through that location, so that a deviation in spatial location requires a corresponding deviation in orientation in order to still pass through the center of the cell. For example, an oriented edge from the left that is displaced upwards would form colinear completion with an edge from the right, displaced downwards, with a common orientation that passes diagonally through the center of the cell at a diagonal orientation. The optimal input orientation could vary therefore as a function of spatial displacement in a radial manner from the center of the filter, as shown in Figure 11 (D). This radial input function is the one employed by the BCS model as originally defined by Grossberg & Mingolla [18], although different input functions have been proposed for smoother boundary completion. For example Cruthirds, Gove, Grossberg & Mingolla [personal communication] have proposed a parabolic input function, as shown in Figure 11 (E), which defines a smoother curve through the center of the filter.
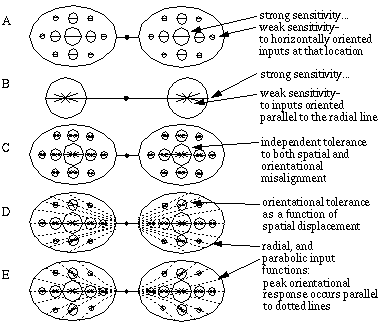
Input tolerances of the cooperative cell receptive field. Spatial tolerance only (A); orientational tolerance only (B); spatial and orientational tolerance (C); related spatial and orientational tolerance with radial input orientation fucntion (D); with parabolic input orientation function (E).
A smooth curve can be approximated well locally by a short line segment tangent to that curve. Even a cooperative cell with a strictly colinear receptive field therefore, as in Figure 11 (D) will produce a good match to smooth curves as long as the receptive field is small relative to the degree of curvature. The response of the cell to a curved stimulus will become increasingly sensitive however to small deviations of the curve from the idealized curvature encoded in the filter. In the case of the radial input function, that idealized curvature is defined by two straight line segments that meet at the center of the filter. This approximation will work well as long as the angle between the line segments remains small, i.e. for lines of low curvature. When the filter is used to complete steeper curves however, errors will be introduced expecially near the edges of the filter. For example, Figure 12 (A) illustrates a parabolic curve that passes throught the center of the filter tangent to the main axis of the filter. The local orientation of the parabola continues to match fairly well with the radial orientation lines near the center, but becomes progressively worse towards the periphery.
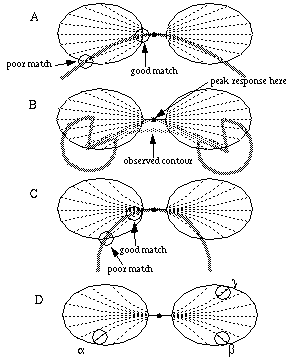
Error due to mismatch between input orientation function and actual curves, for a radial (A) and parabolic function (C), showing that the error increases with distance from the center. Error due to the radial input function which predicts the peak response at the intersection of the linear extensions of the inducing edges (B), although the actual illusory boundary is perceived somewhat below that point. Error due to the symmetry of the parabolic input function (D) which predicts an equal response from relatable inputs a and b, as for non-relatable inputs a and g. All of these errors become negligable when the size of the filter is small relative to the curvature of the boundary to be completed.
Another problem with this input function is that for all orientations but the central one parallel to the principal axis of the cell, the path defined by the input function experiences a sharp kink, or orientational discontinuity at the center of the cell. For example, this input function would produce a peak response when the center of the cell is located at the intersection of the linear extensions of the two inducing edges, as shown in Figure 12 (B), rather than somewhat below, where the illusory contour is observed. This can be accounted for by the orientational tolerance function, as will be discussed below.
The parabolic input function aleviates this problem somewhat because it represents a better match to a smooth curve rather than a sharp vertex. The match can only be perfect however when applied to a parabolic input. Figure 12 (C) for example shows that a circular arc segment matches well to the parabolic function near the center of the filter, but again, the match becomes increasingly worse with distance from the center of the filter. The parabolic input function introduces a more serious error however, due to the fact that the optimal curves defined in the two lobes of the filter are actually not independent, but rather the optimal curve in one lobe is determined by the input present in the other lobe. This is shown in the example of Figure 12 (D), where the presence of an oriented input a in the left lobe of the filter defines a parabolic arc through the center of the filter which is consistent with a boundary that passes through a point b in the right lobe of the filter. The essential symmetry of the filter however would dictate that an input g in the right lobe would produce an equally strong response in this cooperative cell. This is a violation of the relatability criteria of Kellman & Shipley, because inputs a and g are parallel but misaligned, and therefore should not produce an illusory contour, while a and b should.
Some of the problems described above can be aleviated by the orientational tolerance function, whereby the input need not match exactly the function defined by the filter at each location in order to produce an appreciable response in the cooperative cell. For example, in Figure 12 (A) an orientational tolerance would allow a large response for this configuration despite a certain orientational mis-match at the distal parts of the filter. The tolerance function could also account for the lower curvilinear boundary in Figure 12 (B).The tolerance function however introduces errors of its own to the system. Figure 13 (A) shows how a large orientational tolerance in even the radial input function would allow two oriented inputs related by a shear misalignment to produce a response in the cooperative cell in violation of the relatability criteria, resulting in an illusory contour with a double inflection curve. The magnitude of the observed shear misalignment tolerance, or the separation within which boundary completion can continue to occur through such a shear misalignment is a function both of the orientational tolerance itself, and the spatial scale of the filter. For example, Figure 13 (B) and (C) show two filters of different sizes but with the same orientational tolerance, to illustrate how the tolerance scales with the size of the filter. Kellman & Shipley [31] have determined psychophysically that the tolerance to shear misalignment is very small, on the order of 15 minutes of arc. This would indicate that either the orientational tolerance, or that the scale of the cooperative receptive fields must be small. A small orientational tolerance would lead to the other problems described above.
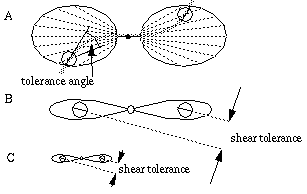
Error due to orientational tolerance for the radial input function which allows non-relatable inputs to produce a response (A); for a given orientational tolerance, the error is larger for larger scale filters (B) than for smaller scale filters (C).
Another problem relating to large scale receptive fields is a spatial averaging effect. When the area sampled by the receptive field is much larger that the region within which the input boundary is to be found, that allows a number of spurious signals to contribute to the response of that same cell, reducing the signal to noise ratio of that cell, and possibly introducing additional errors to the response of that cell.
All of the errors in the receptive field response of the cooperative cell described above are exacerbated when the degree of curvature to be completed is large relative to the size of the filter, requiring the use of peripheral regions of the receptive field, where the function is no longer a good approximation to a short line tangent to the curve at the center of the filter. The use of multiple spatial scales is unlikely to help in this case because the location of the center of the illusory boundary is determined by the large scale cell which spans the gap between the inducers, and the smaller spatial scales serve only to bridge the smaller gaps between the inducers and that central point. If an error at the largest scale results in a bad location for that central point, the smaller scale filters will also bridge to that erroneous location. All of these problems can however be diminished to negligible proportions by the use of small scale filters to perform boundary completion. The difficulty with the use of small scale filters lies in the conjunctive constraint, which requires that the filters be at least as large as the gap across which completion is to occur
In the next section I will discuss the feasability of performing smooth long range boundary completion by way of multiple local interactions through short range receptive fields whose spatial extent can be considerably shorter than the gap across which the illusory boundary must form. I will later discuss how the conjunctive constraint can also be implemented as a global emergent property of the local interactions between individual small scale filters.
Boundary Completion by Elastic Interactions
Grossberg [17] discusses the distinction between structural and functional scales in neural architectures by showing how large scale spatial functions of a neural network model do not necessarily imply large scale structural or computational components. Instead, the large scale phenomena can arise as emergent properties of small scale local interactions. This principle is exemplified by the behavior of the wooden spline. In the early days of wooden shipbuilding, flexible wooden splines were used to interpolate smooth curves between fixed reference points in the hull plan by fixing metal spikes at those reference points and bending the splines around them to define the curvature of the hull between those points. The early Gestalt theorists [40, 67, 68] favored this kind of mechanical analogy as models of visual perception, because a mechanism like a spline does not explicitly represent any particular geometrical form, but rather, that form emerges as a natural result of simple elastic interactions between local elements in the spline, which together produce a unified global pattern.
The operation of the spline is analogous to the smooth boundary completion process seen in illusory contours, where the large scale global curvature of the spline arises from the multiple local elastic forces in the spline. This suggests that local forces between small scale cooperative filters can in principle also lead to large scale globally smooth boundaries.
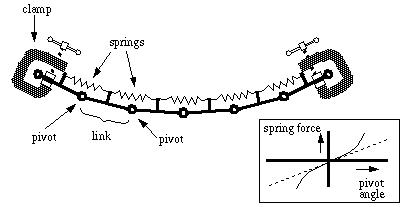
Finite element model of elastic spline for smooth boundary completion.
The physical response of elastic bodies under stress can be analyzed in computer models using the technique of finite element analysis [64], whereby an elastic object is modeled by a number of discrete rigid elemental components interconnected by elastic forces. In the limit, as the size of the elements is reduced while increasing the number of elements, the behavior of the finite element model will approximate the smooth analog behavior of the elastic body. Figure 14 represents a finite element model of a wooden spline, consisting of a segmented chain made up of rigid links that are connected by pivots. Springs spanning across the pivots are attached to the links on either side of the pivot, and apply a rotational force at each pivot which tends to hold the pivot straight, i.e. the spring is in its resting state when the angle between the links at the pivot is zero, and applies a restoring force due to extension or compression as a function of the angle between the links, as suggested in the sketch at the lower right in the figure. The clamps at the ends of the chain represent inputs that constrain the location and orientation of the terminal links, and thereby define the boundary conditions for the relaxation of the chain between them. Whether the spring function is linear or nonlinear, the chain will always relax into a smooth curve between those inducing end points, as long as the spring function is smooth and monotonic increasing. Furthermore, the shape of the resulting curve at equilibrium corresponds to the optimal configuration of the entire chain which minimizes the total deviation from straightness summed over the whole length of the chain. The spring function here acts as an error function in the measure of deviation from straightness, and that error function in turn acts directly on the chain in the form of a physical torque. A simultaneous relaxation of all the spring forces against each other which serves to minimize the total torque at each spring therefore serves also to minimize the total deviation from straightness of the chain. For example, if the spring function is linear, then the equilibrium configuration will minimize the sum of the angles between the links of the chain summed over the whole chain; if the spring function is quadratic, the equilibrium configuration will minimize the sum of the squares of the angles between the links, summed over the length of the chain. This system therefore can minimize the total deviation of the chain from straightness defined by any chosen error criterion by simply matching the spring function to the desired error function.
Finite element analysis with a relaxation algorithm has been used for pattern recognition by matching an elastic template to the visual input and deforming that template in order to minimize the differences between it and the input. Pentland et al. [50] demonstrate a relaxation scheme that matches an input to objects such as the human body or face by distorting the stored elastic template in such a way as to minimize the difference between it and the input to be matched. They state, however, that this system "is not suited to generalized object recognition where the object is not known a priori". In other words, their scheme can recognize only those forms for which a finite element model is defined, and cannot generalize to novel objects.
A more general class of finite element relaxation models is represented by the snakes model [29] which defines an elastic finite element spline (the snake) to represent a generalized smoothly curving boundary. The snake is applied to a visual edge in an image, and a relaxation algorithm then causes the snake to drift into a configuration that minimizes the difference between the snake and the visual edge, while respecting the internal stiffness constraints of the snake. In the simulations, the snake is seen to drift into position along the edge, spanning across missing boundary segments, while maintaining a globally smooth curvature. The snakes model has more general application than a specific finite element model such as that proposed by Pentland et al. [50], because the object represented by the snake, a smooth continuous curve, is a generalized feature that is encountered frequently in most natural images. The snakes model however is still too specific for a biological model of vision because several key parameters, i.e. the length of the snake, the number of snakes, and the initial position of the snake, must be determined a priori by the user.
A model such as the BCS can be considered to be an even more general example of a finite element model, in which the entire visual field can be considered to be populated by "potential snakes", and when a visual input is presented, some of the "potential snakes" become active, and begin to interact with one another, grouping into smooth curves. This model has the distinct advantage that it can represent any number of edges of any length and at any location in the image, and that the selection of appropriate snakes occurs automatically based on the features detected in the input image.
I will now present a model of boundary completion that inherits many of the properties of the BCS model, but performs long range boundary completion by way of small scale local interactions within the cooperative representation of the type illustrated by the finite element model described above. First, I will describe the principles of operation of the model, and show how it can perform boundary completion in a manner similar to the BCS. I will then show how it satisfies the conjunctive constraint by pooling of activation between inducers.
I will now present a model of illusory boundary completion by way of a diffusion of oriented information, with the properties of a generalized finite element relaxation model that performs long range boundary completion by way of short range local interactions. I will first describe the one-dimensional behavior of the model in order to illustrate the operation of the conjunctive constraint by local interactions along the line joining two inducers, after which I will describe the full two-dimensional model, with computer simulations that show how the properties of this model are consistent with the psychophysical properties of illusory boundary completion.
The directed diffusion model inherits many properties of the BCS model [18]. As in the case of the BCS, the directed diffusion model acts in concert with the Feature Contour System (FCS) [21] which represents a brightness percept that is influenced by the action of the directed diffusion model. Like the BCS, the directed diffusion model receives oriented input from a layer of orientation selective cells in which the signal from opposite directions of contrast has been summed, in order to produce an oriented signal that is insensitive to the direction of contrast. The directed diffusion model also performs boundary completion between oriented inducers by way of a cooperative / competitive feedback interaction in the orientational representation, producing the final boundary percept by way of a parallel relaxation between all of the forces active within the system, in a manner consistent with the Gestalt notion of analog field-like interactions between local elements. In the BCS model, the cooperative and competitive interactions are computed separately in cooperative and competitive layers, with a feedback signal to close the loop. In the directed diffusion model, all cooperative and competitive interactions take place within a single layer of the model, whereby the feedback occurs by virtue of the fact that the cooperative cells receive input directly from other neighboring cooperative cells, rather than from a previous layer. The cooperative layer of the directed diffusion model therefore represents a lumped version of the entire CC loop in the BCS model.
The principle of operation of the directed diffusion model is an oriented diffusion of cooperative activation outwards from each visual inducer in a direction that is parallel to the orientation of that inducer. Figure 15 (A) depicts two horizontal inducers that stimulate horizontal cells in the oriented layer, which in turn send activation to horizontal cells in the cooperative layer. Interconnections between cells in this layer propagate the horizontal signal in a horizontal direction by way of oriented receptive fields, generating a line of horizontally oriented activation in both directions from each of the two inducers. A pooling of activation between the inducers, shown in Figure 15 (B), fills in the illusory boundary between the inducers.
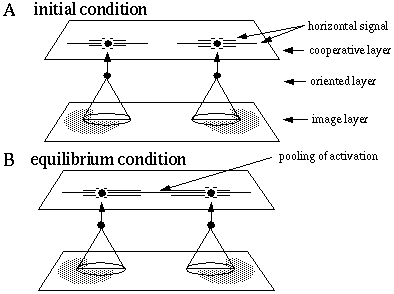
Two dimensional directed diffusion model. The horizontal input from the oriented layer generates a horizontally oriented response in the cooperative layer (A), which diffuses outward in a horizontal direction. Pooling of activation (B) between the inducers generates the illusory boundary.
In the computer simulations that will be presented in the next section, a standard diffusion equation is employed, i.e. the rate of change of activation in any cell is proportional to the difference in activation between that cell and the average activation of its neighbors, so that activation will tend to spread and diminish from the point of input. An equation of this type is presented below.
In order to allow completion of curved boundaries, a certain amount of "crosstalk" must be allowed between adjacent orientations. For example in Figure 16 (A), a horizontal cooperative cell located at the dotted elipse must be able to complete the curved boundary between the two angled fields of activation due to the angled inducers. In the proposed model this is accomplished by yet another form of diffusion of activation, this time between adjacent orientations at the same location in the cooperative representation, as shown in Figure 16 (B) and (C). For example, an isolated horizontal inducer would stimulate the horizontal cooperative cell at that location, represented in the middle layer in Figure 16 (B), resulting in a horizontal diffusion to neighboring regions. The activation of this cell will also partially stimulate the adjacent orientations at the same location, as suggested by the arrows to the upper and lower layers of Figure 16 (C). These cells in turn will propagate a somewhat attenuated signal outwards by diffusion to neighboring regions at their respective orientations. The combined effect of this orientational diffusion is a "fanning out" of the oriented signal by diffusion from an isolated inducer, as indicated in Figure 16 (C), which shows the total diffusion from a single horizontal inducer for three near-horizontal orientations simultaneously. The effect of orientational diffusion is somewhat similar to the orientational tolerance of the BCS cooperative cell, as defined by the input orientation term, which is the feature of the cooperative receptive field that allows it to receive oriented input directly from orientations other than that of the receiving cell.
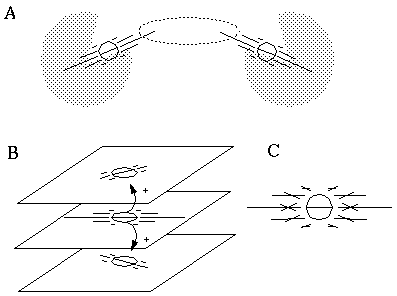
Orientational diffusion to adjacent orientations, producing orientational fanning.
In the system described so far, the broad receptive field profile of the cooperative cell will lead to a considerable spread of activation with distance from an inducer, resulting in broad, fuzzy illusory boundary formation. In the BCS model this kind of spatial blurring is compensated for by spatial competition in the CC loop which performs spatial sharpening along the peak of broad regions of activation. The competitive receptive field used in the BCS model is an isotropic on-center off-surround feedback interaction which performs spatial competition uniformly in all directions. A better choice for spatial sharpening is an anisotropic competitive interaction that suppresses activation only in a direction orthogonal to the represented orientation, so as not to counteract the competitive interaction in the oriented direction. This anisotropic receptive field can be combined with the cooperative receptive field in the simulations producing a compound receptive field that performs both cooperation (for directed diffusion) and competition (four boundary thinning) simultaneously in a single operation. Application of the anisotropic competitive interaction to the cooperative receptive fields produces the desired boundary completion and thinning of the boundaries, as will be shown in the section on simulation results.
The operation of this processing stage is reminiscent of the Rho Space model of Walters [65] which also attempts to explain the psychophysical phenomena of colinear grouping using a similar orientational cooperative / competitive architecture. The principal difference, as described by Walters herself, is that "the neural networks perform static, noniterative, discrete computations of the type that could be easily implemented in a clocked, discrete, parallel digital structure". Furthermore, Walters model does not make a distinction between the visible or modal percept, as modeled by the FCS, and the invisible, or amodal percept modeled by the BCS, and thus is a less complete model of the perceptual phenomena. Finally, the Walters model is insensitive to adjacent orientations, so that boundary completion around curves is not accounted for.
The purpose of the conjunctive constraint in the BCS model is to account for the phenomenon observed in visual perception that illusory boundaries only form inwards between two inducers; they will not develop outwards beyond an inducer into featureless space. If the large scale cooperative filters of the BCS model are to be replaced by multiple smaller scale filters, some means must be devised to communicate the conjunctive constraint between such cells across the gap between inducers in order to allow the growth of illusory boundaries only in those areas.
One solution to this problem is to allow "boundary completion" to extend outward from isolated inducers as in Figure 15 (A) and (B), but have such fields remain subliminal, or imperceptible, unless they are located between two inducers, and thereby receive activation from both directions, in which case they would become superliminal, or perceptible. This can be done, for example, by establishing a perceptibility threshold in the cooperative representation, in order to render the outward extensions subliminal and thereby imperceptible. An explicit perceptibility threshold however need not necessarily be postulated, since according to Grossberg [18] the grouping performed by the cooperative cells is by itself "invisible", i.e. produces no brightness percept, except by way of interaction with the FCS, where it may influence the diffusion of brightness signal. Since the outward extensions in Figure 15 (A) and (B) are "dead ends", i.e. they do not define an enclosed contour, the brightness signal in the FCS will be able to freely diffuse around them, and thus render them invisible. I will attempt to satisfy the conjunctive constraint therefore by defining a system which performs strong boundary completion inwards between inducers, and only weak boundary signals outward from inducers which generally remain invisible, so as to reproduce the appearance of the conjunctive constraint in conjunction with the FCS brightness diffusion. Sambin [58] proposes a similar scheme involving invisible fields of influence eminating from visual inducers, based on psychophysical observations of the distance dependence of interactions between visual elements.
There is one other aspect of this model that deserves mention at this point, concerning the issue of boundary effects at the edge of the simulation. Since the activation of a cell in this model is influenced by the activation in neighboring units, a special condition exists at the edge of the image, where the units have no neighbors. The purpose of this model is to perform illusory boundary completion between oriented inducers, and to suppress completion outwards from oriented inducers. For this reason, it is desirable to quench any stray outward boundaries such as those depicted in Figure 15, to prevent a boundary completion from occuring outward between the inducers and the edge. For this reason, the nodes at the edges of the simulation were clamped to zero activation. I will show however that in most cases this will have no practical influence on the performance of the model because, except in the case of zero decay, the outward diffusion decays away with distance from the inducer, and thus would have tapered off to nothing anyway.
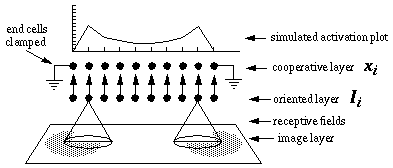
Layout of one-dimensional directed diffusion simulations. Oriented edges in the image layer activate cells in the oriented layer by way of oriented receptive fields, and the oriented cells in turn stimulate cells in the cooperative layer at those locations. A diffusion of oriented activation in the cooperative layer then spreads the activation outwards from the inducers, as suggested by the simulated activation plot, shown above.
The following simulations represent a one-dimensional line of cooperative cells that lie in a straight line across one or more oriented inducers in a direction parallel to the orientation represented by those inducers, as illustrated in Figure 17. The oriented cells receive input from the image layer by way of oriented receptive fields, and communicate activation upward to the cooperative layer. The plot at the top of the figure shows the activation of those cooperative cells at equilibrium in response to the applied inputs. The cells at either end of the cooperative layer are clamped to zero activation. The cells within the cooperative layer receive input from both the oriented layer, and from each of their adjacent neighbors in the cooperative layer and respond according to the diffusion equation
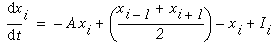
|
(EQ 1) |
where xi represents the activation of the ith cooperative cell, A is the decay rate (a small positive constant), and Ii represents the input from the ith oriented cell. This equation is a diffusion equation because it tracks the difference between the activation of the cell xi, and the average activation of its two neighbors. In the absence of input Ii, if the activation xi of the ith cell is less than its neighbors, then its activation will grow, whereas if it is greater than its neighbors it will decay. This will tend to spread any pattern of activation (or clamped inactivation) outward from the source, as in the FCS diffusion.
Equation 1 is a linear differential equation that describes the activation of a neuron i as a function of the activation of its immediate neighbors i-1 and i+1. The use of a linear equation is questionable in the context of neural activation because it predicts that the neuron's activation can grow without bound as the input grows without bound. This choice, however, simplifies the analysis and reduces the computational load of the simulations. Furthermore, as I will discuss later, the results that follow should hold when a more realistic activation function is used. In fact, a similar computational simplification has been used to describe the diffusion process in the FCS model [21].
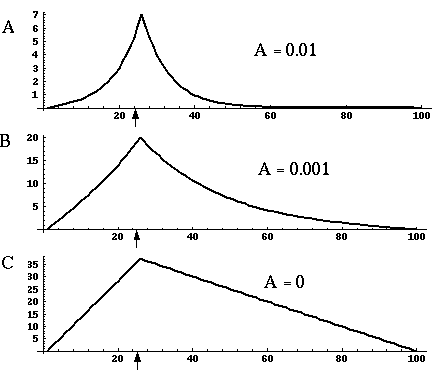
Directed diffusion simulation with a single input and various decay rates. The high activation due to the input located at the arrow spreads outward in both directions by diffusion. In the case of zero decay, the activation spreads all the way out to the clamped nodes at the ends of the simulation.
Figure 18 (A)shows the result of a simulation of this system with 100 nodes in the cooperative layer and a single oriented input of value 1.0, (indicated by the arrow in the figure) and a decay rate of 0.1. At equilibrium, a peak is observed at the location of the input, with a spread of activation in either direction, tapering away with distance from the inducer. If the decay rate is reduced to 0.01, as in Figure 18 (B), the activation spreads a greater distance from the inducer in both directions. With the decay constant reduced to zero, the activation spreads linearly in both directions to the clamped nodes at the ends of the display, which are clamped to zero activation. Examination of the equilibrium state of the diffusion explains this behavior. The equilibrium value of a node xi is given by
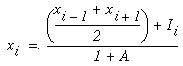
|
(EQ 2) |
This equation assumes that the neighboring node values xi-1 and xi+1 remain fixed, i.e. this is a local equilibrium. If = Ii zero, and the decay rate is zero, Equation 2 shows that such a node will equilibrate to the average value of its two neighbors, assuming that they themselves remain fixed. In fact, of course, a change in the value of the ith node xi will directly influence the both the activations xi-1 and xi+1. Nevertheless, at the global equilibrium, the local equilibrium condition of Equation 2 will hold for all nodes with respect to their neighbors. If all the nodes between the inducer and the clamped nodes at the ends in Figure 18 (C) satisfy this equation, then at the equilibrium of the whole system, their activations must define a straight line that performs an interpolation between the value of the node over the inducer and the activation of the clamped nodes, which are held at zero, as seen in Figure 18 (C). The deviation from this linear interpolation seen in Figure 18 (A) and (B) due to a non-zero decay rate leads to an overall lowering of activation as well as a faster spatial decay. This result suggests that in Figure 18 (A) the activation pattern due to the single input must spread all the way to the clamp points, i.e. node 99 must be greater than zero when full equilibrium is established, even though its actual value may be exceedingly small. In practice however the actual range of such spatial diffusion will be limited by the mathematical precision of the simulation, i.e. beyond a certain distance from the input the activation value becomes so small as to be rounded to zero in the computer, and further spread of activation is quenched. A similar roundoff would also occur in a biological implementation when the activations of the nodes that are far enough from the input become so low as to be lost in the noise of baseline activation. The range of diffusion in such a system therefore is mathematically infinite, but practically finite.
The set of simulations that follow explore the phenomenon of pooling of activation between pairs of inducers. Figure 19 (A), (B) and (C) plot the equilibrium values of cooperative cells in response to two inducers at the same separation but with decay rates set to 0.001, 0.0001, and 0.0 respectively. The pooling effect can be seen in the activations of nodes that are between the two inducers, which remain higher than they would be due to either inducer alone. The effect is particularly pronounced with low decay rates, and becomes "perfect pooling" with a zero decay rate, where the activations perform a linear interpolation between the activations at the two inputs. With a non-zero decay rate however the activations of the nodes between the inducers falls off non-linearly with distance from the inducers, reaching a minimum at the midpoint. This distance dependent decay determines the range across which boundary completion can occur. The directional diffusion model predicts that a shorter illusory boundary will also form outwards from the two inducers, as well as the stronger illusory boundary that forms inwards between the inducers, as seen in the decaying pattern of activation between the inducers and the clamped endpoints.
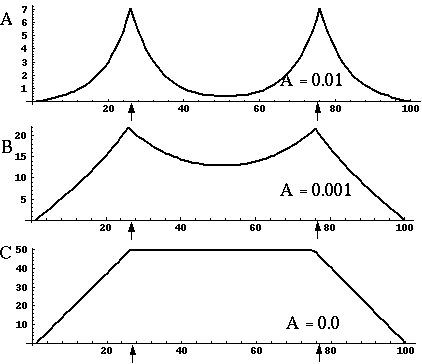
Effect of decay rate on the range of boundary completion between two inducers. With a zero decay rate, the boundary performs a linear interpolation between the activations at the two inducers, marked with arrows.
In the following section I will show that this model makes several predictions that are in qualitative agreement with psychophysical studies by Shipley & Kellman [59] and Banton & Levi [2], that indicate that the salience of the illusory boundaries in a Kanizsa figure diminishes as the distance between the inducers is increased. Furthermore, the salience increases with the "strength" of the inducing edges, whether measured as the length of the edge, or the contrast across that edge. I will now show that the directed diffusion model is consistent with these findings.
Figure 20 shows the behavior of the system in response to two inputs as the separation between the inducers varies in the range of 50, 40, 30, and 20 nodes for Figure 20 (A), (B), (C), and (D) respectively. The simulations show that the strength of the illusory boundary diminishes steadily with distance between the inducers. This can be seen by the diminishing height of the plot of activations between the inducers. This is shown graphically in Figure 21, which plots the equilibrium activation of the node that is midway between the two inducers, i.e. where the boundary is the weakest, for a set of simulations using the same parameters as above, as the separation between the inducers is varied.
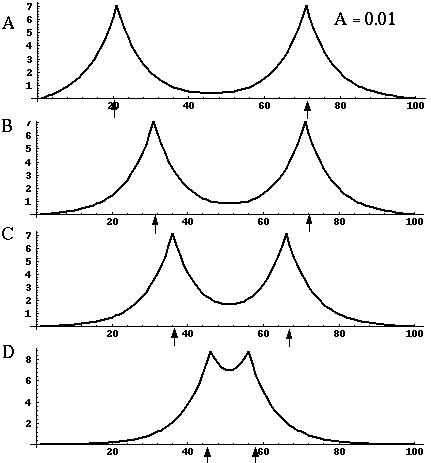
Simulation of pooling of cooperative activation between two inducers, showing how the salience of the illusory boundary, indicated by the height of the activation plot between the inducers, diminishes with separation between the inducers.
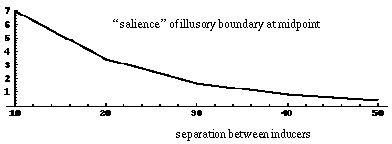
Plot of "salience" of illusory boundary measured at its midpoint, as a function of the separation between two isolated inducers.
Psychophysical studies by Banton & Levi [2] indicate that the salience of illusory boundaries is also a function of the contrast of the input stimulus, the greater the contrast, the more salient the resultant illusory boundary. Greater contrast of the oriented inducer would translate to a larger magnitude in the response of the oriented cells of the system. This is illustrated in Figure 22 (A), (B), and (C), which plot the response of the directional diffusion system to two oriented inputs of magnitudes 1, 2, and 3 respectively, resulting in progressively greater activations along the entire length of the illusory boundary.
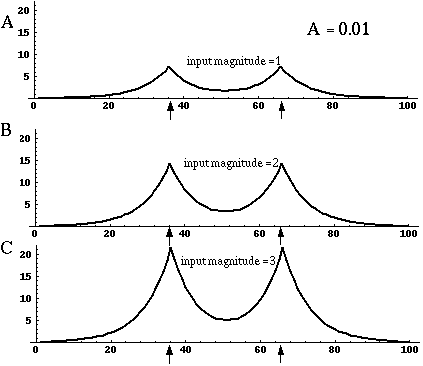
Effect of contrast, as represented by the input magniutde, on the salience of the illusory boundary, showing that the salience of the illusory boundary, as indicated by the height of the plot between the inducers, is increased as the input magnitude varies through one (A), two (B), and three (C).
Psychophysical studies by Shipley & Kellman [59] and Banton & Levi [2] also show that the salience of the illusory boundary is a function of the length of the oriented inducer, a longer inducer producing a more salient illusory boundary. Figure 23 (A), (B), and (C) show the response of the directional diffusion system in response to inputs of magnitude 1, but with a spatial extent of one, two, and three adjacent nodes respectively. Due to the pooling of activation between adjacent nodes, the local response to such adjacent inducers is not only spread out, but produces a peak of greater magnitude than the response to isolated inducers. This results in a more salient illusory boundary, or a greater range of boundary completion, as seen in the psychophysical studies.
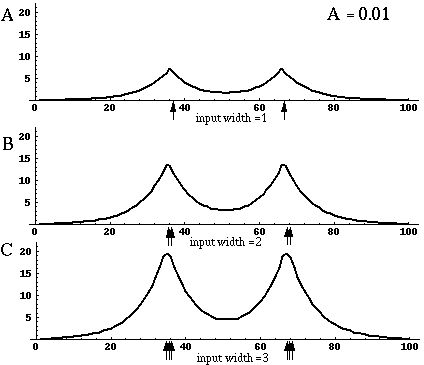
Effect of spatial extent of inducer on the equilibrium activation value. The arrows indicate input signals with a width of one (A), two (B), and three (C) pixels, showing how the height of the plot, indicating salience, and the spatial extent of the diffusion, both increase with the width of the input stimulus.
Finally, psychophysical studies by Kojo, Liinasuo, & Rovamo [36] indicate that the same factors that were found in the other studies to increase the salience and range of illusory boundaries, i.e. greater length of the inducers, and less separation between inducers, were also found to increase the speed with which the illusory boundaries are perceived, presumably as a result of a faster propagation of the illusory boundaries between the inducers. This phenomenon is also consistent with the directional diffusion model because a higher peak of activation will result in a faster rate of diffusion, as shown in Figure 24. In this figure, inputs of various magnitudes are presented for a fixed interval of time, 100 time units in this case, rather than allowed to run to equilibrium, after which time the range of the spread of activation was measured at some arbitrary perceptibility threshold (50 was chosen in this case) indicated by the horizontal dotted lines in the figure. It can be seen that the smaller magnitude inputs have not spread as far in these 100 time units as have the larger magnitude inputs, indicating that the rate of diffusion of activation is a function of the magnitude of the input. Since we have shown in the previous experiment that a longer input stimulus also results in a greater magnitude of activation, this result generalizes to the conclusion that longer inputs will also spread activation faster than shorter inputs of the same magnitude, as was found in the psychophysical studies.
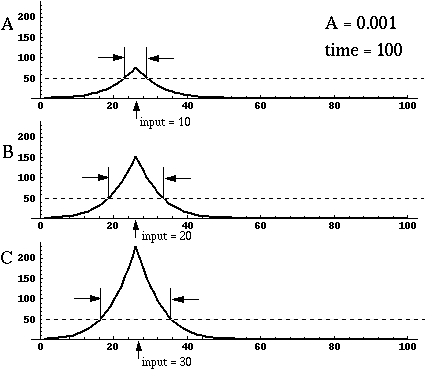
Effect of input magnitude on speed of diffusion. In these simulations the system was not allowed to run to equilibrium, but instead only to 100 iterations. In that time, the range of the illusory boundary was measured at a threshold of 50, showing that a larger contrast input, indicated by a larger input magnitude, propagated a greater distance in the same time than a smaller input magnitude, through a range of 10 (A), 20 (B), and 30 (C) arbitrary units corresponding to spiking frequency.
The foregoing simulations have revealed that the directional diffusion model can explain certain significant properties of illusory boundary formation. Specifically, the directional diffusion model shows that global boundary completion can be achieved by way of purely local interactions between units, as can the conjunctive constraint, so that the large scale receptive fields seen in the BCS model are not required to reproduce these large scale phenomena. Furthermore, the fine-grained architecture of the directional diffusion model avoids some of the problems that result from the large and complex receptive fields of the BCS. The directional diffusion model is also consistent with a body of psychophysical data on illusory boundary formation, specifically that illusory boundary salience, completion range, and completion speed are a function of inducer length, inducer magnitude (contrast), and inducer proximity. I will now demonstrate how the directed diffusion model can be extended to two dimensions, and will present simulations of the two dimensional system.
The architecture for the two-dimensional simulation of the directed diffusion is depicted in Figure 25. An input image is projected onto the image layer which consists of a two dimensional matrix of cells Ixy. Cells Oxyr in the oriented layer receive activation from the input layer by way of oriented receptive fields centered at location (x,y), and with orientation r. This is accomplished by way of spatial convolution of the input image with the oriented filters, such that
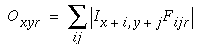
|
(EQ 3) |
where Fijr is the oriented edge detector. The absolute value function in this equation implements the insensitivity to direction of contrast proposed for the BCS model.Twelve orientations were represented in this manner in the simulations (only four are shown in the figure for simplicity) which corresponds to twenty-four possible orientations in a full contrast image. In the directed diffusion simulation, this oriented image convolution was bypassed, and instead, a simulated oriented image was applied directly to the oriented layer, in the form of individual points of oriented activation in the oriented layer, simulating the response of the oriented layer to an isolated oriented edge in the input layer. While in nature, such an isolated oriented signal would never be found, this approximation was sufficient to demonstrate the properties of the orientational interactions due to directed diffusion.
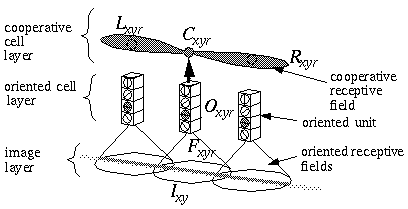
Directed diffusion simulation architecture. Oriented edges in the image layer stimulate activation in oriented cells of the oriented layer by way of oriented receptive fields. The oriented signal is then propagated up to cooperative cells at the same location. The cooperative cells also receive input from adjacent cells of like orientation in the same cooprative layer, resulting in a feedback interaction within the cooperative layer.
Oriented cell activation is collected by the left and right lobes of the cooperative cel receptive fields, described by the functions L and R as defined below.
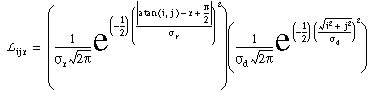
|
(EQ 4) |
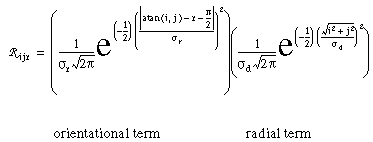
|
(EQ 5) |
Each of these terms is made up of a product of two Gaussian functions. The first Gaussian, referred to as the orientation term, is a function of deviation from the central orientation r, with a standard deviation of sr. This function produces a peak along a line of orientation r. The second Gaussian, known as the radial term, decays with increasing spatial separation from the center of the filter. The product of these two terms defines a two-dimensional oriented receptive field that extends outward in the oriented direction.
The only difference between the equations for L and R is in the exponent of the orientational Gaussian term, which determines the direction of the receptive field, such that the orientations of L and R differ by p. The arctangent function used in these equations is the two argument atan2 function, as defined by :
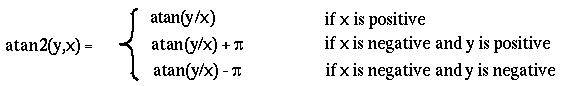
A cooperative cell Cxyr at location (x,y) and of orientation r receives input both directly from the oriented cell Oxyr at location (x,y) and orientation r, as well as through the "left" and "right" lobes of its bipolar receptive field Lxyr and Rxyr from adjacent cooperative cells of the same orientation:
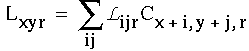
|
(EQ 6) |
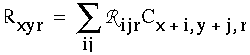
|
(EQ 7) |
The resultant activation of the cooperative cell is governed by the differential equation
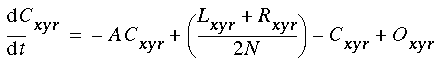
|
(EQ 8) |
In this equation, the first term is the passive decay term governed by the decay rate A, a positive constant. Following this is a difference of two terms that represents the difference between the activation of the cell Cxyr and the average activations in the regions of the cooperative layer governed by the left and right lobes of the cooperative receptive field, where N is a normalizing constant. In the absence of direct input from the oriented layer, this differential equation tracks the difference terms to equilibrate at an activation between the average activations in the two lobes. As for the 1-dimensional case, if the decay term A is zero, the equilibrium point is exactly midway between the neighboring activations, resulting in a linear interpolation. The last term in Equation 8 is the direct input from the oriented layer, which biases the equilibrium state towards the pattern of activation present in the oriented layer. In the computer simulations, the equilibrium value of Equation 8 was used, which is in the form
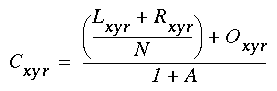
|
(EQ 9) |
I have mentioned earlier the necessity for a certain cross-talk between adjacent orientations in order to account for curved boundary completion, as suggested in Figure 16. In the two-dimensional simulations this was accomplished by a certain diffusion of the oriented filter response between adjacent orientations. First, the filter response is computed for each oriented filter as described in Equations 6 and 7, i.e. each oriented filter receives input exclusively from like oriented cooperative cells. Then, the filter response is modified by an orientational blurring with adjacent oriented responses at that same location, using the formulae
|
(EQ 10) |
|
(EQ 11) |
which were evaluated at each iteration, where f is a small positive diffusion function. In this manner, for example, a strong horizontal oriented response would stimulate a weaker response in both adjacent orientations, and in the next iteration those adjacent responses would diffuse to more distant orientations with still further diminished magnitudes, as suggested in Figure 16.
The spatial competition required for thinning of the illusory boundaries was accomplished by replacing the orientational Gaussian term of Equations 12 and 13 with an orientational difference of Gaussians, which produced inhibitory side-lobes flanking the excitatory orientational peak on either side. In other words, equations 12 and 13 were replaced by
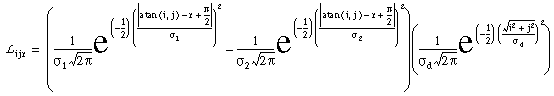
|
(EQ 12) |
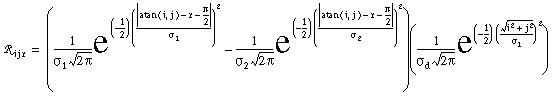
|
(EQ 13) |
The mathematical shape of these receptive fields is depicted in Figure 26 (A), where the background gray denotes zero filter values, while lighter shades denote positive values, and darker shades denote negative values. The figure shows both the "left" and "right" receptive fields for a horizontal cooperative cell in one plot, to indicate the total field of influence of a single cell. In the computer simulations, the actual field used was further quantized as illustrated in Figure 26 (B). Note that the two pixels that are horizontally adjacent to the central pixel of the filter have near zero values. This is an effect of the quantization, as shown in Figure 26 (C), which depicts a magnified section of that field just to the left of the center of the function. The central pixel and the pixel to its left average between both positive and negative functional values, resulting in a near zero sum. It is only when the width of the central excitatory lobe approaches the width of a pixel that the resultant value averaged over the area of the pixel becomes significantly positive. As will be seen in the next section, this quantization error has a small influence on the simulation results, without however affecting the general properties of the model.
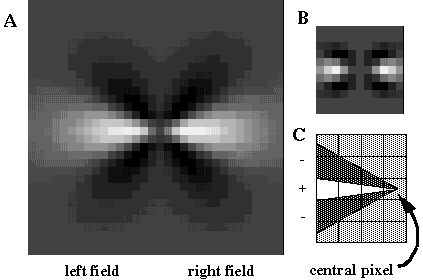
Receptive field profile for directed diffusion cooperative cell with inhibitory side-lobes.
Figure 27 shows the results of a computer simulation of the directed diffusion system, where the activation in the cooperative layer is plotted in response to two horizontal inputs at various separations. The level of cell activation is denoted by the darkness of the gray shade in these plots, with darker pixels representing higher activation. Figure 26 (A), (B) and (C) show the equilibrium activations for inputs separated by 10, 15, and 20 pixels respectively, with a decay rate value of A = 0.01. The location of the inputs is visible as a pair of very dark pixels, surrounded by horizontal regions of activation that they stimulate. Note that the pixels immediately adjacent to the most active nodes over the inducer exhibit less activation than pixels that are somewhat farther away. This is an effect of the quantization discussed in the previous section, whereby the cooperative receptive field values are near zero immediately adjacent to the central pixel of the filter. In a finer scale simulation this effect would be absent. Note that the salience of the illusory boundary as measured by the activation levels of the cells located between the inducers diminishes as the separation between the inducers is increased, as observed in the psychophysical data reported above. Also, boundary completion is seen to occur over distances greater than the size of the receptive field of the cooperative cell, which spans five pixels in each direction from a central pixel.

Directed diffusion system response to two parallel oriented inputs as a function of separation between the inducers.
Figures28 (A), (B) and (C) show the response of the cooperative cells to two oriented inputs as a bending misalignment is applied. The strength of the illusory boundary is seen to diminish smoothly as a function of the angle of the misalignment. According to the relatability criteria of Kellman & Shipley [31] the inducers remain relatable until the angle between them becomes 90 degrees, at which point they become abruptly non-relatable. In this model the illusory boundary fades away continuously with increasing angle between the inducers.

Directed diffusion system response to two oriented inputs as a function of angle between the inducers.
Figure 29 (A), (B) and (C) show the response of the cooperative cells to two oriented inputs as a shearing misalignment is applied, i.e. as the parallel inducers are shifted laterally relative to one another. The shear varies from zero in Figure 29 (A), two pixels in Figure 29 (B), and three pixels in Figure 29 (C). The strength of the illusory boundary is seen to diminish rapidly even at very small shear values, as noted by Kellman & Shipley [31]. The illusory boundary disappears completely at a shear of only three pixels.

Directed diffusion system response to two parallel oriented inputs as a function of stagger, or lateral shift between the inducers.
I have described a model that is similar to the BCS, that performs two-dimensional boundary completion between oriented inducers in a manner consistent with psychophysical observations of the formation of illusory boundaries. The mechanism I propose generates these illusory boundaries as an emergent property of local interactions between individual elements in the system in a manner that is consistent with the field-like interactions suggested by Gestalt psychology. In the next chapter I will discuss the issue of image vertices where multiple orientations are present at the same spatial location. Both the BCS and the directed diffusion model have difficulty with this condition, because of competition between orientations at a single location. The model I will present in the next chapter will address these issues, and will lead to many more predictions of perceptual phenomena.
In chapter 2 I presented a neural network model that performs illusory boundary completion in a colinear, or smooth curvilinear manner that is consistent with observed psychophysical data. I have shown earlier in chapter one however that certain visual illusions indicated that boundary completion can also occur through image vertices consisting of some number of edges that meet at a point. In this context, the colinear boundary can be seen as a special case of a vertex composed of two edges separated by 180 degrees which meet at the center of the vertex. In this chapter I will show how the mechanism of directed diffusion can be extended to perform both colinear and vertex completion with a single mechanism by way of harmonic interactions in the orientational representation that promote orientational periodicity of edges that meet at a vertex. I will show that this mechanism predicts many properties of vertex completion that are consistent with perceptual grouping. Finally, I will show that this model leads to compression of information of the type discussed by Attneave.
The directed diffusion model presented in the previous chapter was designed specifically to perform boundary completion along a straight line or curved edge. Specifically, oriented input in one lobe of the bipolar receptive field propagates oriented activation in the direction of the other lobe. The shape of the cooperative receptive field can thus be considered as a "template" of the idealized colinear vertex. A similar observation can be made about the BCS model.
In order to generalize colinear boundary completion to perform vertex completion, cells can be defined whose receptive fields represent different vertex types defined by the intersection of one, two, three, or more edges that intersect at a point in a variety of different angular configurations. For example, Figure 30 (A) illustrates a cell that represents an "L" vertex defined by the intersection of two edges separated by 90 degrees. In this vein, Grossberg & Mingolla [19] propose such specialized receptive fields for boundary completion through image vertices. A large number of vertex patterns would have to be represented at each spatial location, and each of these receptive field combinations would have to be reproduced at all orientations, just as in the case of the colinear cell. Figure 30 (B) illustrates the combinatorial explosion that can result from a representation of every combination of any number of edges at all possible orientations. It may be possible to alleviate this problem by compression or coarse coding, e.g. by allowing each pattern to represent a range of similar patterns, in the same manner that the colinear cell in the directed diffusion model represents a range of smooth curvilinear edges besides the strict colinear one of a perfectly straight edge. Even with coarse coding however, the representation of vertices by way of specific cells with hard wired receptive fields represents a combinatorial expansion in the representation, similar to the curvature representation of the Zucker [71] model.
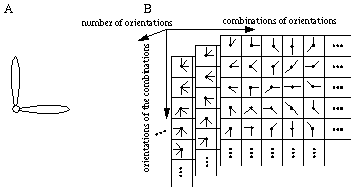
The representation of multiple orientations at a single spatial location by way of specialized receptive fields, for example a right angled vertex detector (A), and a combinatorial assembly of other vertex representations (B).
Heiko Neumann [44] proposes a more general solution in the form of a "rosette" of receptive fields at every orientation, as shown in Figure 31, with a separate cell body receiving input from each of the oriented monopolar receptive fields. The conjunctive constraint is implemented in this model by a requirement that at least two cells must receive oriented input in order to allow boundary completion through the vertex. This mechanism is able to perform boundary completion around vertices of any combination of two or more orientations. One problem with this model is that it does not account for boundary completion through a vertex defined by a single oriented edge, of the type shown in Figure 9 (A), where a boundary is seen to form between two adjacent dots, but it does not extend beyond those dots, so that the vertex defined at each dot consists of one edge only. Furthermore, in Figure 9 (B), (C), and (D), this model would predict boundary completion to all adjacent dots, not just the ones that are immediately adjacent, so that the vertices in Figure 9 would all appear as stars made up of a great number of orientations. A full model of vertex completion would have to account for the distance dependent behavior discussed in Chapter 1.
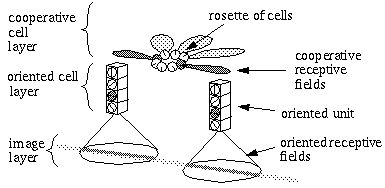
Architecture of the generalized cooperative cell, or "rosette" of cells around a central vertex, each of which received oriented input only from one direction and orientation from that vertex, so that different vertex configurations are represented by particular patterns of activation in the ring of cells.
An advantage of Neumann's "rosette" model is that orientational combinations are no longer encoded by hard-wired receptive fields, but rather they are represented by patterns of activation in the ring of oriented cells. Boundary completion in this architecture therefore consists of the completion of particular patterns of activation in the oriented cells. The question remains however which of the many possible particular vertex patterns should be completed for a specific input stimulus, and what computational architecture might be responsible for performing such a completion.
An interesting view on this problem can be found again in Attneave's discussion of information theory [1]. Attneave suggests that the Gestalt principles of perceptual grouping represent patterns of regularity or redundancy in the visual world. In the context of Neumann's rosette model, regularity can be seen in the orientational representation as a periodicity of the oriented signal around the ring of cells. This periodicity can be encoded by a Fourier decomposition of the pattern of activation in the orientational representation, as suggested by Figure 32. For example, a vertex consisting of four edges equally spaced in a "+" vertex would be represented by the fourth coefficient of the Fourier series, because the edges subdivide the full circle into four equally spaced segments, representing an orientational frequency of four edges per cycle. A three way vertex with arms separated by 120 degrees would be represented by the third coefficient. A straight line through the vertex would be represented by the second coefficient, corresponding to the periodicity of two edges separated by 180 degrees. A vertex defined by a single orientation extending in one direction from the vertex represents the first coefficient of the Fourier series. The zeroth coefficient represents the DC term of the Fourier transform, i.e. a feature consisting of orientations in all directions simultaneously representing the overall magnitude of the oriented signal at all orientations. This coefficient corresponds to a small circular dot centered at the vertex, which would stimulate cells of all orientations simultaneously. The first five harmonics from R0 to R4 and the vertices that they represent are depicted in Figure 32. These harmonics represent the first five terms of a circular harmonic series that can be used as a descriptor for the configuration of lines joined at a vertex. One advantage of a harmonic representation is that the translation invariance of a linear Fourier representation corresponds to a rotation invariance in circular Fourier representation, so that each coefficient represents the corresponding vertex pattern in a rotation invariant manner.
Decomposition of orientational combinations into a Fourier series of orientational frequency showing the Fourier coefficients, the corresponding pattern of orientational activity, the vertex pattern represented by that coefficient, and the symmetry of each harmonic.
The rotation invariance of this representation also represents a form of information compression, owing to the fact that each coefficient, represented by a single value, corresponds to an entire pattern of orientational activity, and the rotation invariance means that all rotations of that same pattern correspond to the same Fourier coefficient. Notice also that the periodicity in the orientational representation corresponds to a measure of the symmetry in the represented pattern, as shown on the right in Figure 32. This is consistent with Attneave's observation that symmetry represents a redundancy in the visual world for the purpose of information compression.
Other vertex combinations besides those represented by the first five harmonics of the Fourier series can be obtained by combinations of the harmonics, as is true for any Fourier representation. Figure 33 shows the harmonic combinations that represent the "L" vertex (A), the "V" vertex (B), and the "T" vertex (C). For example, by analysis or simulation, one can see that the "L" vertex results from a combination of R1, R3 and R4. Note the similarity to the "V" vertex, which is composed of R1, R2 and R4. In fact, the relative magnitudes of the second and third coefficients will determine the exact angle between the two arms of this figure.
Construction of additional vertex types by combinations of the harmonics. The "L" vertex is composed of the first, third, and fourth harmonics (A), the "V" vertex is composed of the first, third, and fourth harmonics (B), and the "T" vertex is composed of the first four harmonics (C).
A number of different mechanisms can be proposed to implement a Fourier filtering of the orientational signal, which requires a boosting of the orientational periodicity in the oriented signal in the cells of the rosette of cooperative cells. Grossberg [17] has shown that periodicity in a neural network architecture can be achieved by a recurrent cooperative-competitive field of neurons connected by spatial receptive fields with an on-center, off-surround profile.
An alternative scheme is suggested by the fact that a simple harmonic resonance, such as an acoustic wave in a resonant cavity, automatically performs a Fourier filtering of exactly the sort required in this model. Portnoff [52] has shown that sound waves in a uniform lossless tube satisfy the following pair of equations
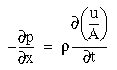
|
(EQ 14) |
|
(EQ 15) |
where p = p(x,t) is the variation in sound pressure in the tube at position x and time t, u = u(x,t) is the variation in volume velocity flow at position x and time t, r is the density of air in the tube, c is the speed of sound, and A = A(x,t) is the cross sectional area of the tube. Rabiner and Schafer [54] show how this equation can be solved to derive the frequency response of the uniform lossless tube, i.e. the ratio of input to output volume velocities as a function of frequency. Figure 34 (A) illustrates this frequency response function, showing periodic peaks corresponding to the poles of the equation, where the response function goes to infinity. These peaks indicate the harmonics of the tube, the lowest one being the fundamental, i.e. the frequency at which one half wave exactly fits in the tube. In an actual physical tube this response function will be somewhat different, as shown in Figure 34 (B), which shows the frequency response function for a uniform tube with yielding walls, friction, and thermal loss. The periodic peaks are still in evidence, although they no longer go to infinity, and the whole function remains within some bounding envelope that diminishes with increasing frequency. The reason why the envelope function decreases with frequency is that the radiation impedance, or resistance to oscillation, increases with higher frequencies. The negative portions of the frequency response in Figure 34 (B) are frequencies at which oscillation is actively suppressed by the harmonic properties of the tube.
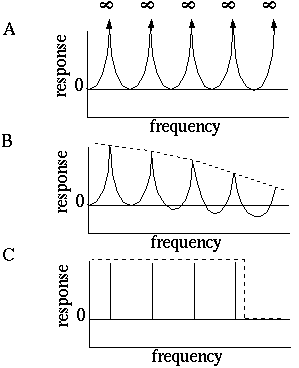
Frequency response of a uniform lossless tube showing harmonic peaks corresponding to the fundamental frequencies (A), and a similar response in a lossy tube where the higher harmonics are suppressed by the impedance of the tube (B). The computer simulations employed the discrete approximation shown in (C).
The principles of harmonic resonance are common to oscillations of sound waves in a resonant cavity, elastic vibrations in a solid object, alternating electric current in an electrical conductor, electromagnetic fields such as a microwave maser or visible light in a laser, and even chemical harmonic resonances in a reaction-diffusion system. In fact, harmonic resonances are a property of all physical systems.
There are several different ways in which harmonic resonances can be supposed to occur in a neural system. Grossberg & Somers [19] show how the oscillatory firing of cortical neurons can be modeled by excitatory and inhibitory interactions between connected neurons in a variety of neural architectures, including the BCS model of cortical visual processing. As an alternative, synchronous firing has also been observed in neurons that are connected by way of gap junctions - specialized synapses which physically connect the cytoplasm of adjacent neurons allowing a direct flow of ionic current between them, producing a direct electrotonic coupling with a transmission speed that is orders of magnitude faster than synaptic transmission. Kandel and Siegelbaum [26] have shown that transmission across electrical synapses is very rapid, and that electrical synapses can cause a group of interconnected cells to fire synchronously. A slight propagation delay between the cells in the syncyctium due either to the transmission delay through the gap, or the natural capacitance and inductance of the neurons, would allow for a phase shift between the synchronously firing cells and thereby establish standing waves of electrical activation consisting of periodically alternating regions of activation and quiescence.
Whatever the exact mechanism responsible for the harmonic resonance, the properties of such resonating systems are mathematically related, and can therefore be modeled independent of the specific implementation involved.
A property of these harmonic resonances is that they are governed only by simple interactions between local elements, and yet these systems are capable of producing a wide array of spatial patterns. The scale of the interaction between vibrating elements, local molecular forces, is much smaller than the size of the emergent waveforms. A principal property of harmonic systems is a tendency to form regular periodic patterns that are integer multiples of some fundamental wavelength, which is determined by the dimensions of the physical system. For example, the harmonic frequencies of a resonant acoustic cavity establish patterns of standing waves that subdivide the cavity into integer numbers of equal intervals, as shown in Figure 35(A).
Acoustical harmonics in a linear tube(A), and a circular tube(B), showing how alternating regions of high and low amplitude oscillations subdivide the cavity into integer numbers of equal intervals. In the linear tube the harmonic pattern is fixed by the boundary conditions at the ends of the tube, while in the circular tube the harmonic patterns can be established at any orientation.
Whereas cavities can be tuned to any fundamental frequency, in the case of an enclosed circular tube, the harmonics subdivide the interval from 0 to 2p into integer multiples of the full circle, as shown in Figure 35 (B), which is no longer an arbitrary measure. While the spatial pattern of nodes is fixed in a linear tube by the boundary conditions at the ends of the tube, in the circular tube a harmonic pattern can occur at any rotation.
I will now present a model of orientational harmonics which performs a Fourier filtering of the orientational signal in the cooperative rosette by way of harmonic resonances in those cells. The effect of this filtering is to complete and regularize any periodicity that is inherent in the activation pattern of the rosette.
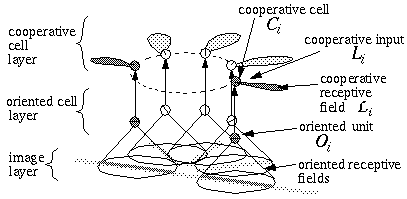
Architecture for orientational harmonic simulation showing a rosette of cooperative cells Ci that receive input from both oriented cells Oi and from cooperative receptive fields Li that receive input from the cooperative layer.
The general architecture for the orientational harmonic model is depicted in Figure 36. A ring of N cooperative cells Ci receive input from N oriented cells Oi from the oriented layer, as well as N inputs from the cooperative receptive field response Li which receive input from regions of the cooperative layer by way of monopolar receptive fields. These receptive fields are defined exactly as in the directed diffusion model Li and Ri, in Equations 12 and 13. The final pattern of activation of the cooperative cell is also influenced by harmonic oscillations within the cooperative rosette, which can be calculated as another input Hi to the cooperative cell. The activation of the cooperative cell is therefore governed by the differential equation
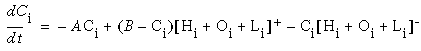
|
(EQ 16) |
The inputs to this equation are Oi, the oriented signal, and Li is the cooperative activation in an adjacent neighborhood as sampled by the cooperative receptive field Li by the equation
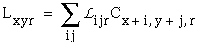
|
(EQ 17) |
The harmonic oscillations within the ring of cooperative cells perform a Fourier filtering of the cooperative signal within the rosette by the filtering function depicted in Figure 34 (B). In the simulations, this function was approximated by a finite comb function with values of unity at the harmonic frequencies, and zeros elsewhere, as shown in Figure 34 (C). A Fourier filtering with this simplified function can be equivalently calculated by convolution with a series of sinusoids Fj with orientational frequency j defined by
|
(EQ 18) |
for filter Fj of the harmonic j of a total of M harmonics, calculated for N values. A zeroeth component filter is also constructed in order to measure the DC component of the orientational signal. The filter for the zeroeth harmonic is defined by
|
(EQ 19) |
where c is a positive constant. These filter profiles look exactly like the waveforms sketched in Figure 32. The filters are convolved with the N cooperative cell values of the N orientations producing a set of response values r given by
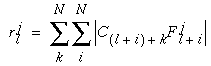
|
(EQ 20) |
for each harmonic coefficient j and for each oriented location i. A total response R is computed for each harmonic by summing over the individual responses at each orientation using the formula
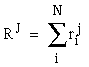
|
(EQ 21) |
The magnitude of this coefficient for each harmonic j represents the magnitude of the response of the system to this harmonic. For example, a large value of R2 would indicate the presence of a strong second harmonic component in the pattern of orientations in the cooperative cells.
So far what has been described is a feedforward process to detect the presence of various orientational harmonics in the cooperative signal, much like a Fourier analysis of that signal. The harmonic resonances in the ring of cells also influence the resultant pattern in those cells by constructive and destructive interference between competing harmonics in the representation. This was calculated by summing the total harmonic contribution Hi of all the various harmonic responses for each cell in the ring of cells, using the formula
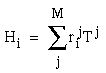
|
(EQ 22) |
where Tj is a top-down priming signal specific to the jth harmonic, which will be explained in detail later. For now, Tj should be considered equal to 1. This harmonic response, together with the oriented input signal Oi and the pattern of activation in adjacent regions of the cooperative layer Li all contribute to the activationa of the cooperative cell Ci , as described in Equation 16. The fact that the input to the cooperative receptive field Li of cell Ci does not receive input from some previous layer, but from within the same cooperative layer represents a recurrent feedback loop within the cooperative layer. On a smaller scale, the activation of the cooperative cell Ci is also influenced by the harmonic interactions between other cooperative cells within the same orientational rosette, corresponding to a smaller, more immediate feedback loop within that structure, although calculated in this case at equilibrium.
In the next few sections I will be analyzing certain specific properties of the orientational harmonic filtering in considerable detail. In later sections I will refer to these detailed phenomena when discussing the more global properties of the harmonic model in more complex situations, where multiple harmonics from different visual features interact in more complex ways.
The effect of orientational harmonics on visual perception is to promote and enhance periodicity in the orientational representation, which corresponds to figural completion by enhancement of regularity. Periodicity can occur at any of several orientational frequencies however, so that the effect of the harmonic processing is not always easy to predict intuitively. A single oriented input, for example, can either be considered as a complete end-stop figure, or as one half of an incomplete straight-through or colinear vertex, or as one third of a three-way vertex, or as one quarter of a four-way vertex, etc. The single oriented input therefore can potentially stimulate any of these harmonics. For example, Figure 37 shows a visual input consisting of a single oriented input at six o'clock, together with plots of the first four harmonics of the orientational frequency, oriented as they would be in response to this single edge input, i.e. with one positive lobe of the periodic response centered at the six o'clock orientation. The first harmonic shows a positive response through the lower half circle (A), the second harmonic shows two peaks at six and twelve o'clock (B), the third harmonic shows three peaks at six, ten, and two o'clock (C), and the fourth harmonic shows four peaks at six, twelve, three and nine o'clock (D). The orientation of these plots correspond to the harmonic response values in Equation 20 for the given input pattern, although the magnitude of each response is modulated by the degree of match between the input pattern and the harmonic pattern. Which of these multiple periodicities should be completed by the harmonic processing? There are two determining factors: first of all, the envelope function of the harmonic response suppresses higher orientational frequencies, which reduces the number of potential completions to a finite number. Secondly, a single edge provides only half of the total input that would define a complete straight-through vertex, and one third of the input for a complete three-way vertex, etc. so that a single edge produces the strongest response in the first harmonic, and the higher harmonics would respond with progressively lesser magnitudes to this particular input. All of these harmonics would however be simultaneously present in the response to this input.
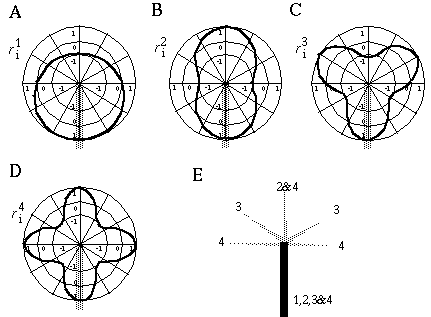
Orientational harmonic responses of the first (A), second (B), third (C) and fourth (D) harmonics of orientational frequency in response to a single vertical edge at six o'clock that terminates at the center of the vertex. These harmonics suggest potential illusory boundary formations in the directions indicated in (E).
Another factor to consider is that different orientational harmonics are more or less compatible with one another, so that a certain measure of `competition' and `cooperation' occurs between the patterns to be completed, although that competition occurs not by way of excitatory and inhibitory interactions between high level nodes in a neural representation, but rather by way of constructive and destructive interference between the waveforms in the orientational rosette. For example, the first harmonic end-stop response to the single edge input at six o'clock shown in Figure 37 (A) produces a negative peak at twelve o'clock, exactly where the second harmonic would produce a positive peak. These two harmonics therefore will tend to cancel one another by destructive interference. Similarly, the second harmonic response produces two negative peaks at three and nine o'clock, exactly where the fourth harmonic would produce positive peaks. The various harmonic responses to the single edge input represent the various potential completions that can be made from that input. Figure 37 (E) shows the locations of all the potential completion peaks of the first four harmonics in response to the single edge input. The actual pattern of illusory boundaries produced by this input would depend not only on the local orientational signal, but also on the influence of orientational signals from adjacent regions, which can "bring out" some of these potential completions while suppressing other competing patterns. For example, a nearby vertical edge in the twelve o'clock direction would promote the second harmonic response, resulting in a vertical grouping percept, as seen in Figure 38 (A). The strength of this response would in turn tend to suppress the fourth harmonic groupings, although all the harmonics would exhibit some response, as shown schematically in Figure 38 (B). The balance of competition between these harmonics can be changed by varying the vertical spacing between adjacent lines, as shown in Figure 38 (C), where the vertical spacing has been increased, although the horizontal spacing remains unchanged. Not only does this weaken the vertical grouping percept, but also, due to the competition between these harmonics, it will strengthen the horizontal grouping percept, even though the horizontal spacing remains unchanged. The third harmonic response can also be enhanced by shifting alternate rows as shown in Figure 38 (E), promoting a percept of a diagonal grouping, as shown in Figure 38 (F). The orientational harmonic theory suggests that all of these groupings are always present simultaneously, and that their relative magnitudes can be varied in analog fashon by adjusting the geometrical arrangement of the inducers.
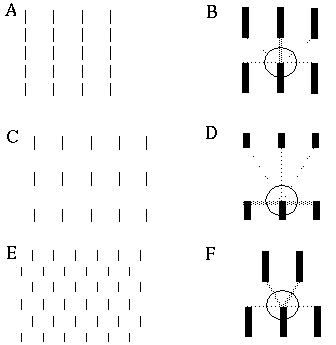
Simultaneous presence of multiple harmonics with different magnitudes is indicated by a vertical alignment as in (A) resulting in a vertical grouping percept due to the second harmonic (B), which can be replaced by a horizontal grouping percept as in (C) by increasing the vertical spacing resulting in a strong fourth harmonic (D), and a diagonal grouping (E) which can be created by promoting the third harmonic response (F).
The situation is more complicated when the original feature at the vertex does not correspond to a simple orientational harmonic, but consists of a more complex form represented by a combination of the fundamental harmonics. For example, Figure 39 shows the response of the first four harmonics to an input consisting of a right angled corner, or "L" vertex. The first harmonic response in Figure 39 (A) produces a positive peak at the bisector of the internal angle between the two edges, because that orientation marks the center of the half-circle which contains the greatest oriented signal. The second harmonic shown in Figure 39 (B) produces absolutely no response to this pattern, since the two input features are separated by 90 degrees,which is exactly the angle between the high and low magnitude lobes of the second harmonic response, so that they cancel exactly, producing no response in this harmonic. The third harmonic forms an optimal alignment with the two lobes aligned approximately with the two edges of the input figure, as shown in Figure 39 (C), leaving a third lobe to bisect the external angle between the two edges. Likewise, the fourth harmonic aligns with two lobes parallel to the two input edges, leaving two additional lobes as linear extensions to the input edges across the center of the vertex, as shown in Figure 39 (D). This analysis shows how the "L" vertex can be represented by a combination of the first, third, and fourth harmonics. The orientational harmonic model would therefore predict potential grouping lines for the "L" vertex in orthogonal and diagonal directions, as indicated in Figure 39 (E), although again, a strong diagonal grouping due to the third harmonic would tend to suppress the orthogonal grouping, and vice versa.
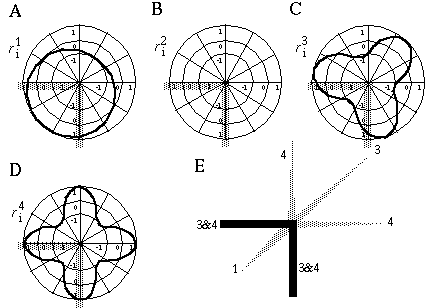
Orientational harmonic responses of the first (A), second (B), third (C) and fourth (D) harmonics of orientational frequency in response to an "L" vertex. These harmonics suggest potential illusory boundary formations in the directions indicated in (E).
An important property of the orientational harmonic system is a large degree of orientational tolerance to angular distortion of the input pattern. The second harmonic, or colinear response, for example, will occur over a wide range of relative orientations, as indicated in Figure 40 (A), where the white segments indicate the range of angles where an input would contribute positively to a horizontal second harmonic pattern, whereas the gray segments indicate regions of negative contribution to that harmonic. For example, the second harmonic would produce a strong response to the vertex pattern depicted by the gray line in Figure 40 (A). The third harmonic however would also produce a strong response to this same pattern, as indicated in Figure 40 (C), although this response would be somewhat diminished due to the absence of an expected input near the twelve o'clock orientation. The second and third harmonic patterns are therefore in competition with one another, and the balance of that competition is greatly influenced by the presence or absence of an input near the twelve o'clock orientation. This means that a second harmonic response can tolerate a range of distortion from colinearity that overlaps well into the range of the third harmonic configuration, so long as there is no input at the twelve o'clock location, as indicated by the range of patterns depicted in Figure 40 (B) all of which would produce a second harmonic response. Conversely, the third harmonic response can tolerate a wide range of distortion so long as there is some input near the twelve o'clock orientation, as shown by the range of orientational combinations depicted in Figure 40 (D). In fact, consideration of the influence of the first and fourth harmonics as well as the second and third restricts the range further, because some of the patterns shown in Figure 40 (B) would produce responses in those other harmonics. For example any of the "V" shaped vertices will produce a first harmonic response due to a uni-lateral asymmetry, and as the angle between the two edges approaches either 90 degrees or 180 degrees, a fourth harmonic response would emerge, generating more positive and negative lobes. Nevertheless, there is considerable flex in the response of these harmonics, and the limits to the distortions tolerated by any harmonic, or harmonic combination, are determined by other harmonics that can better represent that particular pattern due to competition between the different harmonic lobes.
Orientational flex, or tolerance of the harmonic response to distortions of the input pattern due to the wide range of angles covered by the positive lobes of the second harmonic (A) and third harmonic (C) patterns allows these harmonics to respond to a wide range of similar stimuli, as indicated in (B) for the second harmonic, and in (D) for the third harmonic.
A special example of this competition between different harmonic representations corresponds to the conjunctive constraint mentioned earlier, whereby colinear boundary completion is seen to occur only inwards, between visual inducers, not outwards, beyond inducers into featureless space. This can be accounted for in the orientational harmonic model by a competition between the first and second harmonics. A simple example of this phenomenon is seen in Figure 41 (A), where the colinear grouping percept seen connecting the line of dots is not seen to extend beyond the last dots in the line. The orientational harmonic response to a single dot is principally of a circular symmetry, or the zeroeth coefficient of the harmonic series, because a small dot will stimulate an oriented response at all orientations uniformly. A dot that is flanked by other dots in a colinear arrangement would additionally produce a weaker second harmonic or colinear grouping, as shown in Figure 41 (B) and (C) due to input from the cooperative receptive fields from those directions. For the terminal dot at the end of the line however, oriented input from neighboring regions comes exclusively from one side, resulting in a first harmonic or end stop feature, as indicated in Figure 41 (D) and (E). The positive lobe at three o'clock in the second harmonic pattern coincides with the negative lobe at the same location in the first harmonic response, so that these two responses interact by destructive interference. In the absence of an input from the three o'clock orientation this will produce a stronger response in the first harmonic pattern, which in turn will suppress the second harmonic pattern. It must be remembered that the situation is in fact more complex than suggested by the neat diagrams in Figure 41 (B) and (D), because there will actually be some non-zero response to all harmonics, and it is only the relative balance between different harmonics that is different in these two cases. In other words, the second harmonic response is stronger than the first harmonic response in Figure 41 (B), while the first is stronger than the second harmonic in Figure 41 (D).
The conjunctive property shows that illusory boundaries form only inwards between inducers, as seen in (A), but they do not extend outwards beyond the last inducers. This is explained by a competition between a second harmonic response, shown schematically in (B) and (C), with a first harmonic response, shown in (D) and (E), such that the stronger harmonic will suppress the partial response of the weaker harmonic.
Figure 42 shows a computer simulation of the conjunctive constraint. Figure 42 (A) shows the input to the simulation in the form of a line of four dots, and Figure 42 (B) shows the ouput of the orientational harmonic system, showing a strong grouping percept between the dots, with a fainter trail of activation beyond the end of the dots. The activation values along the line defined by the dots is plotted in Figure 42 (E), which shows how the activation decays abruptly beyond the last dots. Long range boundary completion can still occur beyond the last dot despite the action of the first harmonic at the illusory "line ending" due to the subliminal activation due to the second harmonic, which is responsible (in part) for the extended trail of activation beyond the line endings. Figure 42 (C) ) is the same as Figure 42 (A) except that an additional set of four dots are included to the right of the original set, producing a long range interaction as shown in Figure 42 (D). Figure 42 (F) shows the plot of activations along the lines of dots in Figure 42 (D), which reveals how the interaction between the decaying tails of both lines of dots contribute to the activation of the long range illusory boundary between the lines, in much the same way as in the directed diffusion model described in the previous chapter. In the simulations shown in Figure 42, the top-down priming signal T1 in Equation 22 for the first coefficient was boosted to a higher magnitude, 0.5, than those of the other coefficients Tj (for j=0, 2, 3, and 4) which were set to value of 0.25. This is equivalent to a change in the envelope function from the square wave shown in Figure 34 (C), to a closer (but still crude) approximation to the envelope function in Figure 34 (B), which exhibits an greater response to the lower coefficients. The change was made in this simulation to emphasize the effect of the first coefficient.
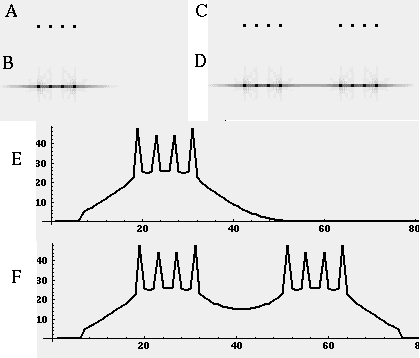
Computer simulation of conjunctive constraint. A line of dots in the input image (A) produces a strong colinear percept (B) between the dots, with a decaying trail of activation beyond the dots. The activation profile is plotted in (D) along the line of dots.
The purpose of the foregoing discussion was to elucidate some of the more subtle interactions between individual orientational harmonics, in order to clarify some of the basic principles of operation of the orientational harmonic model. These interactions can become much more subtle and complicated as all of the harmonics are considered together, and with the introduction of additional spatial irregularities in the input pattern. In the next section I will discuss a variety of different and diverse illusory phenomena that all find an explanation in orientational harmonics. Computer simulations will be used where possible in order to show the exact response predicted by the model for comparison with the psychophysical data.
In the previous section I introduced certain selected perceptual grouping phenomena to illustrate by example different properties of the orientational harmonic model. The most convincing evidence for this model however is not in any single phenomenon that it explains, but rather in the range and diversity of the psychophysical phenomena for which the model can account. In this section I will present a list of these phenomena, with a description of how the model accounts for them, and with computer simulations where necessary to duplicate the perceptual phenomena.
The most straightforward predictions made by the theory concern the illusory boundaries that form between patterns of dots, as shown in Figure 9, because the groupings due to these patterns result exclusively from the global arrangement of the dots, there is no local orientational bias introduced by the dots themselves. Each dot in the pattern stimulates oriented responses at all orientations uniformly, as suggested by the potential grouping lines in Figure 43 (A), so that the formation of illusory boundaries is a result only of the geometrical configuration of the dots themselves, with no orientational bias introduced by the orientational signal at the dots. The model predicts, therefore, that adjacent pairs of dots would tend to form a first harmonic completion, creating an illusory boundary joining those dots, as shown schematically in Figure 43 (B). This explains the pairwise grouping percept shown in Figure 43 (C). As explained in the discussion of the conjunctive constraint above, a second harmonic grouping suppressed by the competing first harmonic grouping, suppressing any completion beyond the two dots.

A small circular dot stimulates all orientations uniformly at that location (A). Interaction between two adjacent dots would boost the first harmonic grouping between them (B) which in turn would suppress the second harmonic grouping, which prevents the illusory boundary from extending beyond the dots. This explains the grouping percept shown in (C).
The orientational harmonic model also predicts a second harmonic grouping to result from a column of nearby dots, as shown schematically in Figure 44 (A), where each dot receives oriented inputs from neighboring dots at six and twelve o'clock, which explains the colinear grouping percept in Figure 44 (B). The second harmonic in turn suppresses a fourth harmonic grouping at the same location, so that the orientational harmonic model predicts that a strong vertical grouping due to close vertical proximity should suppress a weaker horizontal grouping, as suggested in Figure 44 (C). This effect is seen in Figure 44 (D) where a strong vertical grouping is seen, but only a very weak horizontal grouping. The weakness of this horizontal grouping percept is not due solely to the large separation between horizontally adjacent dots, as can be seen in Figure 44 (E), which exhibits a strong horizontal grouping with exactly the same horizontal spacing as in Figure 44 (D), because of the larger vertical spacing which reduces the suppressive effect that the second harmonic can exert on the fourth harmonic grouping. Figure 45 shows a computer simulation of this phenomenon. Figure 45 (A) and (C) show the input to the simulation, and Figure 45 (B) and (D) show the orientational harmonic response to these inputs respectively, illustrating the strong vertical response in (B) and a strong horizontal response in (D). An interesting secondary effect is observed in Figure 45 (B) where the lines defining the periphery of the grid of dots produce stronger boundaries than the internal lines of dots. The reason for this is that the internal lines that terminate at these peripheral lines have a weakened second harmonic response since these internal lines do not continue beyond the boundary, so that the fourth harmonic is disinhibited by this weakened second harmonic response.
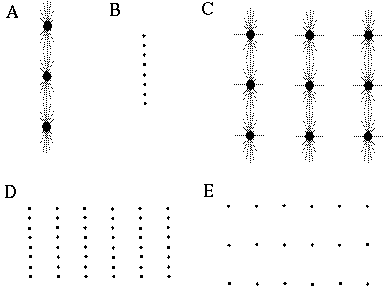
Orientational harmonics predicts a second harmonic grouping for a column of dots (A), which explains the colinear grouping percept seen in (B). The second harmonic grouping is predicted to suppress a fourth harmonic grouping (C), which explains why only a vertical grouping is seen in (D), but the horizontal grouping re-emerges in (E) with an increase in the vertical spacing, although the horizontal spacing of the dots is unchanged.
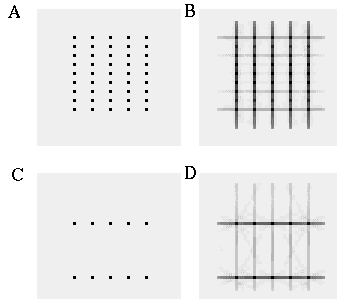
Computer simulation of the vertical grouping percept which suppresses the horizontal percept (A) and (B), and the re-emergence of a horizontal grouping percept when the vertical spacing is increased, (C) and (D).
The orientational harmonic model also predicts a third harmonic grouping between dots that are arranged in a triangular configuration around a central dot, as shown in Figure 46 (A). This can explain the emergent hexagonal grouping seen in Figure 46 (B), where every dot is located at the center of a three-way vertex. Again, orientational harmonics predicts that the neighborhood relations to the nearest dots suppress the pattern defined by more distant dots, which would otherwise contribute to the grouping percept, as suggested in Figure 46 (C). Finally, orientational harmonics predicts a fourth harmonic grouping in a grid of dots where the horizontal and vertical spacing is approximately equal, as suggested in Figure 47 (A), and as seen in Figure 47 (B). Again, a competition would be expected to occur between an orthogonal and a diagonal fourth harmonic grouping, since the diagonal grouping coincides with the negative peaks of the orthogonal grouping. This explains why Figure 47 (B), no diagonal grouping is observed. Figure 47 (C) and (D) show the input and output for the computer simulation of the orientational harmonic response to the equal spaced grid.
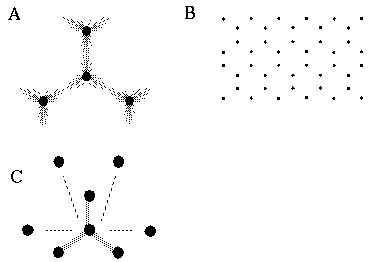
Orientational harmonics predicts a third harmonic grouping to three dots from a central vertex (A), which explains the hexagonal grouping percept (B), where every dot forms such a triangular vertex. This third harmonic suppresses an alternative grouping to more distant dots (C).
Orientational harmonics predicts a fourth harmonic grouping to a grid of dots with equal vertical and horizontal spacing (A), which suppresses a diagonal grouping to dots that are just a little more distant. This explains the grid-like grouping percept in (B). The input and output of the computer simulation of the fourth harmonic grouping is shown in (C) and (D) respectively.
The tolerance to orientational distortion that was mentioned as a property of the orientational harmonic system would predict that considerable distortion could be applied to a pattern of dots without significantly altering the orientational harmonic response, as suggested in Figure 40. For example, a second harmonic grouping would be expected for a line of dots that defines a curve, through a range of different curvatures, as shown in Figure 48 (A). At a certain critical curvature the line appears to "kink" into a sharp vertex. This kinking occurs at approximately that curvature where the magnitude of the second harmonic begins to be exceeded by the magnitude of the third harmonic, as shown in Figure 48 (B). This property is consistent with the perceptual data of Wilson and Richards [69] which show that the perceptual acuity to curvature discrimination increases quite suddenly at about that same curvature. It is also consistent with the observation by Kanizsa [28] who shows that circles of dots generate a circular grouping percept at low curvature, but break into a polygonal percept as the curvature exceeds a certain value. This phenomenon is illustrated in Figure 48 (C).
Orientational harmonics predicts that a second harmonic grouping will tolerate a large degree of distortion (A) until the angle of the vertex exceeds the angle where the third harmonic response is greater than the second harmonic response (B), at which point the percept breaks into a sharp vertex. This also explains why a circle of dots begins to appear as a polygon (C) when the curvature of the illusory boundary exceeds about the same critical angle as depicted in (B).
The tolerance to orientational distortion applies just as well to third harmonic groupings as to colinear groupings, as discussed in the previous section. Orientational harmonics would therefore predict that a pattern of dots defining a three-way vertex could experience considerable distortion while still maintaining a triangular percept, as shown in Figure 49 (A). In fact, the triangular percept only breaks down when the pattern begins to resemble a "T" vertex more than the triangular one. There is no point between these two extremes where the pattern appears as neither a "T" nor a triangular vertex. This tolerance to distortion may account for the fact that constellations of stars are seen as a pattern of lines that connect the individual stars, as shown in Figure 49 (B). The recognition of a familiar constellation depends not so much on the exact geometrical arrangement of the stars, but more on the pattern of vertices defined by those stars. The constellation in Figure 49 (C) for example is geometrically quite different from the one in Figure 49 (A), as the relative locations of all of the stars have been shifted. Nevertheless, this pattern is still readily recognizable as the big dipper, because it is defined by the same combination of harmonic vertices, although each vertex is distorted to different angles. The patterns in Figure 49 (D) and (E) on the other hand are geometrically much more similar to that in Figure 49 (A): in each case only one star has been shifted, but these patterns appear much less similar to the original because they are no longer composed of the same combination of vettex types. In Figure 49 (D) for instance the central star was shifted to change the triangular vertex to a "T" vertex, while in Figure 49 (E) the star at the lower right was shifted to change the "L" vertex to a colinear one.
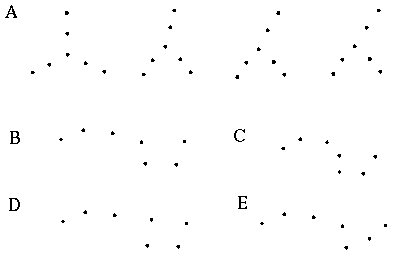
Orientational harmonics predicts that the third harmonic grouping will survive considerable distortion (A) until the grouping begins to resemble a different vertex type. This same transition between vertex types is pivotal in visual recognition of constellations (B), which remain familiar even when distorted geometrically, as long as their constituent vertex types remain unchanged (C). A much lesser geometrical distortion, due to shifting only a single star, (D) and (E), can disrupt the recognition if it changes a basic vertex type, as defined by orientational harmonics.
In the grouping percepts presented above, the oriented inducers consist of dots, whose circular symmetry ensures that the influence on the orientational harmonics comes exclusively from the relative positions of the dots, there being no orientational bias introduced by the orientational signal at the dots. In many circumstances however, there will be a local oriented signal that contributes an orientational bias to the global grouping percept. Consider the case of an oriented inducer that stimulates only a single orientation at a particular spatial location. That oriented signal in turn stimulates a field of oriented activation at adjacent locations and nearby orientations, which promotes boundary completion in a manner similar to the directed diffusion model described in Chapter Two. Figure 50 (A) illustrates this kind of boundary completion between two nearby oriented signals producing a colinear grouping percept between them.
It should be noted that as in the case of the directed diffusion model, this kind of boundary completion can occur over distances that are greater than the gap spanned by a pair of cooperative receptive fields in the "rosette", as shown in Figure 50 (B), where a central cooperative unit is set into second harmonic mode by two nearby oriented inputs, producing a colinear completion. Figure 50 (C) shows how this diffusion of oriented signal can propagate still farther by virtue of the fact that an oriented input generates a response in all of the harmonics simultaneously, even though the magnitudes of some harmonics will be stronger than others. In the figure, the rosettes which are adjacent to the two inducers initially receive input from one direction only, resulting in a predominantly first harmonic response. A weaker second harmonic response will also be stimulated by this input however, allowing a weak signal to propagate to a central rosette from both directions. The resulting second harmonic response in the central rosette will promote second harmonic patterns in the neighboring rosettes, and the resulting pooling of activation will complete the entire boundary.
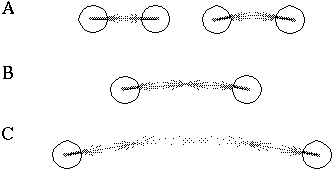
Boundary completion between oriented inducers occurs in a manner similar to the directed diffusion model, either by local interactions between adjacent rosettes (A), or by a more distant interaction through intervening rosettes (B) and (C).
The nature of the oriented filtering with oriented receptive fields is such that oriented signals consisting of only a single orientation will never arise, because oriented edge detectors have a finite orientational resolution, so that even a visual input consisting of a single orientated edge will always register partial responses in adjacent orientations. Furthermore, a line ending generates additional oriented signals due to the fact that, like a small circular dot, the line ending stimulates a range of different orientations, although there will be a strong bias in a direction parallel to the orientation of the line, as suggested in Figure 51 (A). The exact distribution of orientations will depend on the size and geometrical configuraion of the oriented receptive field, as well as on the exact shape of the line ending. Like the small circular dot therefore, the line ending can participate in virtually any grouping configuration, depending on the proximity of similar orientations. The orientational harmonic theory predicts an enhancement of the orientational periodicity of this signal at each vertex due to the local orientations present at that vertex, as well as with the global grouping due to neighboring oriented features. For example, given an additional input at twelve o'clock, the harmonics would selectively amplify those orientations in Figure 51 (A) that are consistent with a second harmonic interaction or colinear grouping producing the more orientational periodic percept as shown in Figure 51 (B) with a vertical harmonic response and a weaker third and fourth harmonic response at each vertex. These additional harmonics remain weak because they have no features with which to complete globally. Given a regular array of such lines however, harmonic interactions can produce a more regular percept, with potential groupings for all of the harmonics, as shown schematically in Figure 52. These interacting harmonic lines form a regular grid or lattice between the oriented features corresponding to the various harmonics present in the image. Figure 52 (A), (B), and (C) show how the precise spatial arrangement of the array of short oriented line segments produces different sets of grouping percepts. This is explained in the orientational harmonic model by the fact that different grouping arrangements favor different harmonics selectively, and that competition between harmonics accounts for the emergence and disappearance of different components of the grouping pattern. For example, the close vertical proximity of the lines in Figure 52 (A) supports a second harmonic grouping as shown in Figure 52 (B), which in turn suppresses the fourth harmonic horizontal grouping. That grouping, as well as a diagonal third harmonic grouping are still present, but with much diminished magnitude. The closer horizontal spacing in Figure 52 (C) promotes a fourth harmonic grouping, as shown schematically in Figure 52 (D). Again, all harmonics remain present, but the strength of the fourth harmonic suppresses the second harmonic vertical grouping percept. Figure 52 (E) shows how a diagonal grouping can be brought out by a diagonal alignment of the oriented line segments, which is explained schematically in Figure 52 (F). This percept will be naturally weaker because it does not make use of the strong vertical component inherent in the vertical line segments. Figure 53 shows the results of computer simulations of these phenomena, where Figure 53 (A), (C), and (E) show the inputs to the simulation, while 53 (B), (D), and (F) show the corresponding outputs respectively. Notice how in each case, all harmonics are in evidence, but that different arrangements favor particular harmonics, which accounts for the resulting perceptual grouping.

Distribution of orientational response at a line ending (A), showing how global groupings between line endings would selectively enhance common orientations between nearby line ends (B). The additional influence of orientational harmonics is not depicted here.
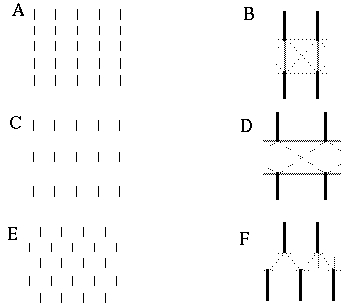
A close vertical proximity between the oriented line segments (A) promotes a vertical second harmonic grouping (B); a close horizontal proximity (C) promotes horizontal fourth harmonic grouping (D); a close diagonal proximity (E) promotes diagonal grouping (F).
Computer simulations of the three grouping percepts seen in arrays of short vertical lines. The simulation input is shown in (A), (C), and (E), and their corresponding outputs are shown in (B), (D), and (F) respectively.
I have shown how the influence of the local orientational bias inherent in an oriented line ending contributes to the overall balance of harmonic grouping forces at the vertex. I have also shown in Figure 39 how the orientational harmonics at an "L" vertex interact locally producing a characteristic pattern of orthogonal and diagonal potential grouping lines from that feature. Orientational harmonics therefore predicts that a square, which is composed of four such "L" vertices will posses similar orthogonal and diagonal potential grouping lines, as illustrated in Figure 54 (A), and that these two groupings will compete with each other, so that a strong percept of one would suppress the perception of the other. This suggests that squares will tend to group well orthogonally, as in Figure 54 (B), or diagonally, as in Figure 54 (C), but not both simultaneously. Figure 54 (D) and (E) show the input and output of a computer simulation showing the orthogonal grouping percept, while Figure 54 (F) and (G) show a computer simulation of the diagonal grouping effect. Notice that in Figure 54 (G) the actual grouping should occur at an angle of 45 degrees, which was not represented in the computer simulation due to orientational quantization, so the grouping percept is seen instead in the nearest represented orientations at 30 and 60 degrees.

Potential grouping edges predicted for a single square by orientational harmonics (A) predicts orthogonal (B) and diagonal (C) groupings between squares. Computer simulation inputs (D) and (F), and output (E) and (G), showing orthogonal and diagonal groupings between squares.
The tolerance to orientational distortion of the orientational harmonic system would dictate that "L" vertices that deviate from perfect right angles would nevertheless posses similar potential grouping lines as the perfect right angle. Specifically, orientational harmonics predict edge projection and corner projection potential grouping lines for the "V" vertex, as shown in Figure 55 (B), which correspond to the orthogonal and diagonal grouping lines respectively, seen in the right angled vertex in Figure 55 (A). As in the case of the right angled vertex, the edge projection and corner projection lines compete with each other, so that a strong percept of one will tend to suppress the perception of the other. Orientational harmonic theory predicts therefore that a triangle will project potential grouping lines from its corners as indicated in Figure 55 (C). Furthermore, the theory predicts that a strong grouping percept will result from any geometrical arrangement of triangles where some set of these grouping lines from different triangles coincide. Furthermore, the theory predicts that a strong edge projection grouping will suppress a corner projection grouping percept, and vice-versa. These simple predictions will be seen to explain a large number of grouping percepts.
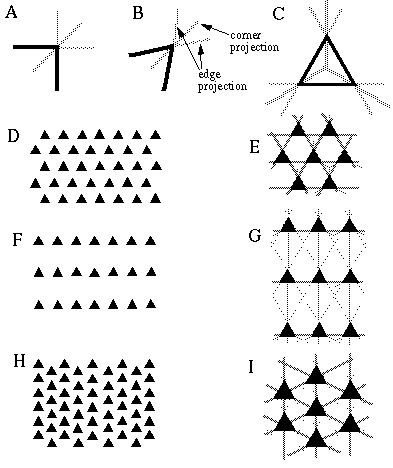
For example, Figure 55 (D) shows an arrangement of equilateral triangles such that adjacent edges are colinear. Not surprisingly, a strong grouping percept is seen in the form of parallel lines in three orientations, parallel to the three edges of the triangles. It is also noteworthy that a vertical grouping is not readily seen, despite the fact that alternate rows of triangles are vertically aligned. Figure 55 (E) shows the orientational harmonic explanation for this phenomenon, where the strong edge projection groupings are seen to suppress the corner projection grouping lines at orientations of zero, 135, and 225 degrees.
Removal of the alternate rows of triangles in Figure 55 (F) induces a vertical grouping percept to some degree, although the predominant grouping now is horizontal, due to the alignment of the edge projection lines from the base of the triangles. The other edge projection groupings corresponding to the other two sides of the triangle are considerably weakened however, which can be explained by a competition at the top vertex of each triangle between the vertical corner projection grouping and the two edge projection groupings at that same corner. Figure 55 (G) shows the lattice of intersecting grouping lines predicted by orientational harmonics.
Alignment of the triangles by way of their corner projection lines results in the pattern shown in Figure 55 (H), where groupings can be seen either at vertical, 135 degree, or 225 degree orientations, corresponding to the three corner projection orientations. Again, the edge projection lines, which are otherwise perfectly aligned for alternate triangles, are greatly suppressed by competition with the strong corner projection grouping. This can be seen in the orientational harmonic explanation shown in Figure 55 (I). Note also the contrast between the grouping patterns of Figure 55 (D) and (H), where the former creates a single, stable grouping percept, while the latter reveals a more rivalrous grouping, where the percept alternates between the three principal orientations. Orientational harmonics has an explanation for this phenomenon in that an edge projection grouping passes through the triangle in a straight line, as shown in Figure 56 (A), whereas the corner projection grouping forks in the center of the triangle, as shown in Figure 56 (B). This means that an array of triangles can be arranged to share their edge grouping lines, as shown in Figure 56 (C), whereas this is impossible by way of the corner projection lines, as shown in Figure 56 (D).
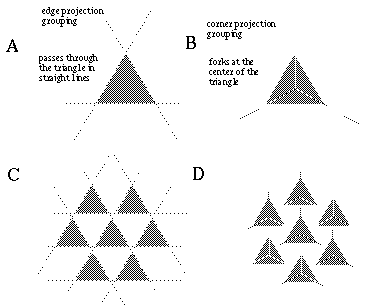
The edge projection grouping (A) passes through the triangle in straight lines, while the corner projection grouping (B) forks at the center of the triangle. This means that an array of triangles can be aligned along their common edge projection lines (C), but the corner projection lines are in conflict with each other (D).
The orientational harmonic model predicts the various alternate percepts seen in the minimal Ehrenstein figure shown in Figure 57 (A). A fourth harmonic grouping at the four line endings generates orthogonal end cuts to the inducing lines, which are then further completed either by second harmonic completion creating the illusory circle percept, or by fourth harmonic orthogonal completion creating the square percept. Alternatively, a third harmonic grouping at the line ending creates diagonal completion to the other line endings resulting in the diamond percept. These different harmonic interactions are depicted in Figure 57 (B), and a computer simulation is shown in Figure 57 (C) and (D).
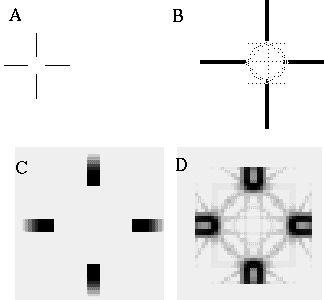
The minimal Ehrenstein figure (A), and the orientational harmonic explanation for the three alternate possible percepts (B). A computer simulation (C) and (D) exhibit the same grouping properties.
The orientational harmonic theory provides a mechanism that can perform boundary completion through any combination of orientations that meet at a vertex. In the process, harmonic interactions between these oriented signals will result in an enhancement of some patterns and a suppression of others. The nature of these interactions however is consistent with the observed psychophysical interactions between illusory groupings due to visual inducers, which gives this model a good deal of explanatory power for such illusory phenomena. Furthermore, the mechanism of orientational harmonics is a simple harmonic resonance within the orientational representation, requiring no complex architectural components.
The representation of orientational combinations in the orientational
harmonic system is expressed in terms of periodicity in the
orientational signal, corresponding to regularity in the visual
world. I will show in the next chapter that this property of the
system provides an opportunity for a compression of the visual
information consistent with Attneave's discussion of information
theory, resulting in a highly compressed and invariant
representation.
By the principles of information theory, as discussed by Attneave, a
primary function of the visual system is to encode visual information
in a more compact representation for the purposes of recognition and
recall. The system I have described so far performs very little
abstraction, representing instead a veridical facsimile or internal
copy of the visual world. Furthermore, this representation requires
the continued presence of the visual input in order to maintain the
patterns of activation in the system. A higher level representation
would have to extract significant features from this representation
and to encode them in a compact form. The purpose of this compact
representation would be for recognition and recall, so that the
abstract representation must be able to be matched to a visual input,
where a measure of the match can be made. Another desirable property
for such a system would be a certain measure of invariance in the
representation, so that a single "template" can be used to recognize
the multiple possible rotations, translations, and scales of
different patterns.
I have indicated that the points of high curvature, or vertices of an
image have been shown to contain more perceptual information than the
lines that join them. It would be natural for a higher level representation scheme to encode individual vertices and combinations of
vertices in the high level representation. When it is time for recall
or matching, the top-down generation of these vertices in the visual
field will stimulate boundary completion between them, ready for a
point by point matching with the visual input. This principle is
suggested in Figure 58: at (A) is an image of a solid triangle; (B)
depicts the oriented signal for that input, where shading represents
an oriented signal of any orientation; (C) depicts the response of the
bipole cell of the BCS, or the second harmonic of orientational
frequency, which would respond only along continuous boundaries; (D)
depicts the locations where higher order harmonics are found. Although
the higher order harmonics arise in response to such vertices, there
is no cell in the system that is active in the presence of these
vertices and inactive in the absence of the vertices. How could the
orientational harmonic system be used to yield a compact
representation for learning and recognition?
Schematic illustration of the levels of encoding of a visual form; (A)
image of triangle, (B) oriented signal, (C) colinear signal, (D)
higher level representation.
The spatial pattern of acoustical harmonics in a resonant cavity is
related to the temporal frequency, or tone produced by that
harmonic. For example, the fourth spatial harmonic will have a
temporal frequency that is double that of the second spatial
harmonic. In a linear tube, the spatial pattern is fixed in relation
to that tube, but in a circular tube that spatial harmonic pattern can
occur at any orientation. The temporal frequency or tone on the other
hand remains constant across different rotations of the spatial
pattern, but is characteristic of the orientational frequency of that
pattern. Temporal frequency therefore is a rotation invariant
representation of the orientational harmonic pattern, and can be used
both bottom-up, to identify orientational harmonics, or top-down, to
prime or boost specific harmonics. Figure 59 illustrates this
principle in a physical analog. Figure 59 (A) depicts a closed
circular tube which is stimulated at certain points by white noise
generators, like the mouthpiece of a flute, and muted at other points,
as indicated by the holes in the tube which, like the holes in a
flute, locally quench the oscillations, thus stimulating the formation
of nodes. This is analogous to a ring of neural tissue receiving
excitatory and inhibitory input, resulting in a spatial pattern of
activation. In the example of Figure 59 the pattern corresponds to
bilateral symmetry, with two horizontal excitatory inputs. Although
the spatial pattern of the second harmonic oscillation can normally
occur at any orientation in the tube, the fixed location of the
excitatory and inhibitory inputs constrains the pattern in this case
to a horizontal orientation. The temporal frequency of this
orientational harmonic however is invariant to rotation. A bank of
sensors tuned to the temporal frequencies of the orientational
harmonics therefore would detect the presence of their own harmonic in
the input regardless of the absolute orientation. Furthermore, a bank
of oscillators tuned to the same frequencies could stimulate periodic
activity in the resonant tube at any orientation, the actual
orientation chosen would either be completely random, or would be
influenced by any bias introduced by the input.
Acoustic analogy for high-level representation of orientational
harmonics. The oriented signal is represented by a white noise input
applied at particular locations to a closed circular cavity, resulting
in second harmonic oscillation (A). Top-down reconstruction of the
same second harmonic pattern can be achieved by stimulating the cavity
with the second harmonic frequency (B), which re-establishes the
second harmonic standing wave.
The next set of simulations illustrate these principles. In these
simulations the harmonics of the system are investigated at a single
location in the system, as in the experiments of the previous
chapter. Figure 60 shows the results of these simulations. The thick
radial lines extending outwards from the inner circle plot the input
pattern Oi, while shaded region plots the
equilibrium value of the cooperative cells Ci, as in
Equation 8, quantized into twelve orientations, as indicated by the
thin radial lines. The bar charts to the right of the dials depict the
harmonic content of the bottom-up input . This response represents the
bank of tuned filters that detect the temporal oscillations
corresponding to the orientational harmonics. Additional bars are
displayed to the right, that represent the top-down prime,
corresponding to the tuned oscillators that can stimulate particular
harmonics in the system. These correspond to the "envelope function"
Tj mentioned earlier, but in this simulation they
can be set interactively with the mouse during the simulation.
Computer simulation of rotation invariance of the bottom-up harmonic
signal. The oriented input pattern, represented by the thick radial
lines, stimulates a pattern of harmonic activation in the cooperative
cells, represented by the shaded region. The same pattern is presented
in both (A) and (B) but at different rotations. The bottom-up harmonic
response, indicated by the bar charts, shows no change during the
rotation.
The first simulation depicted in Figure 60 (A) shows the response
of the system to a crude tri-lateral pattern, exhibiting the
regularization properties discussed in the previous chapter. The
response of the system indicates a third harmonic pattern, as
indicated by the strength in the R3 signal. The
rotation invariance of this representation is shown in (B), which is
the same pattern rotated clockwise by 60 degrees, without any change
seen in the harmonic response pattern. Figure 61 (A) shows the response of the system to an ambiguous
input pattern, chosen to stimulate both the second and third harmonic
responses, although the second harmonic records a somewhat closer
match to this pattern, as seen by the somewhat stronger value of
R2. The top-down prime was then progressively
adjusted by increasing T3 while reducing
T2 until the configuration of primes depicted In
Figure 61 (B) was achieved. All the while, virtually no change was
observed in the pattern of activation in the cooperative ring except a
slight reduction in cooperative cell activity at the twelve and five
o'clock orientations, together with a slight increase in activity at
the ten and seven o'clock positions. A critical transition was seen to
occur at the configuration of top-down priming values shown in Figure
61 (B), when suddenly a bud of activation was seen to appear at the
two and three o'clock positions, followed by a rapid reconfiguration
of the activation patterns in the cooperative representation,
accompanied by a radical change in the bottom-up harmonic
representations. The equilibrium values for the cooperative pattern
and the harmonic response are shown in Figure 61 (B).
Computer simulation of top-down priming. An ambiguous input pattern,
indicated by the thick radial lines is presented, producing a pattern
of cooperative activation, indicated by the shaded region. The
bottom-up harmonics indicate a predominantly second harmonic pattern,
but with a strong third harmonic component. The top-down priming
signal was then progressively modified to enhance the third harmonic
while suppressing the second harmonic. At a critical point, the
bottom-up third harmonic suddenly grew while the second harmonic
decayed, and at the same time a third harmonic pattern of activation
was seen to appear in the cooperative representation, "halucinating" a
third branch to the input pattern.
This model raises several interesting issues of relevance to visual
perception and representation. In many visual models, features are
extracted from the input by specialized feature detectors, the
response to each feature being represented by the activation of the
corresponding node. In models that involve competition or
cooperation between features, that interaction is often implemented by
lateral inhibition or excitation between these higher level nodes. The
system proposed here is fundamentally different in the sense that what
competition or cooperation exists in the model, occurs not by way of
explicit interactions between high level representations, but rather
occurs node by node at the lower level of representation by way of
constructive and destructive interference between competing waveforms
in a distributed representation. Indeed, that interaction between
competing representations occurs independent of the higher level
representation, as was seen in the previous chapter, and can be seen
as a low level consistency matching at the highest possible resolution
in the system between alternative representations of the input signal.
The manner in which the top-down priming influences perception in
the system is also noteworthy. In the simulation depicted in Figure 61
(A) and (B), the ambiguous input pattern stimulated both the second
and the third orientational harmonics, leading to an activation of the
R2 and R3 nodes in the system. In
a purely feedforward system, this higher level abstraction of the
lower level pattern would be the only information available to a
recognition or decision process. But the dimensionality of this
abstraction, one value for each harmonic coefficient, is far more
impoverished or compressed than the intricate balance of competing
waveforms in the lower level cooperative representation. Indeed the
interactions between the multiple waveforms present in that
representation is not reducible to a single dimension without a great
loss of resolution. During the dynamic simulation shown in (B), when
the top-down bias favoring the third harmonic is first applied, the
interactions between waveforms in the cooperative representation
slowly bends the activations of the two branches of the bilateral
pattern against their natural tendency to remain colinear, in an
attempt to make room for a third branch, even though the bottom-up
signal R2 still dominates the third harmonic
R3. A sudden change is seen to occur as soon as an
illusory third branch sprouts, after which the system quickly
re-equilibrates to a third harmonic condition as the third branch
grows in size and the bottom-up feature representation reflects a
predominantly third harmonic pattern. In this system therefore, the priming of the T3
node initiates a fundamental shift in the balance of forces at the
lower level cooperative representation, causing the pattern there to
bend as if under stress, as the third harmonic attempts to establish a
third branch of activation. The success of this priming on changing
the final percept depends intimately on the context at the lower
level, whether the rest of the inputs at that location, and at
neighboring locations in a full simulation, are also consistent with
this new trilateral pattern. In a full simulation complete with
neighboring units and oriented input, the bending of the two arms of
the bilateral pattern would subtly shift the forces in all the
neighboring cooperative units, resulting in a different dynamic
balance of forces throughout the cooperative layer. This new balance
of forces could either promote the growth of the third branch (by
increasing the activation at the two and three o'clock orientations),
or inhibit it, in a way that would be impossible to predict by
analysis of the high level representation alone. The manner of
operation of the top down priming in this system therefore is not in
the form of an "intellectual" competition between the high level
abstractions represented by the R2 and
R3 nodes, but rather, the competition is more of a
"physical" struggle between the low level embodiments of these high
level nodes, in the context of the lattice of interacting forces in
the cooperative layer. The top level nodes communicate the urgency,
and monitor the outcome of the competition between representations,
but the competition itself takes place at the lowest level between the
waveforms themselves.The close coupling between adjacent nodes in this
system produces an intricate network of interacting forces. Simple
priming of a single node therefore results in a shift in the balance
of the entire representation. In this sense, the top down priming is a
highly context sensitive operation. This principle is seen in the orientational harmonic response to
the minimal Ehrenstein figure. As was mentioned previously, this
figure rests at a saddle point in perceptual space, and can be seen as
one of three different percepts, as illustrated in Figure 8. Coren
et al. [7] show that top-down priming can
influence the probability of perceiving this figure as one or another
of the several possible forms illustrated in Figure 8. Figure 62 (A)
shows the input used to simulate the Ehrenstein figure, while Figure
62 (B), (C), and (D) show the orientational harmonic responses to this
figure with additional top-down priming given to the
T2, T3, and T4
harmonics respectively, boosting their value from the default of 0.5
to a primed value of 2.0. The priming in this simulation is applied
uniformly to the entire image, non-specific to either spatial
location, nor to orientation. The effects of the priming however have
very specific spatial and orientational effects, depending on the
context in the image. Those features that are consistent with the
primed harmonic will respond to the prime at the location of that
feature and at the specific orientation where that harmonic fits
best. This is an important property of priming in this system, and has
relevance to the issue of priming in human perception, illustrating
how a nonspecific prime can enhance a specific pattern given the right
kind of invariant representation in the system.
Effect of top-down priming on the orientational harmonic response to
the minimal Ehrenstein figure (A). to bring out the illusory circle
(B) by second harmonic priming, the diamond (C) by third harmonic
priming, and the square (D) by fourth harmonic priming.
In Figure 62 (B) for example, it is the second harmonic,
T2, which is boosted, which emphasizes the
colinearity, or resistance to kinking of the illusory boundary. This
results in a pattern consistent with the circular Ehrenstein figure,
corresponding to Figure 8 (C). This response should be compared to the
unprimed response illustrated in Figure 57 (D). Note that in this
simulation, the "circle" in the middle is actually a dodecahedron,
because of the quantization in the simulation to twelve
orientations. Figure 62 (C) shows the result of priming with the third
harmonic. It is this harmonic that is responsible for the diagonal
lines extending from the corners of rectangular features, so a strong
prime of this orientational frequency will stimulate a percept of the
diamond shape in the minimal Ehrenstein figure. This diagonal response
is less crisp and clear than the circle and square shapes in Figure 62
(B) and (D) because of orientational quantization, i.e. the 45 degree
direction was not represented explicitly in the simulations because
the circle was quantized at 30 degree intervals, so the diagonal
responses in Figure 62 (C) were represented by the adjacent 30 and 60
degree orientations instead, resulting in a more diffuse illusory
boundary. Figure 62 (D) shows the orientational harmonic response with
a priming of the fourth harmonic. This boosts the right angle vertices
of the figure, resulting in strong corner responses to the square
perceptual figure, as well as bringing out orthogonal intersections
throughout the image. The simulation results shown in Figure 62 were
normalized to the maximal activation in order to bring out the weaker
responses, which explains why the non-illusory boundaries of the
inducers appear much stronger in Figure 62 (C), where much boosting
was required, than in Figure 62 (B) and (D). These simulations illustrate the interaction between the top-down
priming and the bottom-up input in this model. The top-down priming
favors a particular lower level pattern. If that pattern is consistent
with conditions at the lower level, then the priming will succeed in
reinforcing that pattern over competing patterns at the lower
level. As that pattern grows in strength, it in turn feeds activation
back up to its higher level abstraction, thus closing the feedback
loop. This close coupling between the bottom-up and top- down
representation in this system is reminiscent of the Adaptive Resonance
Theory (ART) of Carpenter and Grossberg [ 5]. In
the ART model, as in the orientational harmonic model, bottom-up and
top-down representations collide in the lower representational layer,
leading to constructive and destructive interference between the low
level embodiments of the alternative high level patterns in that
layer. The principal difference in this model is that competition
between alternative higher level representations occurs implicitly at
the lower level by waveform interference, rather than explicitly, by
lateral inhibition between the higher level nodes. There has been much discussion in the literature of late on the
observation by Eckhorn et al. [9] that
boundaries that are part of a larger global boundary stimulate
cortical cells to fire synchronously in single cell recordings. This
has led to speculations that the phase of neural firing must be used
by the brain to encode or label the identity of those features, or to
segment them into wholes. The orientational harmonic model suggests
that such synchronous firing might be an artifact of the tight
harmonic coupling that occurs in the oriented
representation. Furthermore, this model makes the specific prediction
that the temporal frequency of spiking of such cells will depend on
the orientational harmonics of the input pattern, so that, for
example, the frequency of spiking to a cross shaped stimulus will be
double that for a single bar stimulus. As I mentioned in an earlier section, the orientational harmonics
can be considered to be a measure of the symmetry of the pattern at
each level. The notion of symmetry has always held a particular
significance in Gestalt psychology, which recognized symmetry as an
example of "Prägnanz", or "goodness" of Gestalt, which Palmer [47] defines as greater simplicity, order, or
regularity. Garner [14] reports that subjects can
remember figures with "good Gestalt" better, can match them more
quickly, can describe them in fewer words, and can learn them more
quickly. All this suggests that symmetry plays an important role in
visual perception. Garner [14] describes a
perceptual experiment where the "goodness" of certain patterns is
measured psychophysically, by measuring how easily they are learned or
recognized. Garner notes that the psychophysical results correspond to
a mathematical symmetry measure, whereby figures are quantified to the
extent that they are the same as transformed versions of themselves,
where the transformations are 90 degree rotations, and reflections
about the vertical, horizontal, and diagonal axes. The number of
distinct patterns that can be achieved by these rotations and
reflections constitutes the pattern's Rotation and Reflection (R & R)
subset. Figure 63 illustrates this point with five figures used by
Garner, composed of patterns of dots. Any of the allowable rotations
and reflections on pattern (A) in Figure 63 result in a pattern
identical to (A), in other words, there is only one pattern in the R &
R subset of pattern (A). For the patterns (B) through (D) of Figure 63
on the other hand, the size of the R & R subset is four, i.e. each of
these patterns can be transformed into four distinct patterns by one
or more of the allowable rotations or reflections. Pattern (E) in
Figure 63 has eight distinct patterns in its R & R subset, indicating
even more asymmetry in this pattern. Garner shows that there is a
direct correspondence between the number of a pattern's R & R subset,
and that pattern's Gestalt "goodness" as measured psychophysically,
i.e. he shows that pattern (A) has more Gestalt "goodness" than
patterns (B), (C), and (D), which in turn have more "goodness" than
pattern (E) in Figure 63.
Rotation and reflection subsets for five example patterns. The number
below each pattern indicates the number of distinct figures that can
be generated by various combinations of rotations and reflections of
the original figure.
One property of the orientational harmonic representation is that the
orientational frequency response of a pattern remains unchanged over
any of the R & R transformations. In other words, the orientational
harmonic system cannot distinguish between two patterns that are R & R
transformations of each other. A pattern like (A) in Figure 63 could
therefore be represented compactly in an orientational harmonic system simply by its orientational frequency response, whereas a pattern
like (B) in Figure 63 would need additional rotation variant
information in order not to be confused with the three other patterns
in its R & R subset, from which pattern (B) must be
distinguished. This provides another piece of evidence in favor of the
orientational harmonic theory for human pattern recognition because
the orientational harmonic representation, like human perception, can
represent a pattern most compactly if it is invariant across R & R
transformations, and requires additional rotation variant information
to distinguish between the members of a pattern's R & R subset.
The orientational frequency model makes several interesting statements
about the nature of visual processing in the brain. The principal
message behind this model is that complex global properties are seen
to emerge from simple local interactions. This is a common theme seen
throughout the work of Stephen Grossberg over two decades of neural
modeling. It is also the message of the Gestalt movement, that has
always favored simple dynamic mechanisms as models of visual
perception. A simple perceptual mechanism does not imply simple
percepts, as can be seen in the complex harmonic patterns that emerge
from simple molecular interactions in a resonant cavity.
The harmonic properties addressed by this model are just the tip
of the iceberg of possible harmonic patterns that can arise through
oscillations in a homogeneous medium. The truth of this statement can
be seen in the complex array of resonant patterns that arise in the
Chladni figures [ 6] which are induced in uniform
steel plates by bowing the plate with a violin bow. The resulting
pattern can be visualized by sprinkling sand on the plate, which tends
to collect at the oscillatory nodes, thus revealing the harmonic
patterns in the plate. Figure 64 illustrates just some of the patterns
that can arise in this manner. Certain characteristic properties are
seen in such patterns, such as symmetry and periodicity, in radial,
circumferential and rectilinear dimensions. I believe that it is no
accident that the properties of symmetry and periodicity are also
fundamental to the Gestalt laws of perceptual grouping. If such
complex patterns are seen to arise from simple homogeneous media such
as resonant tubes and steel plates, one can only begin to imagine the
kinds of patterns which might arise from more complex resonant
harmonic structures such as the visual cortex.
Chladni's Figures which are generated by vibrations in a circular
steel plate which indicate some of the many modes of oscillation
possible in this simple system.
Some hints can be seen in a diverse literature of seemingly
unrelated material. Work on reaction diffusion [
66, 42] in biological morphogenesis [62] reveals a chemical harmonic resonance that has
been shown to be responsible for the establishment of geometrical
patterns in the body shapes of animals [30, 45], and explains the symmetry and periodicity seen
in those structures. Reaction diffusion has also been shown to be
responsible for the pattern of markings on animal skins [ 42], which explains a diversity of stripes and
spots with a single unified theory. Studies of visual hallucination
patterns [ 10, 60], which
seem to afford a direct view of such harmonic resonances in the visual
system, also reveal characteristic symmetry and periodicity as seen in
harmonic oscillations.
Chapter 4:
Higher Level Representation of Visual Information
Introduction
Visual Abstraction of Image Vertices
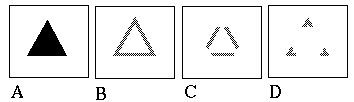
Figure 58
Temporal Frequency Encoding of Orientational Harmonics
Figure 59
Figure 60
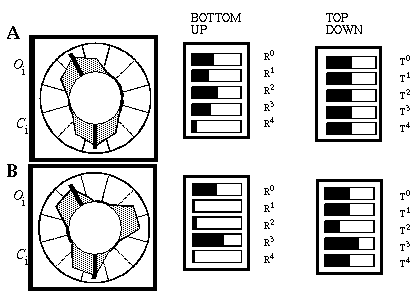
Figure 61
Figure 62
Rotation and Reflection Symmetry
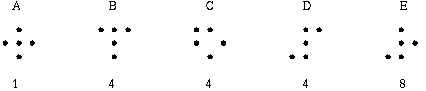
Figure 63
Conclusion
Figure 64
[6] Chladni, Ernst F. E. (1809) Traite d'Acoustique.
[8] Dennet, Daniel C. (1991). Consciousness Explained. Little Brown & Co., Boston.
[11] Farah, Martha J. (1990) Visual Agnosia. MIT Press, Cambridge MA.
[14] Garner, W. R. (1974). The Processing of Information and Structure. Erlbaum, Potomac MD.
[25] Hubel, D. H. (1988). Eye, Brain, and Vision, Scientific Americal Library, 79-80.
[27] Kanizsa, Gaetano (1976). Subjective Contours. The Mind's Eye, W. H. Freeman & Co., 82-86.
[35] Koffka, K. (1935) Principles of Gestalt Psychology. New York: Harcourt, Brace & World.
[37] Land E. H. (1977) The Retinex Theory of Color Vision. Scientific American, 237, 108-128.
[40] Metzger, W. (1975) Die Gesetze des Sehens. Frankfurt/M: W. Kramer.
[41] Miller, G. A. (1953) What Is Information Measurement? American Psychologist, 8, 3-11.
[47] Palmer,Stephen E. (1990) Modern Theories of Gestalt Perception. Mind & Language, 5, (4) 289-323
[55] Ramachandran, Vilayanur S. (May 1992). Blind Spots. Scientific American, 86-91.
[56] Ramachandran, V. S., & Gregory, R. L. (1991). Nature, 350, 699-702.
[64] Wait, R. & Mitchell, A. R. (1985) Finite element analysis and applications. J. Wiley, New York.