The Constructive Aspect of Visual Perception:
A Gestalt Field Theory Principle of Visual Reification Suggests a Phase Conjugate Mirror Principle of Perceptual Computation
Steven Lehar
Peli Lab
Schepens Eye Research Institute
20 Staniford St.
Boston, MA 02114
slehar@gmail.com
this paper also available at
.//ConstructiveAspect/ConstructiveAspect.html
.//ConstructiveAspect/ConstructiveAspect.pdf
Word Counts
Abstract: 224
Main text: 16,183
References: 879
Entire text: 19,852
Keywords
field theory
Gestalt
grassfire
inverse optics
phase conjugate
reification
spatial perception
Short Abstract
Many Gestalt illusions reveal a constructive aspect of perceptual processing where the experience contains more explicit spatial information than the visual stimulus on which it is based. The experience of Gestalt illusions often appears as volumetric spatial structures bounded by continuous colored surfaces embedded in a volumetric space. This suggests a field theory principle of visual representation and computation in the brain. A two-dimensional reverse grassfire algorithm, and a three-dimensional reverse shock scaffold algorithm are presented as examples of parallel spatial algorithms that address the inverse optics problem The phenomenon of phase conjugate mirrors is invoked as a possible mechanism.
Long Abstract
Many Gestalt illusions reveal a constructive, or generative aspect of perceptual processing where the experience contains more explicit spatial information than the visual stimulus on which it is based. The experience of Gestalt illusions often appears as volumetric spatial structures bounded by continuous colored surfaces embedded in a volumetric space. These, and many other phenomena, suggest a field theory principle of visual representation and computation in the brain. That is, an essential aspect of neurocomputation involves extended spatial fields of energy interacting in lawful ways across the tissue of the brain, as a spatial computation taking place in a spatial medium. The explicitly spatial parallel nature of field theory computation offers a solution to the otherwise intractable inverse optics problem; that is, to reverse the optical projection to the retina, and reconstruct the three-dimensional configuration of objects and surfaces in the world that is most likely to have been the cause of the two-dimensional stimulus. A two-dimensional reverse grassfire algorithm, and a three-dimensional reverse shock scaffold algorithm are presented as examples of parallel spatial algorithms that address the inverse optics problem by essentially constructing every possible spatial interpretation simultaneously in parallel, and then selecting from that infinite set, the subset of patterns that embody the greatest intrinsic symmetry. The principle of nonlinear wave phenomena and phase conjugate mirrors is invoked as a possible mechanism.
Keywords
diffusion
field theory
Gestalt
inverse optics
grassfire
illusion
phase conjugate
reification
shock scaffold
1. Introduction
There are many aspects of sensory and perceptual experience that exhibit a continuous spatial nature suggestive of a field theory principle of computation and/or representation in the brain. Visual experience appears in the form of a continuous space containing perceived objects that occupy discrete volumes of that space, with spatially extended colored surfaces observed on the exposed faces of perceived objects. It is a picture-like experience whose information content is equal to the information content of a three-dimensional painted model, like a museum diorama, or a theater set. A number of Gestalt illusions suggest a field-like computational principle in perception. For example the Kanizsa figure in Figure 1A appears as an illusory foreground figure that appears a brighter white than the white background against which it is seen. Even more compelling examples are seen in Peter Tse’s volumetric illusions shown in Figure 1 B and D. (Tse 1998, 1999), and Idesawa’s (1991) spiky sphere in Figure 1 C. It is clear that the visual system is adding information to the two-dimensional sensory input to create a three-dimensional perceptual experience that contains more explicit spatial information than the retinal stimulus on which it is based. However these spatial experiences might actually be expressed in the physical mechanism of the brain, the experience itself, as an experience, clearly appears in the form of a spatial structure.

Figure 1. A: Kanizsa figure. B: Tse’s volumetric worm. C: Idesawa’s spiky sphere. D: Tse’s sea monster.
1.1 Field Theory
A field theory computation is a computational mechanism that exploits a spatial field-like physical phenomenon as an essential component of the computation. Wolfgang Köhler (1924) cited a number of physical systems that exhibit field-like behavior, such as the way that electrical charge distributes itself across the surface of a conductor, or water seeks its own level in a vessel. Perhaps the most familiar Gestalt example of a field-like computational principle is the soap bubble (Koffka 1935). The spherical shape of a soap bubble is not encoded in the form of a spherical template, or abstract mathematical code, but rather that form emerges by the parallel action of innumerable local forces of surface tension acting in unison across the bubble surface.
1.2 Grassfire Metaphor
Soap bubbles, and water seeking its level, are spatial field-like processes, but they are not computational algorithms as such, until or unless they are deployed in some kind of computational mechanism. The grassfire metaphor (Blum 1973) on the other hand is a computational algorithm used in image processing that uses a field theory principle of computation to compute the medial axis skeleton of plane geometrical shapes, such as squares or circles or triangles. The idea is to ignite the perimeter of the geometrical pattern in question, and allow the flame front to propagate inward to the center of the figure like a grass fire. The medial axis skeleton is found at points and along lines where flame fronts from different directions meet. For example if a rectangular perimeter is ignited in this manner, the flame front will propagate inward from each of the four perimeter lines, with wave fronts parallel to the lines, as shown in Figure 2 A. The propagating flame fronts from orthogonal lines collide along diagonal fronts oriented 45 degrees to both original lines, tracing out the bisector to the angle between the two sides, as shown in gray lines in Figure 2 A. The medial axis skeletons for various geometrical forms are shown in Figure 2 B.

Figure 2. A: The grassfire algorithm for a rectangle, with the flame front propagating inward from the perimeter, marking the medial axis skeleton wherever flame fronts meet. B: The medial axis skeletons for various geometrical forms.
The grassfire algorithm is a mathematical abstraction rather than a field-like physical phenomenon. It exploits the regular propagation or diffusion of some idealized signal through a uniform medium, as the mechanism that performs the actual computation. The algorithm can be implemented in a variety of different physical ways, from actual lines of fire burning across a field of dry grass, to chemical reactions like the Belousov-Zhabotinsky reaction (Dupuis & Berland, 2004) involving reaction fronts that propagate uniformly through a chemical volume, to computer simulations of an idealized spatial signal propagating in an idealized medium. The grassfire algorithm is defined independent of any particular physical implementation of it, and when performed in computer simulation, it need not even use an explicit spatial matrix to compute its result. The algorithm does however require at least a virtual spatial matrix, a kind of computational blackboard across which to plot the advancing flame fronts, even if that matrix is actually stored in computer memory in a non-spatial configuration. In any case, the computational algorithm of that flame front must propagate the flame front correctly as if the propagation were taking place across a uniform spatial medium, if it is to compute the correct result. In other words, the computer simulation must be computationally equivalent to the explicit spatial propagation that it models.
1.3 Explicit versus Implicit Representation
The evidently spatial nature of the Gestalt aspects of experience raises a question about the neurophysiological implementation of those phenomena in the brain. If a field-like experience can be accurately modeled by a field-like computational algorithm propagating through a spatial medium, does the computational mechanism behind that algorithm in the brain necessarily have to be spatially extended, or can a volumetric spatial experience be represented in some kind of non-spatial or symbolic form in the brain? Non-spatial representations are commonly used in computer image representation, where the spatial grid of image pixels is either stored as long strings of values in sequential memory cells, or reduced to a symbolic code by image compression algorithms like those used in .gif and .jpg images, in which the raw pixel values are no longer readily available but require some kind of image decompression operation to retrieve. So the spatial information content of an image can be completely encoded in a non-spatial symbolic code that represents spatial structure, an implicit, rather than explicit spatial representation.
There are two issues regarding the necessity of an explicit representation in the brain. In an explicit spatial representation, spatial information is available immediately, without need for any kind of computation, whereas in an implicit representation the information must be unpacked, decoded, or decompressed, before explicit spatial information can be retrieved from it. For example the color of a point in an image can be read directly from that point in an explicit spatial image, from whence the neighboring points in the image are also immediately accessible by simple adjacency, whereas an implicit or compressed representation must be decompressed to retrieve a pixel value at some location, and its immediate neighbors. The fact that the spatial information of our immediate experience appears simultaneously and in parallel in the form of complete spatial wholes, suggests a representation in which that spatial information is already unpacked into the explicit spatial form in which it is experienced.
Secondly, it is not only the structure of visual experience that appears spatially structured, but the computational algorithm of perception also appears to exhibit dynamic spatial properties. For example the Kanizsa illusion in Figure 1A clearly involves spatial interactions between remote contours to form new illusory contours, and this interaction can be modeled as a spatial diffusion of the activation representing visual edges out into empty space, like a linear extrapolation of edges beyond their endpoints. (Lehar 1999) This kind of diffusion process requires immediate access to a specific geometrical region of spatially adjacent locations in the representation, and a means to propagate activation lawfully in specific directions through those adjacent locations, not unlike the grassfire concept. Of course a diffusion process of this sort can be simulated on a digital computer in which the image data is not stored in two-dimensional spatial grids, and in fact the computer simulations of the Kanizsa figure cited above were performed on digital computers that do not employ explicit spatially extended image representations. Nevertheless, a spatial field-like algorithm would be most efficiently implemented in a spatial field-like mechanism where the propagation proceeds in parallel, so if the algorithm of spatial perception were indeed shown to be a spatial field-like algorithm, that would strongly implicate, although not strictly require, a spatial field-like computational mechanism behind that algorithm in the brain.
In any case, if a computer algorithm correctly simulates an analog field-like computational process, which in turn correctly models some spatial phenomenon in experience, then the computer algorithm, the field-like neurophysiological process that it models, and the field-like experience or phenomenon that that model emulates, are effectively computationally equivalent, because they produce the same output for any given input. And if they are computationally equivalent, then it is equally valid to study the algorithm in either its implicit or explicit form, either as a computer algorithm processing digital data, or as waves of electrical energy propagating through neural tissue, or as fields of experienced contour, color, or motion interacting lawfully across phenomenal space. In fact, a spatial algorithm like a spatial diffusion process, is most simply described in its explicit spatial form as a straight diffusion of regions of activation into spatially adjacent regions, even if that algorithm is actually implemented in a computer simulation in non-pictorial memory, or in some non-spatial, or semi-spatial neurophysiological mechanism in the brain. I propose therefore to examine the functional algorithm of the brain as it manifests itself in experience, irrespective of whether that algorithm is implemented in explicit or implicit form in the brain. And the evidence presented below clearly indicates that the functional algorithm of the brain has explicit spatial aspects.
2 Evidence for an Explicit Spatial Representation
The evidence for an explicit spatial representation in the brain comes from a wide variety of diverse sources, from the structure of visual experience, to the nature of visual illusions. This evidence does not prove that the brain necessarily contains topographically explicit spatial images, because it is always possible to perform spatial computations in a computationally equivalent non-spatial form. However whether the brain encodes spatial information in explicit spatial form as actual “pictures in the head”, or whether it uses some more abstracted representation, one thing that the evidence does suggest is that the computational algorithm employed by the brain is an explicitly spatial one, and that in turn implicates a spatial computational mechanism in the brain.
2.1 Evidence from Visual Experience
Perhaps the most prominent evidence for a spatially reified explicit representation in the brain can be seen in the observed properties of visual experience. (Lehar 2003a, 2003b) For example the experience of a patch of blue sky is an experience of an extended spatial structure, every point of which is experienced simultaneously and in parallel to a certain resolution. In other words, visual experience is spatially extended, and that in turn suggests an explicit spatially extended representation in the visual brain in which each distinct point of experience is explicitly represented by distinct values. This representationalist notion of perception is passionately contested by proponents of the theory of direct perception (Gibson 1972, 1979, McLoughlin 2003, O’Regan 1992, Pessoa et al. 1998, Velmans 2000) who claim that our experience is not (or not necessarily) mediated by any kind of representational entity in our brain, but rather the world is experienced directly, out where it lies, beyond the sensory surface. We somehow become aware of the world beyond ourselves without the mediation of any kind of representation in our brain. But experience has an information content, and information cannot exist without some kind of carrier or medium to register that information. The phenomena of dreams and hallucinations clearly demonstrate the capacity of the brain to generate volumetric moving images of experienced information. Given the fact that these images require for their existence a living functioning brain, surely the images themselves could not be located anywhere other than in the physical brain.
In fact, the theory of direct perception is nothing more than an elaborate rationalization for naïve realism, the persistent belief that we can see the world directly, as if bypassing the causal chain of vision through the retina and optic nerve to the brain. For some people, even vision scientists, the sense of viewing the world directly is so vivid that they cannot bring themselves to contemplate, even as a theoretical possibility, that experience may be indirect. It is a paradigmatic choice, in the sense that this is an initial assumption, rather than a conclusion drawn from the evidence, because all of the evidence can be seen as supporting either view, depending on one’s initial assumptions. This is why debates on paradigmatic questions tend to become circular, because the opposing sides operate from different initial assumptions, and thus they often reach polar opposite conclusions based on the self-same evidence. (Kuhn 1970) But naïve realism is profoundly at odds with the causal chain of vision, whereby our experience is necessarily limited to patterns within our physical brain. If perception were direct, how could that property be built into an artificial vision system, to make it experience the world directly, out beyond its sensory surface? Direct perception tells us nothing about how such a system would have to be built, or how it would operate, except for the negative fact that it would supposedly not need any kind of internal representations. But robots without internal models are blind, because like people, robots cannot see or respond to anything that is not explicitly present either on their sensor array, or in a representation within their computer brain based on that sensory input. A robot cannot somehow have direct access to spatial information out in the world without the mediation of some kind of representation, and neither can a human brain. And direct perception offers no satisfactory explanation for the experience of dreams and hallucinations, items that could not possibly be perceived “directly” since there is nothing objectively real to be directly perceived. Unlike direct perception, representationalism does in fact make a very specific statement about the required architecture of a visual robot; that is, that a robot must have a full three-dimensional volumetric model of the world represented in its brain, if it is to behave as if it were seeing that world directly, out beyond the sensory surface. And representationalism offers the obvious explanation of dreams and hallucinations as images constructed by the brain.
The theory of direct perception is not a theory of how vision works, but merely a non-theory about how perception supposedly does not work. It offers no hint of how spatial information is represented in the brain, or how an artificial intelligence could possibly be built to exhibit this magical property of external perception. The time is long overdue to stop wasting our energies devising ever more clever and abstruse philosophical and theoretical rationalizations for how an explicit spatially reified volumetric experience could arise from a brain without explicit spatially reified volumetric representations, and focus instead on the more useful and concrete pursuit of working to identify the neurophysiological mechanism behind the volumetric moving colored imaging system in the brain that evidently underlies visual experience.
2.2 Evidence from Visual Illusions
Gestalt visual illusions provide direct evidence for an explicit spatial representation in vision. We have already discussed the Kaniza triangle shown in figure 1A, where an extended spatial structure is observed in the absence of any objective physical structure. Note how the illusory figures appears not only as a perceived contour, but as an explicit spatial surface, every point of which is experienced as a brighter white than the white background against which it is seen. Computer simulations of this illusory effect must involve not only the explicit tracing of the illusory contours between the stimulus edges in the figure, but also an explicit “filling-in” of a surface brightness percept at every point across the illusory figure (Grossberg & Todoroviçz 1988).
The computational process behind the formation of the Kanizsa illusion can be described as follows. The straight edges of the pac-man features appear to extend out beyond their endpoints by extrapolation, as indicated by the arrows in Figure 3A, where they meet with other extended edges coming from the opposite direction to form the illusory contour. This perceptual extrapolation can be modeled as a spatial diffusion of edges out beyond their endpoints in a collinear direction (Lehar 1999). The three contours in turn suggest the whole triangle as an enclosed figure. The percept of a triangle partially occluding three complete circles is geometrically simpler, or more statistically likely, than the chance alignment of three unrelated pac-man features, and thus this is the interpretation evidently preferred by the visual system. The contrast of this white illusory triangle against the black circles it appears to occlude imbues it with a white color that is perceived to be brighter than the white background against which it is seen, and this perceived brightness is observed to pervade every point across the whole illusory surface uniformly. Grossberg & Mingolla (1985) have modeled this perceptual computation as a spatial diffusion of color experience from the edges across which the dark/light contrast signal originates, filling in the entire illusory surface like water seeking its own level in a vessel, as suggested schematically in Figure 3B.

Figure 3. Illusory contour formation by A: diffusion of contour signal outward beyond contour endpoints, and B: diffusion of brightness signal inward to fill the bounding contour of the triangle with an experience of uniform brightness.
Even more compelling illusions in Figure 1 B through D (Tse 1998, 1999, Idesawa 1991) demonstrate the capacity of perception to generate full volumetric spatial experiences in which every point on every perceived surface has a separate and distinct perceived depth and surface orientation. Although the precise algorithm behind this perceptual computation remains obscure, it seems clear that some kind of spatial interpolation is occurring in three dimensions, where the two-dimensional information from stimulus edges is interpolated and/or extrapolated as actual colored surfaces extending into specific configurations in three dimensions (Lehar 2003a, 2003b). Again, a simplicity principle, or Gestalt tendency toward prägnanz, is in evidence here, whereby the final percept is the one that exhibits the simplest interpretation in a full three-dimensional context.
Consider the perceptual experience of the volumetric worm of Figure 1B, replicated below in Figure 4A. Clearly what is happening here computationally is an expansion of a two-dimensional stimulus into a full volumetric experience, as suggested in Figure 4 B, an inverse projection that seeks to reverse the optical projection of the eye, in which the light from a three-dimensional world is projected onto the flat surface of the retina. This is known as the inverse optics problem, a problem that is mathematically underconstrained, because there is an infinite range of different configurations of objects and surfaces in three dimensions that all project to the same two-dimensional stimulus. Although the computational algorithm behind this process remains obscure, it is an observational fact that among all possible interpretations of this stimulus, the final percept clearly favors the geometrical regularity of a cylindrical worm curved in a regular spiral around a cylindrical pillar.
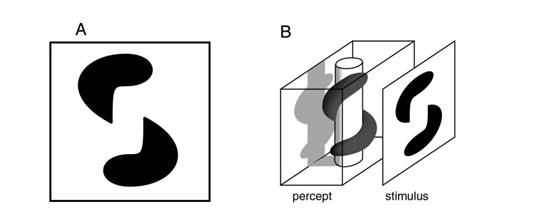
Figure 4. A: Tse’s volumetric worm produces an experience of B: a cylindrical worm wrapped in a regular spiral around a cylindrical pillar.
If it is an emergent spatial algorithm that is at work in these illusions, like a soap bubble surface, it is one that would have to operate in a fully volumetric spatial context, because the geometrical simplicity of the cylindrical shape of the perceived worm, and the regular spiral it forms in three dimensions around the cylindrical pillar, are not at all regular or simple in two-dimensional projection, and geometrical regularity, or simplicity, is the attractor that drives the dynamic system towards its stable state. By analogy, you could hardly expect a soap film to form a perfect spherical bubble if its emergent field-like computation actually took place in a two-dimensional projection, because in projection it is the flat circle, not the spherical surface, that is the simplest form. Likewise, you could not expect water to correctly seek its own level in a vessel if the emergent computation of that level were to take place in a two-dimensional projection of the vessel, because the two-dimensional projection of the water surface at equilibrium is not at all the simplest configuration in two dimensions, it is only in full three dimensions where that configuration is geometrically the simplest.
2.3 Neon Color Spreading, Brightness Assimilation, and Watercolor Illusion
Another perceptual diffusion of color experience is seen in the phenomenon of neon color spreading, one form of which is illustrated in Figure 5 A. Here the color from colored patches in the stimulus is perceived to diffuse outward to fill in a large region with a faint experience of color throughout that region, where it is observed to diffuse uniformly across the entire surface of the transparent percept, filling it with a uniform glow. The phenomenon of brightness assimilation (Musatti 1953, Helson 1963) shown in Figure 5 B exhibits a similar diffusion of perceived color or brightness. The background gray stripes in Figure 5 B are actually the same shade of gray inside as outside the figure, and yet the lighter color of the horizontal bars within the figure make that gray appear a lighter, or brighter gray, as if the brightness of the colored bars was leaking out of the bars themselves, and diffusing uniformly throughout the perceived figure, creating an impression of transparency, as if the gray tone were being viewed through a semi-transparent or milky film.

Figure 5. A and B: Neon color spreading, and brightness assimilation. C and D: The watercolor illusion.
A related phenomenon is seen in the watercolor illusion shown in Figure 5 C and D. The effect hardly works at all in monochrome, but in full color figures the effect is very compelling. Here, the color contrast originating along visual edges is experienced to fill in the areas bounded by those color contours, creating the experience of faint color across those regions, not unlike the faint colors of the neon color spreading effect. Like other Gestalt illusions, these phenomena are difficult to explain as some kind of cognitive inference, because the phenomena are pre-attentive and automatic, beyond the reach of cognitive influence, they are seen universally by virtually all subjects, and the success of the illusion depends critically on specific spatial configural factors, which suggest a low-level perceptual phenomenon.
2.4 Craik-O’Brien-Cornsweet Illusion
The Craik-O’Brien-Cornsweet Illusion (Craik 1966, O’Brien 1959, Cornsweet 1970) shown in Figure 6, also suggests a spatial diffusion of perceived color or brightness. In this illusion, a brightness “cusp” at the center of the figure, that is, an abrupt contrast edge that then fades back to neutral gray either side of the edge, creates an illusion of an absolute brightness step across that edge, with the gray shade the right half being perceived uniformly brighter than the same gray on the left half of the figure. The illusion can be destroyed by covering the cusp with a pencil, which reveals the same shade of on either side of the cusp. Again, it appears that the darkness from the dark side of the cusp diffuses outward from the edge to fill the whole rectangle of the left side with experienced darkness, as does the brightness from the bright side of the cusp to the right, resulting in an experience of an abrupt step in brightness between uniform gray regions either side of the cusp.

Figure 6. The Craik-O’Brien-Cornsweet illusion appears uniformly darker on the left half than on the right, due to a brightness “cusp”, or sharp step in brightness along the center, fading to uniform gray on either side. The illusion is revealed by hiding the vertical cusp with a pencil.
2.5 Evidence from Simultaneous Contrast
The simultaneous contrast illusion shown in Figure 7 provides further evidence for a spatial process in the construction of experience. The color of the central gray square appears brighter against a dark surround in Figure 7 A, and darker against a bright surround in Figure 7 B. This difference in perceived brightness is experienced uniformly throughout each gray square. Simultaneous contrast and brightness assimilation are related quasi-complementary processes, the contrast effect deriving from the contrast across the perimeter of the gray square, while its uniform illusory brightness is a manifestation of the assimilation effect, filling-in the region within a contour with a uniform color experience.

Figure 7. Simultaneous Contrast Effect. The color of the central gray square appears brighter against a dark surround in A, and darker with a bright surround in B. This difference in perceived brightness is experienced as a uniform expanse of color with the anomalous brightness expressed throughout.
2.6 Evidence from Apparent Motion
Further evidence for visual reification is seen in the phenomenon of apparent motion. (Wertheimer 1912) For example a pair of adjacent lights that blink on and off alternately create the illusion of a single light jumping back and forth between the two lights. The fact that this is a low level perceptual phenomenon is demonstrated by the fact that the illusion depends critically on the exact timing of the stimulus. When the inter-stimulus interval between the two lights is very brief, observers see two lights that appear and disappear simultaneously. When the interval is too long, observers see a light, followed by a second light, without any apparent motion between them. The full illusory motion is achieved only when the spatial and temporal parameters fall within strict limits, and those limits are not influenced by cognitive considerations. The spatial and temporal parameters are interdependent; when the stimuli are separated by a larger distances, longer time intervals are required between the stimuli for the illusory motion to be perceived. And when the illusion succeeds, it does not appear in the form of a cognitive inference, an abstract knowledge or supposition of a motion, but rather there is an actual spatial experience that takes the form of a colored light moving through space and time that is virtually indistinguishable from an actual moving stimulus. If the stimulus lights are colored, the moving percept is also colored. And if the two lights are of different color, for example one red and the other green, then the illusory percept is not experienced as of ambiguous or undefined color, nor an intermediate brownish hue, but rather the color is observed to switch abruptly half way along its illusory path, as if viewing a moving white light through transparent red and green panes of glass. When the alternating stimuli are of different shapes, for example a square on the left and a circle on the right, then the illusory object is perceived to morph continuously as it jumps back and forth between the two stimulus lights. When the path of the illusory motion is blocked by a visible obstacle along the path, the illusory object is experienced to make excursions into the third dimension so as to appear to pass either in front of, or behind the obstacle. (Coren et al. 1994)
It is clear that the visual system is making use of a constructive, or generative algorithm in apparent motion, one that constructs a specific, reified, spatially extended visual experience of an object moving through space, and therefore there must be some kind of physical substrate or “screen” on which that constructed image is maintained or registered in the brain while we are having that spatial experience.
2.7 Evidence from Blind Spot Experience
Another example of visual reification is seen in the experience of the retinal blind spot, due to the absence of sensory rods and cones where the optic nerve penetrates the retina at the back of the eyeball. Naive subjects are totally unaware of this gaping hole in their visual field, because the visual field at the location of the blind spot is experienced to have the color of whatever surrounds it. When viewing the blind spot against a white background, it appears as a continuous white surface, whereas when viewing against a pink surface it takes on a pink color. This is further evidence for a kind of perceptual filling-in where the color of the background diffuses or bleeds into the blind spot region creating a continuous field of experienced color, every point of which is experienced as a separate parallel color experience, and all of those points are experienced simultaneously as a spatial continuum of color to some resolution.
Dennett (1992) argues that the neural representation of a filled-in percept need not involve an explicit filled-in representation, but can entail only an implicit encoding based on a more scanty representation. This idea is supported by the fact that retinal ganglion cells appear to respond to spatial discontinuities of the retinal image, that is, visual edges, which suggests that the retinal image is some kind of edge representation, encoding an image much like the stimulus of the watercolor illusion. Rather than an explicit filling-in computation, Dennett argues that the visual system simply “ignores the absence” of data across the retinal blind spot, (Dennett 1992, p. 48) and that ignorance of the absence of stimulation is experienced as a continuous colored surface. But the notion of perception by "ignoring an absence" is meaningful only in a system that has already encoded the scene in which the absent feature can be ignored. In the case of the blind spot, that scene is a two-dimensional surface percept, every point of which is experienced individually and simultaneously at distinct locations as a continuous colored experience. In other words, the experience has a specific information content that is simultaneously present in the experience as a spatial structure, and information cannot exist without being explicitly stored or registered in some physical medium.
But even if Dennett were right, that the brain does not need to construct the spatial structures of our experience, but can encode them exclusively in some abstract, compressed, non-spatial representation, our experience of that representation is nevertheless an experience of an explicit spatially structured world. So something in our mind or brain would have to be constantly reading that non-spatial brain state and reifying its abstract code to create the structured world of our experience. So the reification must be computed somewhere in the brain or mind for us to experience it as reified. Even if spatial experience had no presence in the physical world, and existed only in some orthogonal subjective plane of existence, as some theorists have proposed, experience, as an experience, is nevertheless spatially structured in a pictorial, analogical form. And the analogical form of that experience is neither coincidental nor inconsequential, it is an essential aspect of the world of our experience without which our visual experience would be truly blind.
2.8 Retinal Stabilization Evidence
The diffusive filling-in of the retinal image has been tracked in retinal stabilization experiments in which portions of a stimulus are stabilized on the retina so as to eliminate the constant jittering of the image due to ocular micro-saccades. When a retinal image is stabilized in this manner, the stimulus disappears to the subject entirely, demonstrating that the constant jitter is required for the retina to detect even static features. This phenomenon has been used to examine retinal filling-in by devising stimuli in which some edges are stabilized, to disappear to the subject, while others remain un-stabilized, and thus they remain visible. For example Yarbus (1967) devised a stimulus in the form of two concentric disks of different colors, for example a small red disk at the center of a larger green disk, viewed against a gray background. When the perimeter of the smaller red disk is selectively stabilized against the retina, then not only does that contour disappear to the subject, but the color of the central disk also disappears as it is swamped by the color of the surrounding green disk that is observed to diffuse its green color over the area of the invisible red disk, even at locations where the stimulus is actually red. The fact that the red color disappears even though only the outer contour of the red circle is stabilized, clearly indicates that the experience of surface color within enclosed contours is reconstructed or filled-in by diffusion from the color contrast at the stimulus contours, in this case from the green/gray contrast at the perimeter of the larger green disk. This is consistent with the findings of Land & McCann (1971) for the perception of colored patches, in which the perceived color of a patch is determined by its color contrast with neighboring patches, rather than by its intrinsic color.
2.9 Delayed Masking Evidence
The speed of the diffusion of perceived color has been measured psychophysically in delayed masking experiments (Paradiso & Nakayama 1991). A colored disk is presented very briefly to the subject, followed immediately by another brief stimulus of an outline circle at the same location. If the inter-stimulus interval (ISI) between the disk and the circle stimulus is sufficiently brief, the experience of the colored disk is swamped, or overwritten by the subsequent circle percept by backward masking, and the subject reports seeing only the outline circle. If the outline circle is smaller in radius than the colored disk, then it masks only the central portion of the stimulus, and subjects report the experience of a colored annulus with outer radius equal to that of the larger colored disk, and inner radius equal to that of the outline circle, with no color experience within the outline circle. This suggests that the color contrast at the outer perimeter of the colored disk triggers a color signal that diffuses inward toward the center of the disk filling the disk with experienced color, but the diffusion is abruptly blocked at the radius of the outline circle when it suddenly appears, creating the experience of a colored annulus up to that point. If however the inter-stimulus interval (ISI) between the colored disk and the outline circle is too great, then the backward masking fails, the color is observed to fill in the larger disk completely, and subjects report seeing a uniform colored disk followed by an outline circle. Significantly, the threshold ISI value required to produce the annular percept is observed to vary as a function of the difference in radius between the outer color disk and inner masking circle, with larger ISI required when the masking circle is smaller, presumably because it takes longer for the color signal to diffuse across the greater distance. This experiment clearly demonstrates that the diffusion of color experience is not an abstract cognitive inference, or some kind of vague, non-spatial knowledge, but is an actual spatial diffusion of a spatial color signal at a specific rate across perceived space, as a spatial computation taking place across a spatial medium.
3 Computational Function Served by Field Theory Algorithm
The most interesting thing about the field-like processes apparently active in perception is the computational function that is apparently served by those processes. Gestalt phenomena reveal a unique principle of perceptual computation that is quite unlike anything devised by man, and very different from the principle of operation of the digital computer. It is an emergent computational strategy that searches a practically infinite solution space in a finite, almost instantaneous time. And the end result of this processing is not just an abstract recognition of features detected in the visual field, but an explicit structural reconstruction of the scene considered most likely to have been the cause of the stimulus.
3.1 Retinal Filling-In
The computational purpose behind the field-like computational processes of perception can be seen most clearly in the various retinal filling-in phenomena. The blind spot filling-in phenomenon demonstrates how experienced color flows or diffuses almost instantaneously across regions of missing data, and the delayed-masking experiments measure the rate of flow of this diffusion of experienced color. The retinal stabilization experiments demonstrate how the diffusion is blocked or channeled by the presence of contrast edges, which also provide the color signal to diffuse.
Retinal ganglion cells have been shown to respond only along visual edges, not in regions of uniform brightness or darkness. So the ganglion cell response to a Kanizsa figure stimulus in Figure 8 A would be something like an edge image that records the direction of contrast across image edges, as suggested in Figure 8 B, where the white lines show the response of on-center off-surround ganglion cells on the bright side of contours, while the dark lines show the response of off-center on-surround cells on the dark sides of contours, and the neutral gray tone indicates zero response from either cell type. This image serves as the source for the spatial diffusion of brightness outward from the pac-man figures, and darkness inward within each pac-man figure, (Grossberg & Todorovic 1988, Lehar 1999a) as suggested progressively from Figure 8 B through E. It is as if the visual system were computing a spatial derivative, the edge image, preserving only brightness changes across space, followed by a spatial integral, in which the surface brightness information that was lost in the edge detection is recovered again by diffusion.
Why would the visual system perform what is essentially a forward transform followed immediately by its inverse? Grossberg (Grossberg & Mingolla 1985, Grossberg & Todorivic 1988) suggests that the reason for this processing is to discount the illuminant; that is, to record the pattern of the stimulus independent of the strength of the illumination. The edge image of Figure 8 B records the local ratio of brightness across visual edges, and thus this image is largely invariant to changes in the overall brightness or illumination of the stimulus image, and thus the surface-brightness image reconstructed from that edge image would also remain largely invariant to illumination. (For a simulation of this effect, see figure 12 in Lehar 1999a available on-line) This process also serves to fill in any missing data, as in the retinal blind spot.

Figure 8. Retinal filling-in. A: The Kanizsa stimulus promotes B: a retinal edge image that serves as the source of darkness and brightness signals for (C though E) a spatial diffusion of color or brightness except where bounded by stimulus edges.
The spatial diffusion of experienced color in the filling-in phenomena can be seen as an expression of the Gestalt law of similarity, in this case enforcing the law that in the absence of contradictory evidence (in the form of visual edges) the visual system assumes that the color throughout a featureless region will be the same as the color contrast averaged around the boundary of that region. And the implications of that assumption are computed as in the grassfire algorithm, by a uniform isotropic propagation of a spatial color signal through a spatial medium, filling-in all perceived surfaces with the colors they are assumed to have. Whatever the purpose of this peculiar forward-and-inverse processing in perception, this concept at least explains a great variety of visual illusory effects, such as the watercolor illusion, the Craik-O’Brien-Cornsweet illusion, the brightness contrast illusion, (for computer simulations see figures 12 – 14 in Lehar 1999a) certain aspects of brightness assimilation, blind spot filling-in, the retinal stabilization experiments, and delayed-masking experimental results.
3.2 Illusory Boundary Completion
The illusory boundary completion observed in the Kanizsa illusion can be modeled by a directed diffusion of contour information across the gap. (Lehar 1999b) Figure 9 A shows a retinal edge image of the Kanizsa stimulus. Figure 9 B and C show the straight edge segments diffusing across the gap by linear extrapolation/interpolation to create the illusory contours. Surface brightness filling-in on this completed boundary creates the full illusory figure, as suggested in Figure 9 D and E. As in the case of brightness filling-in, one function served by this forward and inverse process is to reconstruct visual edges across gaps and occlusions, like the gaps of missing data caused by retinal veins and the blind spot. (Grossberg & Mingolla 1985) This process can be seen as an expression of the Gestalt law of good continuation: That in the absence of contradictory evidence, a visual edge will be assumed to extend out beyond its endpoint when it can link up with other edges that are in a configuration of good continuation. The general computation principle appears to be to extract the invariants from the image, in this case contrast edges at particular orientations, and to use those detected features to fill-in the rest of the scene, in this case by extrapolation of linear contours beyond their endpoints, and interpolation of those extrapolated edges across the gaps between collinear stimuli, followed by a filling-in of color experience throughout regions enclosed by a contour.

Figure 9. Illusory contour completion. A: the retinal image records the brightness transitions in an edge image. B and C: A directed diffusion of edge information fills in the illusory contour. D and E: Surface brightness filling-in creates the percept of a filled-in illusory figure that is brighter than its background.
3.3 Volumetric Perception
The Kanizsa illusion is not confined to two dimensions, it includes a vivid sense of depth, as a foreground surface occluding background circles, as suggested in Figure 10 A. This permits boundary completion to occur not only on the illusory foreground figure, but also on the three pac-man features that are occluded by it, which are now perceived as full circles, completing amodally behind the illusory surface, as suggested in Figure 10 B. This kind of contour is called amodal (Michotte 1991, 1967) because it is not associated with any visual modality, such as a change in color, or texture, or motion, across the edge. However despite the fact that the amodal contour is “invisible” in any visual modality, it is nevertheless a spatial structure that is clearly experienced, and it is experienced at a precise location that can be easily traced with a pencil, making the pac-man features appear as full uninterrupted circles in perception, behind an occluding figure. Amodal perception is perception in the absence of direct sensation.
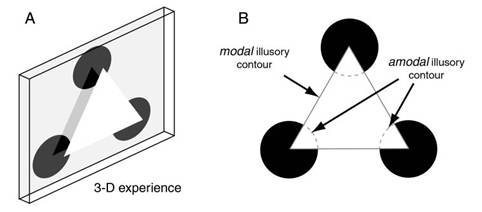
Figure 10. A: The three-dimensional perceptual experience due to the Kanizsa figure comprising B: modal and amodal illusory contours.
The full volumetric nature of illusory boundary completion and surface brightness filling-in, can be seen clearly in the subjective Necker cube illusion shown in Figure 11 A, that creates the illusion of a full volumetric spatial structure composed of illusory bars suspended in space, as suggested in Figure 11 B. Note how the intersection of the two illusory contours towards the lower right of Figure 11 A, reverses completely with the reversal of the subjective Necker cube, with the vertical and horizontal illusory bars taking turns occluding each other, as suggested for one of those states in Figure 11 B.
In fact, the volumetric nature of illusory contour and surface formation is already evident in the fact that viewing a Kanizsa stimulus, or any other illusion, obliquely, as suggested in Figure 14 C, creates an illusory figure within the plane of the stimulus. That is, the illusory figure does not remain in the frontoparallel plane, but illusory contour formation and surface brightness filling-in occur obliquely in depth within the stimulus surface to create an illusory surface sloping in depth.

Figure 11. A: The Subjective Necker Cube illusion promotes an experience of B: volumetric illusory structures in space, that reverse in synch with the reversal of the Necker cube illusion. C: Even a flat Kanizsa stimulus viewed in perspective promotes an illusory figure sloping in depth within the plane of the stimulus.
Volumetric three-dimensional versions of the Kanizsa figure can be constructed from cut-out sheets of acrylic attached to a circular frame, as shown in Figure 12 A. When viewed against a distant background, the illusory surface appears at the depth of the foreground stimulus, even when viewed obliquely in depth, as shown in the figure, where the illusory brightness appears as a volumetric illusory slab hanging in space, sloping in depth, glowing faintly like the neon color illusion, with a perceived thickness equal to the thickness of the acrylic stimuli. A similar effect can be achieved using a three-dimensional version of the Ehrenstein illusion, shown in Figure 12 B (Ware & Kennedy 1977). The illusion is hardly visible in the photographs of Figure 12, which are presented here merely to illustrate the configuration of the stimulus. In live viewing the illusory effect is accentuated by waving the stimulus gently back and forth against the background. The appearance of these volumetric illusory figures clearly demonstrates that boundary completion and surface brightness filling-in operate as three-dimensional volumetric processes.

Figure 12. Volumetric version of A: the Kanizsa figure, and B: the Ehrenstein illusion. When viewed against a distant background the illusory figure is observed to hang suspended in empty space at the depth of the stimulus, where it is seen to glow faintly like the neon color illusion. (The illusion is much less vivid in these photographs than it is in live viewing)
3.4 Inverse Optics Projection
The primary function of visual perception appears to be to solve the inverse optics problem, that is, to reverse the optical projection of the eye, in which information from a three-dimensional world is projected onto the two-dimensional retina. But the inverse optics problem is underconstrained, because there are an infinite number of three-dimensional configurations that can give rise to the same two-dimensional projection. How does the visual system select from this infinite range of possible percepts to produce the single perceptual interpretation observed phenomenally?
Hochberg & Brooks (1960) showed that the visual system tends to select the simplest possible interpretation of the stimulus, whether in two dimensions or three, as determined by the number of different sized angles in the interpretation, and the number of different lengths of the line segments. For example Figure 13 A tends to be perceived as a three-dimensional cube, with all equal length sides and all right angled corners, because that is a simpler interpretation than the two-dimensional projection of that stimulus containing different line lengths and odd angles. Figures 13 B through D exhibit progressively simpler, or more regular two-dimensional projections of that same three-dimensional cube viewed from different angles, and thus these stimuli are progressively less likely to be perceived as three-dimensional forms, and more likely to be interpreted as flat two-dimensional figures, although most of them can be seen either way, with greater or lesser effort. Hochberg & Brooks were the first to quantify the Gestalt principle of prägnanz, that is, the general tendency to perceive the simplest possible interpretation of the stimulus.

Figure 13. Hochberg & Brooks (1960) showed that the probability that a figure is perceived as a three-dimensional object varies as a function of the geometrical simplicity of its two-dimensional projection; the simpler the two-dimensional interpretation, seen here increasing progressively from A through D, the more likely that figure will be perceived as two-dimensional.
The mystery behind this, and other Gestalt perceptual phenomena, is the immediacy and vividness with which the visual mind arrives at an interpretation. It is an unconscious process, and usually instantaneous, except in ambiguous or bistable cases where the percept can alternate endlessly, and the experience of this visual computation is a volumetric spatial image that sometimes vacillates between alternate states. All of this suggests a parallel analog computational process, involving spatial interactions in a volumetric spatial medium, whose stable states represent the final percept. Indeed, a parallel algorithm is exactly what is required to search the infinite possibilities of the inverse optics problem and pick out the simplest interpretation or interpretations from that infinite set in a finite time. Because the regularity of the cubical interpretation is entirely absent from the stimulus, and must be reified into full three-dimensional depth where its regularity can be more easily detected by parallel analog field-like computational processes.
3.5 Shock Scaffolds
There is a three-dimensional extension to the grassfire algorithm, known as shock scaffolds, (Leymarie 2003) used to compute the three-dimensional medial axis skeletons of volumetric forms such as spheres and cubes, by the same principle that the grassfire metaphor uses in two dimensions. Instead of igniting the perimeter of a two-dimensional figure, the outer surface of a volumetric form is ignited, which creates a flame front parallel to each surface, and propagating outward normal to the surface. The locations where these propagating flame fronts meet, define the three-dimensional medial axis skeleton as three-dimensional surfaces in space. For example Figure 14 A shows the shock scaffold pattern due to a dihedral composed of two intersecting planes. A set of wave fronts is depicted, propagating outward from each plane surface in a direction normal to the surface. The shock scaffold, or medial axis, depicted in gray shading, defines a third plane that forms the angular bisector between the dihedral planes, as shown in Figure 14 A. Every point in the shock scaffold is equidistant from both planes of the dihedral. Figure 14 B shows the shock scaffold due to a trihedral corner. Each of the three dihedral pairs of the trihedral forms a shock scaffold at the angular bisector, and the three angular bisector planes intersect each other along a ray centered on the trihedral solid angle, shown as a dark gray ray in Figure 14 B. This ray is a higher order shock scaffold, a symmetry of symmetries. Every point along this ray is equidistant from all three planes. Figure 14 C shows the shock scaffold for a cylindrical shell. The propagating waves form concentric cylindrical shells that converge on a focal line along their common cylindrical axis. And Figure 14 D shows the shock scaffold for a spherical shell segment, that generates wave fronts that converge in spherical shells to a focal point, a punctuate shock scaffold. The energy of the wave becomes concentrated as a large wave converges to occupy a smaller area, and this concentration ratio increases progressively for the higher order symmetries in Figure 14 A through D, as suggested by the increasingly dark shading in the figure. The concentration ratio seems to correlate with the perceptual emphasis on these symmetries.

Figure 14. A: Shock scaffold (gray shading) for a dihedral forms where the propagating wave fronts from each plane surface meet. B: Shock scaffold for a trihedral forms along the intersection of the three shock scaffolds for each of the three pairs of planes. C: Shock scaffold for cylindrical surface forms a focal line. D: Shock scaffold for a spherical surface forms a focal point.
Figure 15 shows the shock scaffolds for a variety of volumetric forms. The gray shade indicates the approximate concentration ratio for each axis of symmetry. Whether the visual system uses a shock scaffold or grassfire propagation type of algorithm remains to be determined. But whatever the algorithm used in visual perception, it is one that appears to pick out the simplest volumetric interpretation in a volumetric spatial medium, from amongst an infinite range of possible interpretations, and it does so in a finite time. The shock scaffold algorithm offers one way that this kind of computation can be performed. The shock scaffold algorithm also explains why the brain would bother to do this computation in full volumetric 3-D, instead of in some abstracted or compressed or symbolic spatial code, as is usually assumed. Because it is easier to pick out the volumetric regularity of an interpretation from an infinite range of possible alternative interpretations, if searched simultaneously in parallel, than it is to find that regularity where it is not explicitly present in the two-dimensional projection or other abstracted representation.
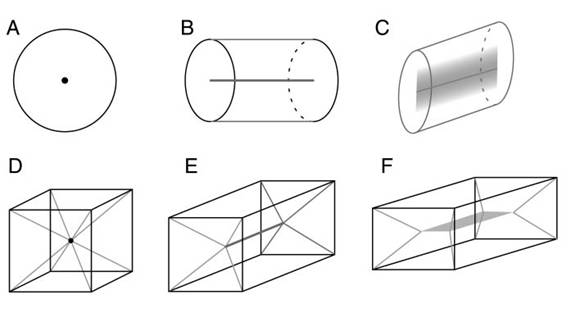
Figure 15. Shock scaffolds for various geometrical forms. A: Sphere. B: Cylinder. C: Elliptical cylinder. D: Cube. E: Square cross-section box. F: Rectangular cross-section box.
3.6 From Abstraction to Reification: A Reverse Grassfire Algorithm
The visual illusions shown in Figure 1 demonstrate that perception can be factored into two distinct types of computational operation, abstraction and reification. Abstraction is the extraction or recognition of particular patterns in the stimulus, for example a recognition of the circular forms of the three incomplete-circular pac-man features in Figure 1 A, and of the triangular symmetry of the illusory figure. Reification is the filling-in or perceptual completion of the missing portions of patterns that are detected. This is seen in the illusory boundary completion by extending the collinearity of stimulus edges out into empty space, if they can link up with other edges to form longer contours. The reification does not end with the construction of the illusory contours, but those contours are seen as parts of a larger triangular figure, and that triangle is “painted in” or reified, making explicit the triangular pattern detected implicitly in the stimulus. Another form of reification is seen in the amodal completion of the pac-man features into complete circles in perception. I propose that the reification of features observed in perception is computed as a kind of pseudo-inverse processing of the bottom-up feed-forward processes by which those features were detected in the first place. The grassfire algorithm can be used to clarify this concept by adding a second, reverse-grassfire processing stage to perform the reification.
Consider a grassfire algorithm applied to the stimulus of an incomplete three-quarter circular perimeter, as shown in Figure 16 A. The circular symmetry of this partial perimeter will propagate a wave front following concentric arcs towards a focal point at the circular center. The circular symmetry of the stimulus could thus be detected at that central point by an algorithm that accumulates a histogram of the time of arrival of flame fronts at that location, since the ignition of the flame propagation. In other words, the moment the flame front is ignited, every pixel in the image resets a clock, and records a time histogram of the arrivals of flame fronts from any direction at that pixel’s location, as shown for four pixel locations in a complete circle in Figure 16 B. The pixel located at the circular center will record a single large peak after a time interval proportional to the radius of the circular arc, due to the time taken for the flame to propagate across that radius. Pixels just off-center will record a broader and lower amplitude pulse, starting sooner and ending later, whereas pixels near the circumference will record one continuous wide but low amplitude pulse, starting with the arrival of the flame front from the nearest point of the circumference, and ending with the front from the farthest point, as suggested in Figure 16 B. A “circle detector” could be defined to detect the presence of the circular center of symmetry by detecting a large spike in the arrival-time histogram, where the flame fronts from the entire perimeter arrive at the same instant. The radius of the detected circle can be computed from the time delay of that spike since the start of flame propagation.
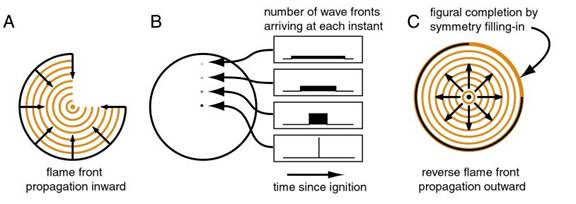
Figure 16. Figural completion by reverse grassfire algorithm. A: Grassfire algorithm for partial circular perimeter. B: The time trace histogram of the number of wave fronts arriving each instant at four sample points in the circle. C: The reverse grassfire algorithm propagates flame fronts back out again from the detected center, and prints the final shape after a time delay.
Once a circle is detected, the process is reversed by reflecting the converging wave back out again from the focal point, back in the direction from whence it came, as an expanding circular arc, as suggested in Figure 16 C. After a time interval equal to the original time delay for that wave, the expanding wave front is abruptly stopped and “printed” as an experience at its current location in the computational matrix, as suggested in Figure 16 D. This “printed” image is a “top-down” confirmation of the circle that would be expected, given the circular symmetry detected at the circular focus. If the top-down reflected wave were to reflect each ray individually, the reconstructed form would exhibit the same gap of missing data in the top right quadrant. But the top-down reflection can also be defined by reversing the average of all incoming waves, sending out a reflection of that average in all directions isotropically. This would serve to complete the circular symmetry across gaps or occlusions in the data, as shown in Figure 16 C. This process enforces the Gestalt law of “Symmetry”.
Detecting and completing the central symmetry of a square is only a little more complex. After igniting the perimeter of a square, the four points where orthogonal flame fronts intersect at the four corners of the shrinking rectangular flame front, form four vertices traveling rapidly along the diagonals, converging towards the center of the square, as suggested in Figure 17 A. When the flame fronts collide at the center of the square, the collision has a four-fold pattern of symmetry to it, with energy coming from the direction of the four diagonals, as suggested in Figure 17 B. What is required of a top-down mechanism is an exact reversal of this process, to paint out and complete the whole square based on its detected four-fold symmetry.
The central collision of vertices can be reflected back outward by projecting four vertices outward along the diagonals, in a mirror reversal of their pattern of inward collision, as suggested in Figure 17 C. These outward-propagating vertices must then be defined to reverse the inward pattern of waves that generated them, creating orthogonal pairs of propagating wave fronts traveling back outward towards the perimeter, as suggested in Figure 17 D, like bow waves from moving boats. These orthogonal outward-propagating fronts must be exact time-reversed replicas of the incoming wave fronts that triggered the corner symmetry detector bottom-up. And after a time interval proportional to the size of the square, the expanding square perimeter is abruptly stopped, and “printed” in the experiential matrix, as suggested in Figure 17 E. This sequence of bottom-up detection of a compound symmetry, followed by a top-down reification of that symmetry in a spatial medium, allows for perceptual completion of regular polygons by the same general principle as the linear completion of edges, and the diffusive filling-in of experienced color.
.
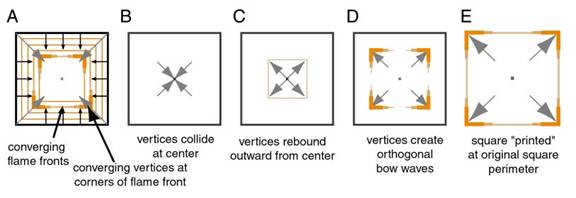
Figure 17. A: Inward propagating flame front with four vertices propagating towards the center. B: The vertices collide at the center in a diagonal symmetry. C: The flame front vertices reverse and propagate outward again. D: Each flame front vertex creates orthogonal “bow waves” for the edges of the square. E: When propagation is complete, the square is “printed” at that location as a reconstruction of the central symmetry detected in the square.
The description presented above is rather vague and not fully specified as either a perceptual model or a computational algorithm. It is more of a metaphor for a certain concept of reciprocal field-like computational processing, rather than a detailed model as such. Nevertheless, it is significant that light rays (and other wave phenomena) are reversible, so that any optical or wave type system that works in one direction, also works in the opposite direction, where it performs the exact inverse function, as you see when looking through a telescope from the wrong end. So it is not unreasonable to suppose that the inward converging wave fronts can also be reversed across the “focal point” of a center of symmetry by an amplified reflection of some sort across that point. In fact, the nonlinear wave phenomenon of phase conjugation performs exactly this kind of time-reverse outward reflection of an incoming wave front, as will be discussed below. In any case, whether perception employs anything like a reverse grassfire or shock scaffold or phase conjugate type algorithm, the effect of visual processing clearly exhibits properties as if perception were using some kind of reverse grassfire type principle in perceptual reification, in which central symmetries that are detected in the stimulus are interpolated and/or extrapolated back out again to produce an explicit volumetric structure in experience, as the simplest, most geometrical regular structural interpretation of stimulus.
The principle of visual abstraction is well known, and is embodied in a number of different models of perceptual processing. The complementary function of visual reification on the other hand is possibly the single most under-recognized and under-acknowledged aspect of perceptual processing.
3.7 Volumetric Spatial Reification
The idea of perception as a forward-and-inverse process of abstraction and reification, can explain the perception of a number of simple line drawing figures. Consider a visual stimulus of a simple ellipse, as shown in Figure 18 A. By itself this stimulus tends to be perceived as an ellipse, but given a little additional context, it can also be perceived as a circle viewed in perspective. But the symmetry of the circle is entirely absent from the stimulus, so the circular symmetry must be reconstructed by reification in a volumetric spatial medium before it can be detected. Figure 18 B shows an inverse-optics inverse-projection of the ellipse, that defines an elliptical cylinder in depth. The inverse projection distributes each stimulus line uniformly across the depth dimension. The surface of this cylinder defines the locus of all possible edges in the three-dimensional world that could have projected to the elliptical pattern of this two-dimensional stimulus. A volumetric spatial algorithm like the shock scaffold algorithm can then be used to seek out the most regular spatial interpretations of this inverse projection, as follows.

Figure 18. A: A two-dimensional stimulus of an ellipse, that can be perceived as a circle in projection. B: The inverse-optics inverse-projection of that ellipse defines an elliptical cylinder in depth, shown in light gray shade. The medial axis skeleton of the elliptical cylinder appears as a flat surface depicted at the center of the form. C: A perfect tilted circle embedded within the elliptical cylinder propagates concentric waves that converge to a focal point. D: Another tilted circle, tilted in the opposite direction, also embedded in the elliptical cylinder. E: A bi-stable percept that alternates between two sloping circular percepts in depth.
Every point in the surface of the elliptical cylinder in Figure 18 B becomes an ignition point for a volumetric shock -scaffold-type wave propagation creating a locally planar flame front propagating normal to the ignition surface. In this case, the flame front is shaped like an elliptical cylinder, shrinking to its medial axis, which forms a flat region across the axis of the ellipse, due to the elliptical asymmetry, as shown in darker gray shading in Figure 18 B.
The elliptical cylinder extruded from the stimulus ellipse contains perfect plane circles embedded within it obliquely, as shown in Figure 18 C and D, and these circles have a perfect circular symmetry that could be detected at their center, by the perfect convergence of propagating wave fronts at those circular centers. In other words, at that special point, the circular symmetry around that point is manifest by the abrupt synchronized arrival of propagating waves from all directions simultaneously, within a disc around a tilted central axis to a focal point, as suggested by the arrows in Figure 18 C and D. A detector located at this special point, tuned to respond to such coincidental arrivals, would serve as a “circle detector” that would respond to the presence, not of circles in the stimulus, but of circles embedded in the inverse-projection of the stimulus.
The top-down reification computation can also be performed in the volumetric shock scaffold representation to complete volumetric symmetries that are detected. Starting at the center of circular symmetry, a reflection of the incoming wave front pattern would project out in a tilted circle expanding outward, as suggested in Figure 19 A, in a time-reversed replica of the incoming waveform. After a time interval equal to the original time delay, that expanding circle is “printed” in experience as a volumetric spatial pattern, as suggested in Figure 19 B, or as the alternate interpretation in Figure 18 D. Since these two alternatives are mutually exclusive, the visual system becomes bistable between these two states, as suggested in Figure 18 E.

Figure 19. A: The reverse grassfire algorithm propagates outward from the detected center of circular symmetry in a time-reversed reflection of the incoming wave that triggered it. B: After a time interval equal to the original time delay of the circular symmetry detection, the outward propagating circle is “printed” at that radius, creating C: a perceptual interpretation of the elliptical stimulus as a perfect circle viewed in perspective.
The symmetry of the circular form is entirely absent from the elliptical stimulus, but it is recreated again, along with an infinite range of other possible forms, by the inverse projection, from whence a symmetry detector picks out and amplifies the pattern or patterns with the greatest volumetric symmetry.
A similar explanation holds for the perception of the diamond shaped stimulus shown in Figure 20 A, which can be perceived as a square viewed obliquely in depth. Again, the stimulus is inverse-projected to a diamond cross-section extrusion shown in Figure 20 B. This extruded surface contains embedded within it an infinite array of irregular quadrilaterals with sides at various orientations in depth. But of those infinite possibilities, there is one special case in which the diamond is interpreted as a perfect square viewed obliquely, as suggested in Figure 20 C, or alternatively as another equally regular square tilted the other way in depth (not shown).
The “top-down” reflections from detected centers of symmetry are the mechanism that specifically picks out and enhances the most regular interpretations, relative to alternative less regular ones that receive no such support. This is how a field theory principle can search through an infinite range of spatial interpretations, and immediately pick out the most regular one from among them.

Figure 20 A: A two-dimensional stimulus of a diamond shape. B: The inverse-projection of the diamond, with shaded planes at the medial axes, and one central axis of higher order symmetry (dashed line). C: The perceptual interpretation of the stimulus as a perfect square viewed in perspective, as one of two alternative square percepts embedded in the inverse-projection of the stimulus.
A key principle of perceptual computation revealed in these simple figures is that the visual system does not jump to conclusions based on local stimulus evidence, but rather it attempts to remain in as general a state as is reasonably permitted by the stimulus, so as to allow as many alternative interpretations as possible for the particular stimulus. While the elliptical stimulus of Figure 18 A, and the diamond stimulus of Figure 20 A are bistable, or even tri-stable percepts (they can also be viewed as plane figures in the plane of the page), the addition of extra features to these stimuli reduce the number of reasonable alternatives, and the percept becomes fully stable in a single state.
For example the addition of a few extra features, as in Figure 21 A and D, stabilizes the percept to a single perceptual interpretation, as suggested in Figures 21 C and F respectively. The inverse projection of these figures shown in Figure 21 B and E, contain within them an infinite range of different interpretations, but the inverse-projections also contains embedded within them the regular cylindrical, and cubical interpretations, respectively, also, where they are detected and enhanced by symmetry detection and completion processes.

Figure 21 A and D: Two-dimensional stimuli. B and E: Inverse-projection of the respective stimuli. C and F: The volumetric interpretations that we tend to perceive, as a can and a box respectively, are embedded within the inverse-projection where they are detected and enhanced by their intrinsic symmetry.
Another significant feature of this principle of computation is that the symmetry detection and reification computations automatically recreate not only the exposed surfaces of the perceptual interpretation, but they also construct full volumetric effigies of the percepts they represent, a volumetric cylindrical and cubical object respectively, completing the form even through its hidden rear surfaces, as suggested by the dotted lines in Figure 21 C and F. This is amodal perception in three dimensions. When we see a regular object, like a ball on the beach, or a paint can in a hardware store, we see not only its exposed front surfaces, but we perceive the can as a volumetric cylinder, and we can easily reach back to its hidden rear surfaces and predict the exact depth and surface orientation of each point on those hidden surfaces, based only on the perceived configuration of its exposed faces.
3.8 Emergence, Complexity, and Invariance
Some of the most baffling aspects of perception identified by Gestalt theory, such as the perceptual emergence of global structure from fantastically complex and chaotic natural scenes, and the invariance of perception to rotation, translation, scale, and perspective or deformation, at least for simple shapes, can all be explained by the parallel spatial field-like nature of the computational algorithm of perception. The parallel nature of the computation means that it is no faster to calculate the medial axis of a cylinder than it is to calculate the axes of a hundred cylinders simultaneously. While human perception is clearly limited to some extent in the number of features that can be processed simultaneously, the experience of complex ornamental patterns like that shown in Figure 22 clearly demonstrate that the visual system is capable of considerable parallel perceptual computation, and to the degree that the visual system is demonstrably capable of parallel computation, that degree of parallel computation is explained by a parallel computational principle.

Figure 22. An ornamental pattern in which dozens of features are processed simultaneously and in parallel, to produce a near-instantaneous percept of a full volumetric form, including an acute awareness of the shape of the hidden rear surfaces perceived amodally.
The principle of perceptual reification of every possible interpretation at every location, orientation, and spatial scale simultaneously, in turn accounts for the invariance in perception, or the way that basic patterns, such as cylinders and helical spirals, are recognized immediately and pre-attentively in a visual scene containing possibly hundreds of individual forms, and that recognition is independent of the location, orientation, and scale of the perceived forms. But the fact that perception is invariant to translation, rotation, and scale, does not mean that perception is blind to those variations, as is often assumed. Although the bottom-up recognition of objects like cylinders and spirals is invariant to translation, rotation, and scale, the top-down reification of the hidden or occluded portions of those perceived forms occurs in a manner that is sensitive to the specific location, orientation, and scale of each perceived object where it lies in the visual field. Recognition is invariant to translation, rotation, and scale, but perceptual reification of those recognized forms is not.
The parallel nature of the computation also ensures that local symmetries will be detected even when in violation of the global pattern of symmetry. For example the same flame front propagation that discovers the central symmetry axis of a cylinder, as shown in Figure 21 A, will also find the central symmetry axis of a curvy cylinder, even one whose radius varies along the cylinder, as shown in Figure 22, because the local symmetry of the circular cross-section is preserved through the global curving of the central axis into a non-cylindrical form. The central axis is perceived as a curve, instead of a line.
If the central axis of a deformed cylinder takes on a larger pattern of regularity or symmetry, for example to define a full circular torus, or a figure 8 as in Figure 22, the visual system immediately picks up on such larger compound patterns of symmetry, or symmetry of symmetries, where the global pattern is observed to modulate the local symmetry, just as the local symmetry modulates itself to conform to the global pattern. In Figure 22, the helical curve of the black spiral modulates its basic cylindrical form, just as the cylinder modulates the helical curve, to create a compound helical-cylindrical form that is neither strictly helical nor cylindrical. The fact that people can both recognize, and perceptually complete such compound patterns is very significant, because it indicates that the primitives of geometrical representation in the brain are not rigid prototypes such as a Euclidean cylinder or cube, as suggested in the geon theory of spatial representation (Biederman 1987), but they are flexible adaptive templates that can modulate each other to create new compound concepts on the fly, such as a helical cylinder built up out of the more elemental cylindrical and helical primitives.
This principle explains the perception of the volumetric worm, in Figure 1 B. Although it is difficult to trace back the flow of the computation as we did for simpler figures, the very fact that the inverse projection of the stimulus of Figure 4 A contains within it the pattern of the experience in Figure 4 B, guarantees that that particular perceptual interpretation will get top-down support, whatever other patterns might be in there too. It does not matter that the worm’s cylindrical body is twisted into a spiral, it still has circular symmetry at every point along that spiral axis, and thus the spiral axis will itself reinforce that interpretation top-down. And if the worm’s central axis forms a regular spiral around the axis of the larger cylinder, that creates a higher order regularity at that cylindrical center, which will also reflect back out again to support that interpretation. Like an echo chamber that instantly picks out it resonant frequency from a white noise stimulus containing all frequencies, the visual system resonates to volumetric spatial interpretations that exhibit the most symmetry. It is not a piecemeal or sequential process of extracting first edges, then surfaces, and finally volumes, as has often been suggested, but rather, the entire process occurs simultaneously and in parallel, matching at the elemental and the global levels and every intermediate level simultaneously and in parallel, as suggested by Gestalt theory. While the reverse shock scaffolds algorithm cannot account for this kind of compound symmetry completion without some significant extensions or modifications, it remains an observational fact that such compound symmetries are detected in stimuli, and they are detected automatically and pre-attentively in a very short time, suggesting a low-level parallel computational process similar in at least some aspects to the forward and reverse shock scaffold concept.
4 Neurophysiological Considerations
Gestalt theory has played a significant role in theories of perception, mostly to counter simplistic theories of visual processing in terms of the detection of abstract features. The vivid spatial illusions introduced by Gestalt theory make it no longer reasonable to deny the existence of volumetric spatial percepts in our experience. Unfortunately Gestalt theory has not served well as a motivation for computational or neurophysiological theories of perceptual processing, chiefly because the elements of neurocomputation, spiking neurons and chemical synapses, appear to be the wrong type of representation to express the holistic emergent field-like aspects of perception that have defied characterization in objective, quantifiable terms. Many today unfortunately view Gestalt theory as a vague holistic concept that tells us nothing concrete about what’s going on in the brain. But maybe the problem is not with Gestalt theory, but with modern neuroscience. We have yet to identify the foundational principles behind the representation in the brain, or how it actually encodes the visual shapes that we experience, or even whether the brain goes to the trouble of constructing an explicit “virtual reality” representation of the world. Perhaps the real message of Gestalt theory is that our understanding of the foundational principles of neuroscience is fundamentally in error. Perhaps the significant aspect of neurocomputation is not spiking neurons communicating discrete signals along well defined processing paths gated by chemical synapses. Perhaps there is an entirely different paradigm of computation taking place in the brain, an emergent field-like spatial computational principle taking place in a spatial medium, to create a complete holographic world of our experience. Perhaps the atomistic view of neurocomputation offered by the neuron doctrine (Barlow 1972, 1995) has been holding up progress in understanding the computational principles of perceptual processing.
In fact the problems with the Neuron Doctrine date as far back as the development of the first brain recording technique, the electroencephalogram (EEG). From the outset the EEG detected a global oscillation across the whole brain, and that global synchrony was found to correlate with particular functional states. However the significance of this global resonance remains to this day as mysterious as it was when it was first discovered. Now with the introduction of multiple-unit recordings, this global resonance is even beginning to manifest itself in electrophysiological data. Although it is not much discussed in the contemporary literature, this kind of global resonance is problematic for the Neuron Doctrine. For the phasic spiking of a neuron is unlikely to survive across the chemical synapse, due to the multiple parallel paths in each axonal and dendritic arborization, each with variable path lengths and dendritic diameters which would introduce random time delays across all those parallel paths, not to mention the temporal averaging of the signal in each of the 10,000 or so parallel chemical synapses that connect a typical pair of neurons. After the third or fourth such transmission along a line of cells, the phasic pulses of the neural signal would surely diffuse into a featureless blur, which would preclude the kind of global synchrony observed in the EEG signal across the cortex as a whole.
Another Achilles heel in the Neuron Doctrine that receives little mention today, is the fact that the cell membrane, although capable of insulating electrical charge inside the cell, does not insulate alternating currents. For like the insulating dielectric in a capacitor, the cell wall transmits alternating current signals perfectly well, and blocks only direct current. That is why single-cell electrode recording can be performed extra-cellularly, just as well as intra-cellularly. This in turn suggests that the alternating current spiking signal of the neuron is likely to propagate directly from cell to cell across the extracellular matrix, unhindered by the insulation of the cell membrane, except in mylenated axons. Pribram (1971) proposed that the overt spiking of the neuron is not the causal origin, but merely a secondary manifestation or response of the cell to a graded potential oscillation that pervades the body of neural tissue, because that oscillation has been observed to continue even after the spiking cell falls below threshold and ceases to fire. Like whitecaps on ocean waves, the spiking neuron merely reveals the presence of a more subtle underlying resonance that pervades the bulk neural tissue. The reason that this graded potential oscillation has received so little attention in electrophysiological circles has been for lack of a theoretical framework to give meaning to those resonances, or to explain how harmonic resonance can perform a computational function in the brain.
I propose that the global synchrony observed in the EEG recordings, and now in the synchronous activity of cortical neurons, is exactly what it appears to be, i.e. it is a manifestation of a global harmonic resonance that pervades the entire cortex, and that this resonance subserves a computational function which is central to the principle of operation of the brain (Lehar 1994a, 1994b, 1999a, 1999b, 2003a, 2003c). The purpose of this resonance is to set up a pattern of standing waves, and these standing waves serve a function which is normally ascribed to spatial receptive fields in neural network models, i.e. as a mechanism for encoding spatial patterns in the brain both for recognition and for perceptual completion. This theory has already explained a host of illusory vertex perception phenomena that are difficult to account for by other means (Lehar 2003c).
5 Phase Conjugation
Harmonic resonance is a linear wave phenomenon. There is a very interesting phenomenon observed in nonlinear optics called phase conjugation, that just happens to mirror some of the reconstructive properties of perceptual reification. In fact, a nonlinear standing wave model exhibits many of the properties of a forward-and-reverse grassfire algorithm cycling repeatedly between abstraction and reification half-cycles. I propose that phase conjugation is the computational principle behind perceptual reification by symmetry completion. Since phase conjugation is an exotic phenomenon with which few psychologists or neurophysiologists have much familiarity, I present a brief summary of the essential principles of phase conjugation in the appendix for interested readers, and provide a more informal intuitive sketch of the relevant concepts here.
In linear optics, light waves pass through each other transparently, as if the other waves were not there, and the same is true of the ripples on a pond that also pass through each other totally unaffected after they cross. But almost any optical, or other wave phenomenon, will go non-linear if the amplitude is sufficiently high, and that is also true of water waves, to help our intuition. When waves in a ripple tank are driven too strongly, they lose their perfect sinusoidal shape, and form sharper peaks between wide valleys, like wind-driven waves on the ocean. A most extreme nonlinear wave is seen in breaking waves on the beach, whose towering crests carry with them a slug of moving water. Waves of this sort do not pass through each other transparently, but they collide and rebound energetically like colliding billiard balls. In reality, nonlinear waves exhibit both linear and nonlinear components, so that colliding waves will simultaneously pass mostly through each other unaffected, and at the same time some portion of those waves collide with, and rebound off each other, creating reflections in both directions. This concept of waves colliding and rebounding provides the key insight into understanding the otherwise mysterious phenomenon of phase conjugation.
Figure 23 illustrates the behavior of a phase conjugate mirror compared to a regular mirror. Like a conventional mirror, a phase conjugate mirror reflects incident light back out again. But unlike a regular mirror, the reflected ray travels back exactly in the direction from whence it came, as a time-reversed replica of the original incoming ray. Intuitively, this process can be understood by analogy with physical collisions and rebounding by billiard balls. The reflecting element in the phase conjugate mirror is a standing wave interference pattern caused by intersecting laser beams in a block of nonlinear optical material. When an incident ray of light strikes this standing wave interference pattern from any angle, most of the ray passes straight through the standing wave unchanged, but a portion of it is reflected back in the direction that it came from, as if rebounding from an elastic collision with the standing wave. This antiparallel rebounding of a ray of light in nonlinear optics, along with Huygen’s principle of wave propagation, are sufficient to explain some of the bizarre time-reversed reconstruction principles in phase conjugation, which is the principle that mirrors an observed property of perceptual reification.
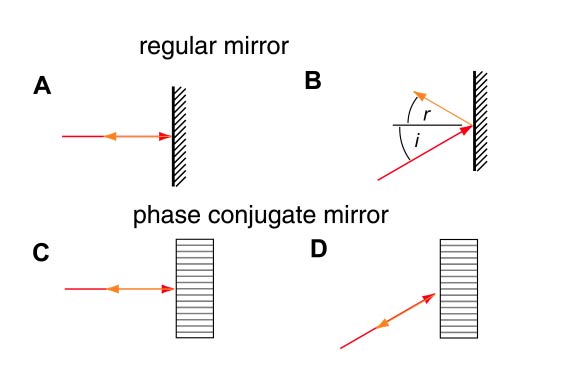
Figure 23 A and B: A conventional mirror reflects light out such that the angle of reflection is equal to the angle of incidence. C and D: A phase conjugate mirror reflects light back out in the direction from whence it came, as a time-reversed reflection of the original wave.
For example one of the most remarkable feats performed by phase conjugation is the ability to undo an optical distortion by passing the image backwards through the same device that produced the distortion in the first place. Since every ray reverses its path exactly through the distorter, the distortion is automatically undone in the reverse pass. Figure 24 A shows a coherent beam of light passed through a warped distorting glass that scatters the rays in random directions. B: After reflection in a regular mirror, the beam is scattered more on its second pass through the distorting glass. Figure 24 C shows the same scattered beam, this time striking a phase conjugate mirror. D: The mirror reverses every ray individually, causing it to retrace its path through the optical distorter, which completely undoes the distortion, and restores the original coherent beam, amplified, and traveling in the opposite direction. This technique can be used, for example, to amplify a light image using the phase conjugate mirror, without introducing any of the distortions along the light path.

Figure 24 A : A coherent laser beam is sent through a distorting glass that scatters the light rays randomly. B: After reflection in a conventional mirror, the rays get scattered more in their second pass through the optical distorting glass. C: The same arrangement except this time using a phase conjugate mirror. D: The mirror reverses each ray exactly, which makes it follow its path through the distorter in reverse, thus undoing the scattering of the distorting element.
5.1 Huygen’s Principle
Huygen’s principle states that a wave front is mathematically equivalent to a line of point sources all along that front, because the outward-radiating rays from adjacent point sources along the front eventually cancel by destructive interference, leaving only the component traveling in a direction normal to the local orientation of the front. This important principle is implicitly present in the grassfire analogy: the flame front always advances in a direction normal to the local orientation of the front. This principle has an interesting spatial consequence, that if the flame front has a shape, whether curved convex or concave, or a zigzag or wavy line pattern, the shape of that wave front has a profound influence on the pattern of propagation of that front.
Figure 25 A shows an opaque white painted sphere illuminated by coherent light from a collimated laser beam. The light striking the opaque surface is absorbed and re-emitted from the surface as from innumerable point sources that generate coherent wave fronts propagating outward normal to the surface in expanding spherical shells. The light passes through a half-silvered mirror at Figure 25 B, and on to a phase conjugate mirror at Figure 25 C, where the diverging pattern of light rays is reflected back out as converging rays. A portion of the converging rays are reflected by the half-silvered mirror down to Figure 25 D, where a virtual sphere is reconstructed about the center of symmetry where the converging rays meet at the virtual center. This demonstrates how a phase conjugate mirror tends to reconstruct centers of symmetry. Now if we could only arrange to have the virtual sphere appear within the phase conjugate mirror instead of outside it, the high amplitude converging wave fronts would tend to trigger an outward reflection back out from the symmetry center, as suggested by the faint expanding wave fronts shown in Figure 25 D.

Figure 25. A : An opaque white sphere illuminated by coherent light, generates coherent wave fronts propagating outward in spherical shells from the surface. The expanding rays are reflected back inward by C: a phase conjugate mirror, that creates spherical wave fronts converging on a focal point. A portion of these rays is reflected by B: a half-silvered mirror, to create D: a virtual sphere about a center of spherical symmetry. If this process could be contrived to occur inside a phase conjugate mirror, it would project an outward-propagating reconstruction of the whole sphere, as suggested by the faint concentric arcs.
5.2 Perceptual Reification by Phase Conjugation
Figure 26 shows a possible arrangement for performing perceptual reification using a phase conjugate mirror. (See the appendix for a summary of the principles of phase conjugation) The mirror is set up by two powerful pumping beams, B1 and B2 that propagate in opposite directions to create a nonlinear standing wave throughout the volume of the nonlinear optical element, indicated by the rectangular solid in the figure. A powerful illumination source, for example a collimated strobe light, is projected through a slide transparency that holds the two-dimensional stimulus image in outline form, as in an edge image. The example stimulus in Figure 26 is an ellipse, as a transparent outline on an otherwise opaque slide. This arrangement inverse-projects an elliptical cylinder of light into the volume of the phase conjugate mirror. The strobe light is bright enough to raise a significant fraction of the electrons in the nonlinear medium to higher energy levels, as in conventional laser pumping, from which they will tend to decay spontaneously, producing rays in all directions emitted from within the surface of the elliptical cylinder. By Huygens’ principle, this sudden release of energy throughout the surface of the elliptical cylinder will trigger wave fronts propagating inward and outward, normal to the surface of the elliptical cylinder, like a shock scaffold algorithm. The wave fronts that radiate outward from the elliptical cylinder get dispersed with distance, and thus tend to fade. But the wave fronts radiated inward toward the axis of the elliptical cylinder will be amplified as they converge towards the symmetry center, creating a region of high amplitude within the plane surface of the medial axis of the elliptical cylinder, as suggested by the gray shaded patch in the figure. At the center of that patch, along the exact axis of the elliptical cylinder, is the locus of the centers of the tilted circles that are embedded in the surface of the elliptical cylinder, and thus one would expect extra high amplitude convergence along that singular line, as indicated by the darker shading. If the amplitudes are adjusted such that phase conjugation occurs along these axes of symmetry, that would promote a phase conjugate reflected wave to reflect back outward from that central axis to specifically reify those regions in the elliptical cylindrical surface that correspond to the perfect circular interpretations of the elliptical stimulus. Unlike a regular phase conjugate mirror, (see the appendix) the fourth beam B4 never leaves the phase conjugate mirror, but remains trapped inside it, resonating back and forth, inward and outward between the percept embedded within the extruded surface, and its points of volumetric symmetry in the computational matrix.

Figure 26. A : A possible configuration for perceptual reification using phase conjugation. Anti-parallel pumping beams B1 and B2 create a phase conjugate mirror within the volume of the nonlinear optical element, indicated by the rectangular solid. A two-dimensional stimulus image is illuminated by a collimated strobe light, to create an inverse-projection of the stimulus in the volume of the phase conjugate mirror. The stimulated emission within the surface of this extruded ellipse in turn promotes waves that propagate normal to the stimulated surface, that converge on the medial axis skeleton of the volumetric form. Phase conjugation within this medial axis skeleton reflects this converging wave back out again, to reinforce or amplify those aspects of the extruded stimulus that were responsible for the symmetry peaks.
Phase conjugation also provides a mechanism for the “print” function outlined above, whereby the outward-propagating wave front is abruptly frozen in space after a time delay equal to the time delay of its inward convergence to the symmetry center. Whereas the shock scaffold algorithm is a single-pass process, phase conjugation is a cyclic affair, and the period of the cycle is determined by the size of the perceived object, while the waveform of the cycle is determined by its shape. This means that the quantity referred to above as the time delay, whether bottom-up in perception or top-down in reification, can now be seen as the time delay within each cycle, or the frequency of oscillation. For example the inward convergence from a spherical surface to its spherical center and back out again to the surface, would cycle faster for a smaller sphere than for a larger one due to the shorter radial distance.
The entire cycle of perception and reification can now be explained in terms of local oscillators distributed throughout the computational matrix that detect, and resonate to periodic oscillations by oscillating in phase with them. The cycle begins with the perceptual input, that projects a two-dimensional stimulus into the volumetric perceptual matrix. Oscillators that are embedded within the inverse-projected surface of the stimulus record a powerful non-coherent wave arrival at time zero, which triggers them to emit an omni-directional pulse immediately, and the collective emission from all points within the extruded surface creates wave fronts that propagate normal to the surface by Huygens’ principle. Oscillators located at points outside the extruded surface receive a series of weaker wave fronts after time delays proportional to the distance of the oscillator from each emitting surface. If an oscillator is located on a point or a line of symmetry, it will receive a more powerful pulse from different directions simultaneously, which raises that point in the matrix into the nonlinear regime, causing that point to emit an omni-directional pulse from its location immediately. When the pulse from the symmetry center arrives back out at the extruded surface, it will preferentially stimulate those points in the surface that contributed the most to the symmetry response, for example the tilted circles embedded within the elliptical extrusion. This top-down pulse in turn triggers the those points in the extruded surface to emit an omni-directional pulse again, and the cycle repeats, resonating to the bottom-up / top-down matching between the perceived surfaces and their centers of perceived symmetry. The timing of the “print” phase to freeze the outward-propagating wave as it reaches the extruded surface is thus provided by the temporal synchrony between the points within the perceived surfaces and their detected centers of symmetry. As the synchrony is established, the percept starts pulsing in anti-phase with the pulsing of its symmetry center, at a frequency that is proportional to the size of the percept in the representation.
6 Discussion
The theory of vision presented herein may seem somewhat vague and ill-specified as a computational model of perception. That is why the theory is presented not as a model of visual perception by phase conjugation, nor even by a forward-and-reverse grassfire or shock scaffold algorithm, because there is neither sufficient evidence for those exact algorithms in perception, nor are those algorithms sufficiently specified to be a perceptual model in the usual sense. Instead, the primary message of this paper is more general, and it comes at several levels with various degrees of certainty at each level. First and foremost, the message of this paper is that visual perception has a constructive, or generative function that constructs a complete virtual world of experience based on a relatively impoverished sensory input. The information content of that world of experience is equal to the information content of a painted model world, like a diorama, or a theater set, with volumetric objects bounded by colored surfaces embedded in a spatial void. In other words, the representational strategy used by the brain is an analogical one. That is, objects and surfaces in the world are represented in the brain not by an abstract symbolic code, as suggested in the propositional paradigm of Artificial Intelligence, nor are they encoded by the activation of individual cells, or groups of cells representing particular features in the scene, as suggested in the neural network or feature detection paradigm. Instead, objects are represented in the brain by constructing full spatial effigies of them that appear to us for all the world like the objects themselves—or at least so it seems to us only because we have never seen those objects in their raw form, but only through our perceptual representations of them.
The computational processes of visual perception are also explicit spatial field-like processes, as we see in the case of Gestalt illusions. Whether perception employs anything like a reverse grassfire or shock scaffold or phase conjugate type algorithm, the effect of visual processing clearly exhibits properties as if perception were using some kind of reverse shock scaffold type principle in perceptual reification, in which central symmetries that are detected in the stimulus are interpolated and/or extrapolated back out again to produce an explicit volumetric structure in experience with both modal and amodal components, as the simplest, most geometrically regular structural interpretation of configuration in the world that is most likely to have been the cause of the given visual stimulus. This computational process is real, and demands a neurophysiological explanation.
A common objection to the notion of explicit filled-in pictorial representations in the brain is that explicit representations are not necessary, because pictorial information can be encoded in an abstracted, non-pictorial code. While this may be true strictly speaking, in the case of explicitly spatial algorithms, like a grassfire or shock scaffold algorithm, there is a considerable cost incurred by computing a massively parallel spatial algorithm in a discrete sequential symbolic or abstracted computation, and that cost increases exponentially the more massively parallel the algorithm. The fact that visual perception routinely solves the inverse optics problem, and does so effortlessly and virtually instantaneously, and does so even in the case of complex stimuli composed of hundreds or thousands of visual features as in a natural scene, strongly implicates a parallel computational algorithm in perception. Whether the reverse shock scaffold algorithm can be specified so as to make more detailed quantitative predictions of specific perceptual phenomena remains to be seen. But one thing the reverse shock scaffold algorithm clearly demonstrates is the principle of spatial reification, and how it is possible to search a virtually infinite space of possible interpretations in a finite, almost instantaneous time with the right kind of parallel feedback algorithm. This opens the possibility for practical solutions to the inverse optics problem, a problem that has been generally considered to be computationally intractable.
As for the concept of phase conjugate mirrors as a principle of computation in the brain, that is the most speculative and uncertain part of the present proposal. It is not even clear whether the system depicted above in Figure 26 would even function as advertised. The computational concepts outlined above would have to be investigated in nonlinear optical experiments, and nonlinear standing wave phenomena would have to be identified neurophysiologically, before phase conjugate mirrors could be advanced as a serious theory of neurocomputation. But the experiments would never be conducted, and the neurophysiology would never identified, if there were no motivation to seek out those principles in optical and neurophysiological experiments. In fact, there may already be plenty of evidence in support of phase conjugation in the brain, if only people knew to look out for such evidence. The principal motivation of the present paper is to inspire nonlinear optical researchers and neurophysiologists alike to seek confirmation of nonlinear wave phenomena in the brain if it is in there. You have to know what you are looking for if you are to have any chance of finding it. But whether or not phase conjugation is an important computational principle in the brain, it is both interesting and significant that nonlinear wave phenomena and phase conjugation are common, even if generally unfamiliar, in the physical world, and it is both suggestive and compelling that such a simple physical principle exhibits such exquisitely complex and elaborate computational properties, properties which had hitherto been considered to be computationally intractable. Whether or not nonlinear phase conjugation is an essential aspect of perceptual computation, phase conjugate mirrors are a fascinating concept of parallel computation that is useful to bear in mind when seeking massively parallel field-like computational paradigms to account for the extraordinary capacities of visual perception.
I close with a quote from Ramachandran & Blakeslee (1998, p. xv).
I'd also like to say a word about speculation, a term that has acquired a pejorative connotation among some scientists. Describing someone's idea as "mere speculation" is often considered insulting. This is unfortunate. As the English biologist Peter Medawar has noted, "An imaginative conception of what might be true is the starting point of all great discoveries in science." Ironically, this is sometimes true even when the speculation turns out to be wrong. Listen to Charles Darwin: "False facts are highly injurious to the progress of science for they often endure long; but false hypotheses do little harm, as everyone takes a salutory pleasure in proving their falseness; and when this is done, one path toward error is closed and the road to truth is often at the same time opened."
Appendix
7 The Principles of Nonlinear Phase Conjugation
Not many psychologists or neuroscientists are likely to be familiar with nonlinear optics and phase conjugation, so a brief intuitive introduction is provided to cover the principal concepts. More rigorous treatments can be found in Boyd (2003) and Fisher (1988). Although this description is presented using examples from laser optics, the key concepts apply to nonlinear resonances that can often be found most anywhere that linear resonances are found.
7.1 Linear and Nonlinear Optics
The key difference between linear and nonlinear wave phenomena is that linear waves pass through each other transparently, as if the other wave did not exist, whereas nonlinear waves collide more like physical objects, rebounding back a portion of the wave by reflection after collisions with other waves. This can be seen in the phenomenon known as four-wave mixing, (Boyd 2003, Fisher 1983) in which three laser beams intersect in a nonlinear optical medium, creating an additional beam by diffraction. We begin by examining the effect of mixing just two beams. Figure A1 A shows two laser beams, B1 and B2, that intersect through some volumetric region of space. In the volume of their zone of intersection, a pattern of standing waves emerges in the form of parallel planes, oriented parallel to the bisector of the angle between the two beams, as shown in Figure A1 A. This interference pattern due to the intersection of nonlinear wave fronts is analogous to the formation of a shock scaffold at the angular bisector between the intersecting wave fronts depicted in Figure 19 A, except that the waves do not only collide along the central plane of the medial axis, as in a shock scaffold algorithm, but they form a number of parallel planes whose spacing varies with the wavelength, and the angle between the beams. Figure A1 B shows in two dimensions how the wave fronts from the two beams intersect to produce high amplitude by constructive interference along the vertical lines in the figure, interleaved with planar nodes of low or zero amplitude in between, due to destructive interference.

Figure A1 A: Two laser beams B1 and B2 that cross, create an interference pattern in their zone of intersection. B: Constructive interference creates a pattern of high amplitude in parallel planes, parallel to the angular bisector of the two beams, with planes of low amplitude in between. C: The wave vector diagram for the crossing beams, including a new lattice vector KL that corresponds to the difference vector between the crossing beams.
In linear optics this interference pattern is a transient phenomenon that has no effect on anything else. However if the crossing of laser beams occurs in the transparent volume of a nonlinear optical medium, as suggested by the rectangular block in Figure A1 A, and if the amplitude of the beams is sufficiently large, the interference pattern will cause a change in the refractive index of the nonlinear medium in the shape of those same parallel planes, due to the optical Kerr effect. The alternating pattern of higher and lower refractive index in parallel planes behaves like a Bragg diffractor.
7.2 Bragg Diffraction
Bragg diffraction is distinct from regular diffraction by the fact that the diffracting element is not a two-dimensional grating of lines etched on a flat sheet, as in standard diffraction, but a solid volume containing parallel planes of alternating refractive index. Bragg diffraction was first observed in x-ray crystallography as a sharp peak of reflection at a particular angle of incidence to the crystal lattice planes. The crystal layers behave much like a stack of partially-silvered mirrors, each plane passing most of the light straight through undiminished, but reflecting a portion of that light like a mirror, with the angle of reflection equal to the angle of incidence. However because of interference between reflections from successive layers at different depths, Bragg diffraction is stronger at those angles of incidence that promote constructive interference between reflected rays, but weakens or disappears altogether at other angles where the various reflected beams cancel by destructive interference. Maximal diffraction occurs at angles that meet the Bragg condition, that is,
2 d sin q = n l
where q is the angle of the incident ray to the plane of the reflecting surface, d is the distance between adjacent planes, l is the wavelength of light, and n is an integer. In words, Bragg reflection occurs at angles of reflection where the path length difference between reflections from adjacent planes differ by an integer number of wavelengths.
7.3 Reciprocal Lattice Wave Vector Representation
The phase matching constraint enforced by the Bragg condition can be seen most easily in a Fourier space called the reciprocal lattice representation. Each beam is represented by a wave vector whose direction is normal to the wave fronts of the corresponding beam, and whose magnitude is proportional to the inverse of the wavelength, or spacing between successive wave fronts of the beam. This is a Fourier representation in that the magnitude of the wave vectors is proportional to the frequency of the corresponding wave. Mathematically, the magnitude k of the wave vector of a wave of wavelength l is given by
k = 2p / l
The convenience of this representation is that the wave vectors of waves that are phase matched so as to be in a mutually constructive relationship, form closed polygons in this space, and this can be used to determine whether the Bragg condition is met.
Figure A1 C shows the wave vector representation for the crossing laser beams depicted in Figure A1 A. The wave vectors K1 and K2 are oriented parallel to their corresponding beams B1 and B2. The parallel planes of a Bragg diffractor, such as a crystal composed of parallel planes, can also be expressed as a wave vector because it behaves very much like a beam of coherent light to an incident beam that strikes it. As with wave vectors, the direction of this lattice vector KL is normal to the planes of the grating, and the vector magnitude is proportional to the inverse of the spacing between lattice planes. Figure A2 A shows the nonlinear optical element replaced by a functionally equivalent crystal with lattice planes parallel to those of the standing wave. The vector diagram of Figure A1 C shows the lattice vector KL that would be required for the phase matching relation dictated by the Bragg condition to hold. In terms of wave vectors in the reciprocal lattice representation, the Bragg condition holds when
K1 + KL = K2,
or equivalently,
K2 - KL = K1.
The lattice vector acts in opposite directions on K1 and K2, which is why it is added to one but subtracted from the other. Note how the lattice vector is oriented normal to the planes of the lattice, which are parallel to the angular bisector of the two beams, as required for the angle of incidence to equal the angle of reflection. For example if the lattice spacing were somewhat larger than that dictated by the Bragg condition, that would make the lattice vector shorter, and the three vectors would no longer form a closed triangle, and thus little or no Bragg refraction would be expected to occur with that crystal, that is, the light would pass through with little or no reflection. Bragg refraction could be restored, however, by re-aligning either or both beams to make their wave vectors meet the shorter lattice vector.

Figure A2. A: Nonlinear optical element replaced by functionally equivalent crystal with lattice planes parallel to the original standing waves, and with the same spacing as the standing waves. B: If beam B2 were shut off, then beam B1 together with the crystal would recreate B2 by Bragg diffraction. C: Conversely, if beam B1 were shut off, then beam B2 together with the crystal would recreate B1 by Bragg diffraction.
7.4 Magical Reification
The magic of nonlinear optics is that when laser beams cross in the volume of a nonlinear optical medium, as depicted in Figure A1 A, the wave vector of the resultant nonlinear standing wave pattern automatically takes on the configuration required by the Bragg condition, no matter what the angle of intersection of the two beams. So although Bragg reflection occurs off a crystal only for certain specific angles that meet the Bragg condition, laser beams that cross in a nonlinear optical medium create a standing wave whose lattice vector is automatically equal to the difference between the two crossing beams, or,
KL = K2 - K1.
This is the constructive, or generative function of nonlinear optics that is ultimately responsible for reification in perception. If the pattern of standing waves were somehow frozen as a fixed pattern of alternating refractive index, as in a layered crystal, as suggested in Figure A2 A, then this crystal would behave like a hologram that can restore the pattern of light if one of the input beams is removed. For example Figure A2 B shows beam B1 refracted by the functionally equivalent crystal lattice to produce a reflected beam in the direction of the original beam B2, and Figure A2 C shows beam B2 refracted by the equivalent crystal lattice to recreate the original beam B1. The reification in two-wave mixing has created a difference vector that has created a redundancy in the representation that allows either one of the input signals to be removed without loss of information.
The nonlinear standing wave establishes an energy coupling between the two intersecting waves, such that one wave can “pump” or amplify the other. For example if B1 is of higher amplitude than B2, then the interference pattern between B1 and B2 reflects some of the energy of B1 in the direction of B2, as in Figure A2 A, whereas if B2 is of higher amplitude than B1, some of the energy of B2 is reflected in the direction of B1, as in Figure A2 B. In fact, whether the two beams are of equal amplitude or not, some portion of B1 is always lost to B2 through the crystal, while some portion of B2 is lost to B1, as suggested in Figure A2 A, so the net energy transfer always flows from the higher amplitude beam toward the lower. That is, the two waves are intimately coupled through the nonlinear standing wave, energy-wise, and this energy coupling is what allows phase conjugation to produce an amplified reflection.
7.5 Enter the Third Beam
Now we will add a third probe beam, B3, to intersect with the other two beams in the nonlinear optical element as shown in Figure A3 A. This creates a fourth signal beam B4 which will eventually be our phase conjugate beam after one last modification. The direction of that fourth beam can be computed from the vector diagram shown in Figure A3 B, by the principle that the fourth beam will exactly cancel or balance the sum of the other three vectors, or,
K1 + K2 + K3 + K4 = 0.
Again, this is dictated by the phase matching constraint, whereby the only waves that will emerge are those that reinforce each other constructively, and the reciprocal wave vector diagram helps identify the conditions under which that constraint is met. If the pumping beams K1 and K2 remain fixed, then whichever way the probe beam wave vector K3 is directed from the point (K1 + K2) in the vector diagram, the conjugate beam will always return back to the origin, as shown in Figure A3 B.
There are two ways that this phenomenon can be understood intuitively. We can say that probe beam B3 interferes with pumping beam B1 to produce an interference pattern as shown in Figure A3 C along their angular bisector, then beam B2 reflects off that interference pattern to produce the signal beam B4. (angle of reflection equals angle of incidence) Alternatively we can say that the probe beam B3 interferes with other pumping beam B2 to produce an interference pattern as shown in Figure A3 D, then beam B1 reflects off that interference pattern to produce the signal beam B4. It is more accurate however to think of all four beams as interlocked in a four-way energy coupling consummated by the newly created signal beam that appears so as to balance the vector equation and maintain phase coherence between all four beams. In other words, both interference patterns of Figure A3 C and D, co-exist simultaneously along with the original pattern of Figure A1 A, interlocking the four beams in a mutually interdependent energy relation.

Figure A3. A: A third beam B3 is directed into the intersection of the other beams, which produces a fourth beam B4.The angle of that new beam can be calculated from the wave vector diagram as shown in B. This can be seen intuitively as C: an interference that forms between B3 and B1, followed by a reflection of B2 by that pattern to create B4, or alternatively it can be seen as D: an interference between B3 and B2, followed by a reflection of B1 by that interference pattern to create B3.
7.6 Phase Conjugate Mirror
All we need to do to complete the phase conjugate mirror is to orient beams B1 and B2 anti-parallel to each other, so that in vector terms K1 + K2 = 0. This in turn means that K3 + K4 = 0, which means that the reflected beam B4 must be the phase conjugate of the probe beam B3. Figure A4 A shows the configuration required for phase conjugation. Pumping beams B1 and B2 are projected into the nonlinear optical element from opposite directions where they interfere to form a nonlinear standing wave. The probe beam B3 can now be projected into the mirror from any direction, and this will produce the phase conjugate beam B4 superimposed on B3 but traveling in the opposite direction as a “time-reversed” reflection. The summation of B3 and B4 traveling in opposite directions converts the two waves into a standing wave that oscillates without propagation if they are of equal amplitude, otherwise there will be a net propagation in the direction of the higher amplitude beam. Figure A4 B shows the wave vector diagram showing how if K1 + K2 = 0, then K3 + K4 also equals 0 no matter what angle the probe beam enters the mirror, and thus B4 must be the phase conjugate of B3.
If the pumping beams are provided at high amplitude, then the energy built up in the nonlinear standing wave can spill over to the conjugate wave, creating an amplified reflection of the incoming wave back outward in the direction from whence it came. This is the phase conjugate mirror produced by degenerate four-wave mixing.

Figure A4. A: A phase conjugate mirror is produced by anti-parallel pumping beams B1 and B2 that cross in opposite directions in the nonlinear optical element. When a third probe beam B3 is projected into the mirror from any direction, a phase conjugate beam B4 will appear as a time-reversed reflection of the probe beam in the direction from whence it came. B: The wave vector diagram shows how if K1 + K2 = 0, then K3 + K4 also equals 0, and thus B4 must be the phase conjugate of B3.
8 References
Barlow H. B. (1995) The Neuron Doctrine in Perception. In M. Gazzaniga (Ed.), The Cognitive Neurosciences. Cambridge: MIT Press.
Biederman, I. (1987). Recognition-by-Components: A Theory of Human Image Understanding. Psychological Review, 94, 115-147.
Harry Blum (1973) Biological shape and visual science. Journal of Theoretical Biology, 38:205–287.
Boyd R. W. (2003) Nonlinear Optics. San Diego: Academic Press.
Coren S., Ward L. M., & Enns J. J. (1994) Sensation and Perception. Ft Worth TX, Harcourt Brace.
Cornsweet TN (1970) Visual perception. Academic, New York
Craik KJW (1966) The nature of psychology (Sherwood SL, ed). Cambridge, UK: Cambridge UP
Dennett D. C. (1992) `Filling In' Versus Finding Out: a ubiquitous confusion in cognitive science. In Cognition: Conceptual and Methodological Issues, Eds. H. L. Pick, Jr., P. van den Broek, & D. C. Knill. Washington DC.: American Psychological Association
Dupuis, G. & Berland, N. (2004) Belousov-Zhabotinsky, Encyclopedia of Nonlinear Science NL 3600, Alwyn Scott (ed), New York: Taylor and Francis .
Fisher, R. A. (1983, Ed) Optical Phase Conjugation. New York: Academic Press.
Gibson J. J. (1972) A Theory of Direct Visual Perception. In: The Psychology of Knowing. (J. R. Royce & W. W. Rozeboom (Eds.), Gordon & Breach.
Gibson J. J. (1979) The Ecological Approach to Visual Perception. Houghton Mifflin.
Grossberg S, & Mingolla E, (1985) "Neural Dynamics of Form Perception: Boundary Completion, Illusory Figures, and Neon Color Spreading" Psychological Review 92 173-211.
Grossberg S, & Todorovic D, (1988) "Neural Dynamics of 1-D and 2-D Brightness Perception: A Unified Model of Classical and Recent Phenomena" Perception and Psychophysics 43, 241-277.
Helson H. (1963) Studies on Anomalous Contrast and Assimilation. Journal of the Optical Society of America 53, 179-184.
Idesawa M. (1991) Perception of Illusory Solid Object with Binocular Viewing. Proceedings IJCNN
Koffka, K.(1935). Principles of gestalt psychology. New York: Harcourt Brace.
Köhler, W. (1924). Die physischen Gestalten in Ruhe und im stationären Zustand: Eine naturphilosophische Untersuchung. Erlangen: Verlag der Philosophichen Akademie.
Kuhn T. S. (1970) The Structure of Scientific Revolutions. Chicago: Chicago University Press.
Land E. H. & and McCann, J. J. (1971) "Lightness and Retinex Theory," Journal of the Optical Society of America, Vol. 61, No. 1, pp 1-11.
Lehar S. (1994a) "Directed Diffusion and Orientational Harmonics: Neural Network Models of Long-Range Boundary Completion through Short-Range Interactions". Ph.D. Thesis, Boston University. Available at .//webstuff/thesis/thesis.html
Lehar S. (1994b) "Harmonic Resonance in Visual Perception Suggests a Novel Form of Neural Communication. rejected Perception & Psychophysics 1995. Available at .//webstuff/pnp/pnp.html
Lehar S. (1999a) "Computational Implications of Gestalt Theory 1: A Multi-Level Reciprocal Feedback (MLRF) to Model Emergence and Reification in Visual Processing". Rejected Perception & Psychophysics October 1999. Rejected Cognitive Psychology November 2000. Available at
.//webstuff/orivar/orivar1.html
Lehar S. (1999b) "Computational Implications of Gestalt Theory 2: A directed diffusion to model collinear illusory contour formation". Rejected Perception & Psychophysics October 1999. Rejected Cognitive Psychology November 2000. Available at .//webstuff/orivar/orivar2.html
Lehar S. (2003a) "The World In Your Head: A Gestalt view of the mechanism of conscious experience." Mahwah NJ: Erlbaum. Additional information available at .//webstuff/book/WIYH.html
Lehar S. (2003b) "Gestalt Isomorphism and the Primacy of the Subjective Conscious Experience: A Gestalt Bubble Model". The Behavioral and Brain Sciences 26(4), 375-444. Also available at .//webstuff/bubw3/bubw3.html
Lehar S. (2003c) "Directional Harmonic Theory: A Computational Gestalt Model to Account for Illusory Contour and Vertex Formation". Perception 32(4) 423-448. Also available at
.//webstuff/dirhr1/dirhr1.html
Frédéric Fol Leymarie (2003) Three-Dimensional Shape Representation via Shock Flows. PhD thesis, Brown University, Providence, RI, USA, May 2003. URL: www.lems.brown.edu/~leymarie/phd
J. Hochberg and V. Brooks, The psychophysics of form: reversible - perspective drawings of spatial objects, American Journal of Psychology, vol. 73, 1960, pp. 337-354.
McLoughlin, N. (2003) Bursting the Bubble: Do we need true Gestalt isomorphism? Behavioral & Brain Sciences 26(4) 375-444.
Michotte, A., Thinés, G., & Crabbé, G. (1991). Amodal completion of perceptual structures. In G. Thinés, A. Costall, & G. Butterworth (Eds.), Michotte’s experimental phenomenology of perception (pp. 140–167). Hillsdale, NJ: Lawrence Erlbaum Associates. (Original work published in 1967).
O’Brien V (1959) Contrast by contour-enhancement. Am J Psychol 72:299–300
O'Regan K. J., (1992) Solving the `Real' Mysteries of Visual Perception: The World as an Outside Memory. Canadian Journal of Psychology 46 461-488.
Paradiso, M. A., & Nakayama, K. (1991). Brightness perception and filling-in. Vision Research, 31, 1221-1236.
Pessoa L., Thompson E., & Noë A. (1998) Finding Out About Filling-In: A guide to perceptual completion for visual science and the philosophy of perception. Behavioral and Brain Sciences 21, 723-802.
Pribram, K. H. (1971). Languages of the brain. New York: Prentice-Hall.
Ramachandran V. S. & Blakeslee S. (1998) Phantoms in the Brain: Probing the Mysteries of the Human Mind. New York: Morrow & Co.
Tse, P. U. (1998). Illusory volumes from conformation. Perception, 27(8):977–994.
Tse, P. U. (1999). Volume Completion. Cognitive Psychology, 39: 37–68.
Velmans, M. (2000) Understanding Consciousness . London: Routledge/Psychology Press.
Ware C, Kennedy J M, (1977) "Illusory line linking solid rods" Perception 6(5) 601 – 602
Wertheimer, M. (1912) Experimentelle Studien uber das Sehen von Bewegung. Zeitschrift fur Psychologie, 61, 161-265.
Yarbus A. L. (1967) Eye Movements and Vision. New York: Plenum Press.