| Previous | Return to Steve Lehar | Next |
Consider the evidence of phenomenal perspective. Mathematically, perspective is defined as a transformation from a three-dimensional world, through a focal point, onto a two-dimensional projection. However phenomenal perspective does not appear as a two-dimensional projection, but as a distortion applied to a solid volumetric space. When standing on a long straight road, the sides of the road are perceived to meet at a point up ahead, and if you turn around, they converge also to a point back behind. And yet the sides of the road also appear to be straight and parallel throughout their entire length.
Nowhere in the objective world of external reality is there anything remotely resembling perspective as we observe it in phenomenal experience. The prominant violation of Euclidean geometry in phenomenal perspective is perhaps the clearest evidence for the world of experience as an internal rather than an external entity, for the curvature of perceived space is clearly not a property of the world itself, only of our perceptual representation of it.
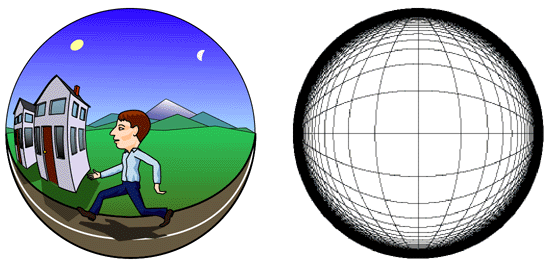
What does it mean for a space to be curved? If it is the space itself which is curved, rather than just the objects within that space, then it is the definition of straightness itself which is curved in that space. In other words if the space were filled with a set of grid-lines marking straight lines with uniform spacing, those lines themselves would be curved rather than straight, as they are in Euclidean space. However the curvature would not be apparent to creatures who live in that curved space, because the curves that are followed by those grid lines are the very definition of straightess in that space. In other words a curved object in that curved space would be defined as perfectly straight, as long as the curvature of the object exactly matched the curvature of the space it was in. If you are having difficulty picturing this paradoxical concept, and suspect that it embodies a contradiction in terms, just look at phenomenal perspective which has exactly that paradoxical property. For phenomenal perspective embodies exactly that same contradiction in terms, with parallel lines meeting at two points while passing to either side of the percipient, and while being perceived to be straight and parallel and equidistant throughout their length. This absurd contradiction is clearly not a property of the physical world, which is measurably Euclidean at least at the familiar scale of our everyday environment. Therefore that curvature must be a property of perceived space, thereby confirming that perceived space is not the same as the external space of which it is an imperfect replica.
In fact, the observed warping of perceived space is exactly the property that allows the finite representational space to encode an infinite external space. This property is achieved by using a variable representational scale, i.e. the ratio of the physical distance in the perceptual representation relative to the distance in external space that it represents. This scale is observed to vary as a function of distance from the center of our perceived world, such that objects close to the body are encoded at a larger representational scale than objects in the distance, and beyond a certain limiting distance the representational scale, at least in the depth dimension, falls to zero, i.e. objects beyond a certain distance lose all perceptual depth. This is seen for example where the sun and moon and distant mountains appear as if cut out of paper and pasted against the dome of the sky.
Psychophysical evidence for the curvature of perceived space can be found in the Hallway Experiment.
See also the distinction between objective v.s. projective instructions in psychophysical studies of perceived size.
| Previous | Return to Steve Lehar | Next |