
See also Part II of this paper: Computational Implications of Gestalt Theory II
There are several aspects of perceptual processing that were identified by Gestalt theory which remain as mysterious today computationally as they were when originally identified decades ago. These phenomena include emergence, reification or filling-in, and amodal perception. Much of the difficulty in characterizing these aspects of perceptual phenomena stems from the contemporary practice of modeling perceptual phenomena in neural network terms, even though the mapping between perception and neurophysiology remains to be identified. In fact, the reason why those particular aspects of perception have received less attention is exactly because they are particularly difficult to express in neural network terms. An alternative perceptual modeling approach is proposed, in which computational models are designed to model the percept as it is experienced subjectively, as opposed to the neurophysiological mechanism by which that percept is supposedly subserved. This allows the modeling to be conducted independent of any assumptions about the neurophysiological mechanism of vision. Illusory phenomena such as the Kanizsa figure can thereby be modeled as a computational transformation from the information present in the visual stimulus, to the information apparent in the subjective percept. This approach suggests a multi-level processing model with reciprocal feedback, to account for the observed properties of Gestalt illusions. In the second paper of this series the modeling is extended to focus on more subtle second order phenomena of illusory contour completion.
Gestalt theory represents a paradigm shift in our concepts of visual computation. The nature of the perceptual phenomena identified by Gestalt theory challenged the most fundamental notions of perceptual processing of its day, and continues to this day to challenge the notion that global aspects of perception are assembled from locally detected features. Despite these advances of Gestalt theory, the notion of visual processing as a feed- forward progression through a hierarchy of feature detectors remains the dominant paradigm of visual computation. This can be attributed in large part to neurophysiological studies which have identified single cells that appear to behave as feature detectors, tuned to simpler features in subcortical and primary cortical areas, and to more complex features in higher cortical areas in an apparently hierarchical progression. The problem with this notion of visual processing was demonstrated decades ago by Gestalt theory. For example Figure 1 a shows the camouflage triangle (camo-triangle) whose sides are defined by a large number of apparently chance alignments of visual edges. What is remarkable about this percept is that the triangle is perceived so vividly despite the fact that much of its perimeter is missing. Furthermore, visual edges which form a part of the perimeter are locally indistinguishable from other less significant edges. Therefore any local portion of this image does not contain the information necessary to distinguish significant from insignificant edges. This figure therefore reveals a different kind of processing in which global features are detected as a whole, rather than as an assembly of local parts. Although Gestalt theory identified this holistic, or global-first processing as a significant factor in human perception, the computational principles behind this kind of processing remain obscure.

This paper is the first in a two-part series whose general goal is the identification of the computational principles which underlie the kind of global processing identified by Gestalt theory, and to replicate the kind of emergence observed in perceptual phenomena using computer simulations. In this first paper of the series the focus is on the computational principles behind emergence in perception, and the generative or constructive aspect of perception identified by Gestalt theory. This analysis will suggest a functional role for feedback pathways in the visual system, and show how a hierarchical architecture need not imply a feed-forward progression from lower to higher levels of visual representation. In the second paper of the series (Lehar 1999 b) the analysis will be extended to a quantitative characterization of the process of illusory contour formation, and what it reveals about the nature of the visual mechanism. Contrary to contemporary practice, the modeling presented in these first two papers is not expressed in terms of neural networks, or a model of neurophysiology, but rather as perceptual models that replicate the observed properties of perception independent of the neural mechanism by which that perception is subserved. This approach permits the use of computational algorithms which might be considered neurophysiologically implausible. However I will show that these apparently implausible computations successfully replicate the observed properties of perception using computational principles like spatial diffusion and relaxation to dynamic equilibrium, as suggested by Gestalt theory. This in turn casts doubt on our most fundamental concepts of neural processing.
Gestalt theory suggests that visual processing occurs by a process of emergence, a dynamic relaxation of multiple constraints simultaneously, so that the final percept represents a stable state, or energy minimum of the dynamic system. Koffka (1935) exemplified this concept with the analogy of the soap bubble, whose global shape emerges under the simultaneous action of innumerable local forces. The final spherical shape is therefore determined not by a rigid template of that shape, but by a lowest-energy configuration of the system as a whole. This system of forces therefore encodes not only a single shape, but a family of shapes, for example bubbles of different sizes, as well as the infinite variety of transient shapes observed while a bubble is being inflated on a wire hoop, all with a single mechanism. Furthermore, the spherical shape defined by these forces is not rigid like a template, but elastic, like a rubber template that is free to deform as necessary in response to ambient conditions. A key characteristic of this kind of emergent process is the principle of reciprocal action between the elements of the system. For example if a portion of the bubble pushes on a neighboring portion in a certain direction, that neighbor will either succumb to the force with little resistance, or if it is constrained by opposing forces, for example by the wire hoop on which the bubble is anchored, that resistance is communicated back reciprocally to the original element, pushing on it in the opposite direction. The principal thesis of the present paper is that this law of reciprocal action represents the guiding principle behind feedback in visual processing. For example in the case of the camo triangle, this principle is observed along the contour of the illusory triangle, where local edge signals appear to reinforce one another wherever they are aligned in a globally consistent collinear configuration, resulting in the emergence of a global perceived contours. On the other hand local edges that fail to find global support will be suppressed by the conflicting forces exerted by neighboring edge fragments. The same principle is active between different representational levels in the visual hierarchy. I propose therefore a Multi-Level Reciprocal Feedback model (MLRF) of visual processing to explain the role of feedback connections as communicating constraints experienced in higher representational levels back to lower levels where those constraints are expressed in a form appropriate to those lower levels. Therefore the entire visual hierarchy defines a coupled dynamic system whose equilibrium state represents a balance or dynamic compromise between constraints experienced at all levels simultaneously, as suggested by Gestalt theory.
Visual illusions offer a convenient starting point for investigating the mechanism of perception, for a feature that is seen subjectively in the absence of a corresponding feature in the stimulus provides direct evidence of the interactions underlying perception. Consider the Kanizsa figure, shown in Figure 1 b. In this figure, an illusory contour is observed to form between pairs of edges in the stimulus that are aligned in a collinear configuration. A number of neural network models have been proposed to account for collinear completion of the sort observed in the Kanizsa figure (Grossberg & Mingolla 1985, Walters (1986). There is however a problem inherent in modeling visual illusions by neural network models. A visual illusion is a subjective perceptual phenomenon, whose properties can be measured using psychophysical experiments. A neural network model on the other hand models the neurophysiological mechanism of vision, rather than the subjective experience of visual perception. Until a mapping is established between subjective experience and the corresponding neurophysiological state, there is no way to verify whether the neural model has correctly replicated the illusory effect. The Kanizsa figure exemplifies this problem. The subjective experience of this illusion consists not only of the emergent collinear boundary, but the illusory triangle is perceived to be filled in perceptually with a uniform surface brightness that is perceived to be brighter than the white background of the figure. The subjective experience of the Kanizsa figure therefore can be depicted schematically as in Figure 1 c. Furthermore, the three pac-man features at the corners of the triangle are perceived as complete circles occluded by the foreground triangle, as suggested in Figure 1 d. There is considerable debate as to how this rich spatial percept is encoded neurophysiologically, and it has even been suggested (Dennett 1991, 1992, O'Regan 1992) that much of this perceptual information is encoded only implicitly, i.e. that the subjective percept is richer in information than the neurophysiological state that gives rise to that percept. This view however is inconsistent with the psychophysical postulate (Müller 1896, Boring 1933) which holds that every aspect of the subjective experience must have some neurophysiological counterpart.
One way to circumvent this thorny issue is by performing perceptual modeling as opposed to neural modeling, i.e. to model the information apparent in the subjective percept rather than the objective state of the physical mechanism of perception. In the case of the Kanizsa figure, for example, the objective of the perceptual model, given an input of the Kanizsa figure, is to generate a perceptual output image similar to Figure 1 c that expresses explicitly the properties observed subjectively in the percept. Whatever the neurophysiological mechanism that corresponds to this subjective experience, the information encoded in that physiological state must be equivalent to the information apparent in the subjective percept. Unlike a neural network model, the output of a perceptual model can be matched directly to psychophysical data, as well as to the subjective experience of perception.
The perceptual modeling approach immediately reveals that the subjective percept contains more explicit spatial information than the visual stimulus on which it is based. In the Kanizsa triangle in Figure 1 b the triangular configuration is not only recognized as being present in the image, but that triangle is filled-in perceptually, producing visual edges in places where no edges are present in the input. Furthermore, the illusory triangle is filled-in with a white that is brighter than the white background of the figure. Finally, the figure produces a perceptual segmentation in depth, the three pac-man features appearing as complete circles, completing amodally behind an occluding white triangle. This figure demonstrates that the visual system performs a perceptual reification, i.e. a filling-in of a more complete and explicit perceptual entity based on a less complete visual input. The identification of this generative or constructive aspect of perception was one of the most significant achievements of Gestalt theory, and the implications of this concept have yet to be incorporated into computational models of perception.
The subjective percept of the Kanizsa figure contains more information than can be encoded in a single spatial image. For although the image of the explicit Kanizsa percept in Figure 1 c expresses the experience of the Kanizsa figure of Figure 1 b, a similar figure cannot be devised to express the experience of the camo-triangle in Figure 1 a, where the perceived contours carry no brightness information as do those in the Kanizsa figure. The perceptual reality of this invisible structure is suggested by the fact that this linear percept can be localized to the highest precision along its entire length, it is perceived to exist simultaneously along its entire length, and its spatial configuration is perceived to be the same across individuals independent of their past visual experience. Michotte (1964) refers to such percepts as amodal in the sense that they are not associated with any perceptual modality such as color, brightness, or stereo disparity, being seen only as an abstract grouping percept. And yet the amodal contour is perceived as a vivid spatial entity, and therefore a complete perceptual model would have to register the presence of such vivid amodal percepts with an explicit spatial representation. In a perceptual model this issue can be addressed by providing two distinct representational layers, one for the modal, and the other for the amodal component of the percept, as seen in Grossberg's Boundary Contour System / Feature Contour System (BCS / FCS) (Grossberg & Mingolla 1985, Grossberg & Todorovic 1988), where the FCS image represents the modal brightness percept, whereas the BCS image represents the amodal contour percept. The amodal contour image therefore represents the information captured by an outline sketch of a scene, which depicts edges of either contrast polarity as a linear contour in a contrast-independent representation. A full perceptual model of the experience of the Kanizsa figure therefore could be expressed by the two images of Figure 1 c and d, to express the modal and amodal components of the percept respectively. While the edges present in Figure 1 d are depicted as dark lines, these lines by definition represent invisible or amodal linear contours in the Kanizsa percept. Note that in this example the illusory sides of the Kanizsa figure register in both modal and amodal percepts, but the hidden portions of the black circles are perceived to complete amodally behind the occluding triangle in the absence of a corresponding perceived brightness contour. This kind of double representation can now express the experience of the camo triangle, whose modal component would correspond exactly to Figure 1 a, without any explicit brightness contour around the triangular figure, and an amodal component that would consist of a complete triangular outline, together with the multiple outlines of the visible fragments in the image.
There are several visual phenomena which suggest an intimate coupling between the modal and amodal components of the percept. Figure 2 a depicts three dots in a triangular configuration that generates an amodal triangular contour connecting the three dots. This grouping percept is entirely amodal, and it might be argued that there is no triangle present in this percept. And yet the figure is naturally described as a "triangle of dots", and the invisible connecting lines are localizable to the highest precision. Furthermore, the amodal triangle can be transformed into a modal percept, and thus rendered visible, as shown in Figure 2 b, where the three "v" features render the amodal grouping as a modal surface brightness percept. Figure 2 c demonstrates another transformation from an amodal to a modal percept. The boundary between the upper and middle segments of Figure 2 c are seen as an amodal grouping contour, devoid of any brightness component. When however the line spacing on either side of this contour is unequal, as in the boundary between the middle and lower portions of this figure, then the amodal contour becomes a modal one, separating regions of slightly different perceived brightness. Figure 2 d shows how the camo triangle can also be transformed into a modal percept by arranging for a different density of texture elements in the figure relative to the ground, producing a slight difference in surface brightness between figure and ground. These properties suggest that modal and amodal contours are different manifestations of the same underlying mechanism, the only difference between them being that the modal contours are made visible by features that provide a contrast difference across the contour.
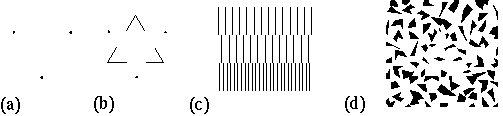
As the phenomena addressed by models of perception become increasingly complex, so too must the models designed to account for those phenomena, to the point that it becomes difficult to predict the response of a model to a stimulus without extensive computer simulations. In contrast to the neural network approach, the focus here will be on perceptual modeling, i.e. on the kinds of computation required to reproduce the observed properties of illusory figures without regard to issues of neural plausibility. In other words, the focus will be on the information processing manifest in perceptual phenomena, rather than on the neurophysiological mechanism of the visual system. Since illusory phenomena reveal spatial interactions between visual elements, perceptual processing will be expressed in terms of the equivalent image processing operations required to transform an input like the Kanizsa figure of Figure 1 b to explicit modal and amodal representations of the subjective experience of perception.
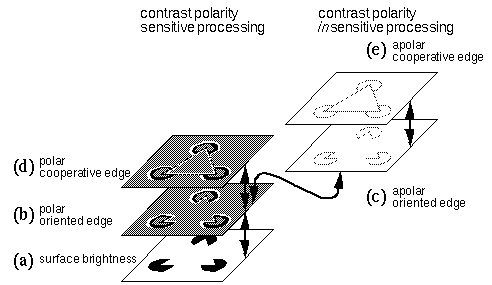
Figure 3 summarizes the computational architecture of the MLRF model. Figure 3 a depicts the surface brightness layer. Initially, this layer represents the pattern of luminance present in the visual stimulus. A process of image convolution transforms this surface representation into an edge representation that encodes only the brightness transitions at visual edges, but preserves the contrast polarity across those edges, resulting in a contrast-polarity-sensitive, or polar edge representation shown in figure 3 b. This operation represents a stage of abstraction, or reduction of image information to essential features. A further level of abstraction then drops the information of contrast polarity, resulting in a contrast-polarity-insensitive representation, or apolar edge layer, shown in figure 3 c. Next, a cooperative processing stage operates on both the polar and apolar edge images to produce polar and apolar cooperative edge layers, shown in Figure 3 d and e respectively. The feed-forward processing summarized so far is consistent with the conventional view of visual processing in terms of a hierarchy of feature detectors at different levels. I will then show how a reverse-transformation can be defined to reverse the flow of data in a top-down direction, by the principle of reciprocal action, and this processing performs a reification, or reconstructive filling-in of the information present in the higher levels of the hierarchy. In the case of the Kanizsa stimulus, the effect of this top-down reification is to express back at the surface brightness level, those features that were detected at the higher levels of the hierarchy, such as the collinear alignment between the inducing edges. This reification explains the appearance of the illusory triangle as a surface brightness percept.
While image processing is defined in terms of quantized digital images and sequential processing stages, the model developed below is intended as a digital approximation to a parallel analog perceptual mechanism that is continuous in both space and time, as suggested by Gestalt theory. The field-like interactions between visual elements will be modeled with image convolution operations, where the convolution kernel represents a local field-like influence at every point in the image. The principle of emergence in perception will be modeled by an iterative algorithm that repeats the same sequence of processing stages until equilibrium is achieved. While the computer algorithm is only an approximation to the continuous system, the quantization in space and time, as well as the breakdown of a complex parallel process into discrete sequential stages, offers also a clear way of describing the component elements of a computational mechanism that operates as a continuous integrated whole.
In theoretical terms, the images generated in the following simulations can be considered as arrays of fuzzy logic units whose analog values represent a measure of confidence for the presence of particular features at a particular location in the visual field. For this reason, pixel values in these simulations are bounded in the range 0 to 1, or where appropriate, -1 to +1, where +1 represents maximal confidence for the presence of some feature, and -1 represents maximal confidence for the presence of a complimentary feature, darkness v.s. brightness, dark/bright edge v.s. bright/dark edge, etc.
The next section begins with a description of common image processing operations that are used in various neural network models to account for collinear illusory contour formation, with a focus on the spatial effects of each stage of processing, and how they relate to the observed properties of the percept. Later I will show the limitations of current models of these effects, and how further application of Gestalt principles leads to a more general model with greater predictive power. For clarity and historical consistency, the neural network terminology of cells and receptive fields will be used in the following discussion where appropriate to describe computational concepts inherited from the neural network modeling approach.
In image processing, edges are detected by convolution with a spatial kernel (Ballard & Brown, 1982), that operates like a template match between the image and the kernel. In the convolution process the kernel is effectively scanned across the image in a raster pattern, and at every spatial location, a measure of match is computed between the kernel and the underlying local region of the image. The output of this convolution is an image whose pixels represent this match measure at every spatial location in the original image. A template used for edge detection has the form of a local section of an edge, i.e. the kernel has positive and negative halves, separated by an edge at some orientation, representing a light / dark edge at that orientation, like the one shown in Figure 4 b. Such an edge detector produces a strong positive response wherever the template is passed over edges of the same light / dark polarity and orientation in the image, and a strong negative response is produced over edges of that same orientation but of the opposite contrast polarity. Over uniform regions, or over edges of orientations very different from that of the template, the response to the kernel is weak or zero. The output of this processing therefore is itself an image, of the same dimensions as the original image, except that the only features present in this image are regions of positive and negative values that correspond to detected edges in the original. This operation is also known as spatial filtering, because the kernel, or spatial filter, extracts from the input only those features that match the kernel.
For consistency with the fuzzy logic concept, the magnitudes of the filter values have been scaled so as to produce an output value of +1 in response to an "ideal" feature, in the case of Figure 4 b an "ideal edge" being defined as a sharp vertical boundary between dark (value 0) and bright (value 1) patches in the input brightness image. A filter of this sort is known as a match filter, since it computes a measure of match between the image and the feature encoded in the filter. Fuzzy logic operations are defined as functions on discrete inputs, for example a fuzzy AND or fuzzy OR function operates on a discrete number of fuzzy logic variables. The image convolution on the other hand represents more of a field-like influence which, in the continuous case, operates on a field or spatial region of the input. While the output of the convolution can be considered as a point by point result, the real significance of the output is seen in the spatial pattern of values in the output field. The image convolution can therefore be seen as a fuzzy spatial logic operator, that performs spatial computations on a spatial input pattern to produce a spatial output pattern expressed as fuzzy logic fields, or probability distribution functions.
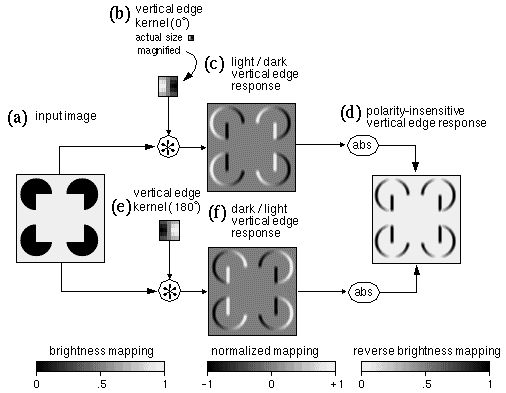
Figure 4 illustrates the process of spatial filtering by image convolution. The input image shown in Figure 4 a represents the luminance profile of a Kanizsa figure composed of bright and dark regions in the range 0 for dark, and 1 for bright. In this example the image dimensions are 88 x 88 pixels. The convolution filter shown in Figure 4 b is a vertical edge detector of light / dark contrast polarity and of orientation 0°. This particular filter is defined by the sum of two Gaussian functions, one positive and one negative, displaced in opposite directions across the edge, as defined by the equation

|
(EQ 1) |
where Fxy is the filter value at location (x,y) from the filter origin, q is the orientation of the edge measured clockwise from the vertical, and d is the displacement of each Gaussian across the edge on opposite sides of the origin. Kernels of this sort are generally balanced so that the filter values sum to zero, as is the practice in image processing to prevent the filtering process from adding a constant bias to the output image. In image processing, the spatial kernel is generally very much smaller than the image, in this case the filter used was 5 by 5 pixels. Figure 4 b shows this kernel both at actual size, i.e. depicted at the same scale as the input image, and magnified, where the quantization of the smooth Gaussian function into discrete pixels is apparent. The filter is displayed in normalized mapping, i.e. with negative values depicted in darker shades, positive values in lighter shades, and the neutral gray tone representing zero response to the filter.
The image convolution is defined by
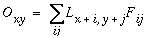
|
(EQ 2) |
where Oxy is the oriented edge response to the filter at location (x,y) in the image, (i,j) are the local displacements from that location, and Lx+i,y+j is the image luminance value at location (x+i,y+j). Figure 4 c shows the output of the convolution, again in normalized mapping. The vivid three-dimensional percept of raised surfaces observed in this image is spurious, and should be ignored. Note how the filter response is zero (neutral gray) within regions of uniform brightness in the original, both in uniform dark and bright areas. A positive response (bright contours) is observed in response to edges of the same light / dark contrast polarity as the filter, while a negative response (dark contours) occurs to edges of the opposite contrast polarity. Due to the use of match filters, the maximum and minimum values in this output image are +1 and -1 respectively, representing a fuzzy logic confidence for the presence of the feature encoded in the filter at every point in the image.
Figure 4 f shows the response to the same input by a vertical edge filter of orientation 180°, shown in Figure 4 e, and the output is the same as the response to the 0° filter except with positive and negative regions reversed.
Often, the contrast polarity of edges is not required, for example a vertical edge might be registered the same whether it is of a light/dark or dark/light contrast polarity. In such cases an apolar edge representation can be used by applying an absolute value function to either Figure 4 c or f to produce the apolar edge image shown in Figure 4 d, as defined by the equation
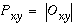
|
(EQ 3) |
For this image, a reverse-brightness mapping is used for display, i.e. the dark shades represent a strong response to vertical edges of either contrast polarity, and lighter or white shades represent weaker or zero response respectively. The reason for using the reverse mapping in this case, besides saving ink in a mostly zero-valued image, is because of nonlinearities in the printing process which make it easier to distinguish small differences in lighter tones than in darker tones. Since the focus of this paper is on illusory contours, the reverse mapping highlights these faint traces of low pixel values. Since illusory contour formation is often observed to occur even between edges of opposite contrast polarity, models of illusory contour formation often make use of this apolar oriented edge representation (Zucker et al. 1988, Hubel 1988, Grossberg & Mingolla 1985, Walters 1986).
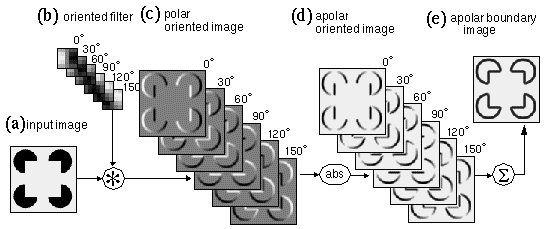
The image convolutions demonstrated in Figure 4 show only detection of vertically oriented edges. In order to detect edges of all orientations the image must be convolved with an array of spatial filters, encoding edges at a range of orientations. For example there might be twelve discrete orientations at 30 degree intervals, encoded by twelve convolution kernels. Convolving a single image with all twelve oriented kernels therefore produces a set of twelve oriented edge images, each of which has the dimensions of the original image. If the absolute value function is to be applied, only half of these convolutions need actually be performed. In much of the following discussion therefore, oriented edge filtering will be performed using six orientations at 30° intervals from 0° to 150°, representing twelve polar orientations from 0° to 330°. Figure 5 depicts a set of convolutions of the Kanizsa image with a bank of oriented edge filters, followed by an absolute value function, to produce a bank of apolar oriented edge responses. The filter and the oriented response are three-dimensional data structures, with two spatial dimensions and a third dimension of orientation. The response of cells in the primary visual cortex has been described in terms of oriented edge convolution (Hubel 1988), where the convolution operation is supposedly performed by a neural receptive field, whose spatial pattern of excitatory and inhibitory regions match the positive / negative pattern of the convolution kernel. This data structure therefore is believed to approximate the information encoded by cells in the primary visual cortex. The utility of spatial filtering with a bank of oriented filters is demonstrated by the fact that most models of illusory contour formation are based on this same essential principle. For the three-dimensional data structure produced by oriented convolution contains the information required to establish collinearity in an easily calculable form, and therefore this data structure offers an excellent starting point for modeling the properties of the illusory contour formation process, both for neural network and for perceptual models. For convenience, the entire three-dimensional structure will be referred to as the oriented image, which is composed of discrete orientation planes, (henceforth contracted to oriplanes) one for each orientation of the spatial filter used. Figure 5 e shows a sum of all of the oriplanes in the apolar edge image of Figure 5 d, to show the information encoded in that data structure in a more intuitively meaningful form. In this oriplane summation, and in others shown later in the paper, a nonlinear saturation function of the form f(x) = x/(a+x) is applied to the summed image in order to squash the image values back down to the range 0 to 1 in the apolar layers, or from -1 to +1 in the polar cases, while preserving the low values that might be present in individual oriplanes.
Examination of the curved portions of the pac-man figures in the oriented image in Figure 5 d reveals a certain redundancy, or overlap between oriplanes. This effect is emphasized in Figure 6 a, which shows just the upper- left pac-man figure for the first four oriplanes. Ideally, the vertical response should be strong only at the vertical portions of the curve, and fall off abruptly where the arc curves beyond 15 degrees, where the response of the 30 degree filter should begin to take over. Instead, we see a significant response in the vertical oriplane through about 60 degrees of the arc in either direction, and in fact, the vertical response only shows significant attenuation as the edge approaches 90 degrees in orientation. This represents a redundancy in the oriented representation or a duplication of identical information across the oriplanes. The cause of this spread of signal in the orientation dimension is limited sharpness in orientational tuning of the filter. One way to sharpen the orientational tuning is by elongating the oriented filter parallel to the edge in the kernel so as to sample a longer portion of the edge in the image. But this enhanced orientational tuning comes at the expense of spatial tuning, since such an elongated edge detector will produce an elongated response beyond the end of every edge in the image, i.e. there is a trade- off between spatial v.s. orientational tuning where an increase in one is balanced by a reduction in the other. The segregation of orientations in the oriented image offers an alternative means of sharpening the orientational tuning without compromising the spatial tuning. This is achieved by establishing a competition between oriplanes at every spatial location. The competition should not be absolute however, for example by preserving only the maximal response at any spatial location, because there are places in the image that legitimately represent multiple orientations through that point, for example at the corner of the square, where both horizontal and vertical edge responses should be allowed. A softer competition is expressed by the equation
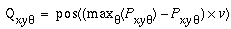
|
(EQ 4) |

where Q represents the new value of the oriented image after the competition, the function pos() returns only the positive portion of its argument and zero otherwise, the function maxq() returns the maximum oriented response at location (x,y) across all orientations q, and the value v is a scaling factor that adjusts the stiffness of the competition. This equation is a static approximation to a more dynamic competition or lateral inhibition across different oriplanes at every spatial location, as suggested by Grossberg & Mingolla (1985). Figure 6 b shows the effects of this competition in reverse-brightness mapping mode, where the response of the vertical oriplane is now observed to fall off approximately where the 30 degree oriplane response picks up, so that the oriented information is now better partitioned between the different oriplanes. Figure 7 a shows the effect of oriented competition on the whole image. A similar oriented competition can be applied to the polar representation, producing the result shown in Figure 8 a.
The formation of illusory contours by collinearity, as exemplified in the Kanizsa figure, is observed to occur between edges that are 1: parallel, and 2: spatially aligned in the same direction as their common orientation, as long as 3: their spatial separation in that direction is not too great. The oriented image described above offers a representation in which collinearity can be easily calculated, for each oriplane of that structure is an image that represents exclusively edges of a particular orientation. Therefore all edge signals or active elements represented within a single oriplane fulfill the first requirement of collinearity, i.e. of being parallel to each other in orientation. The second and third requirements, being spatially aligned and nearby in the oriented direction, can also be readily calculated from this image by identifying regions of high value within an oriplane that are separated by a short distance in the direction of the corresponding orientation. For example in the vertical oriplane, a vertical illusory contour is likely to form between regions of high value that are related by a short vertical separation.
Collinearity in the oriented image can therefore be computed with another image convolution, this time using an elongated spatial kernel which Grossberg calls the cooperative filter, whose direction of elongation is matched to the orientation of the oriplane in question. An elongated kernel of this sort produces a maximal response when located on elongated features of the oriented image, which in turn correspond to extended edges in the input. It will also however produce a somewhat weaker response when straddling a gap in a broken or occluded edge in the oriented image. This filtering will therefore tend to link collinear edge fragments with a weaker boundary percept in the manner observed in the Kanizsa illusion and the camo triangle. If the magnitude of the filter value is made to decrease smoothly with distance from the center of the filter, this convolution will produce illusory contours whose strength is a function of the proximity between oriented edges, as is observed in the Kanizsa figure. The output of this stage of processing is called the cooperative image, and it has the same dimensions as the oriented image.
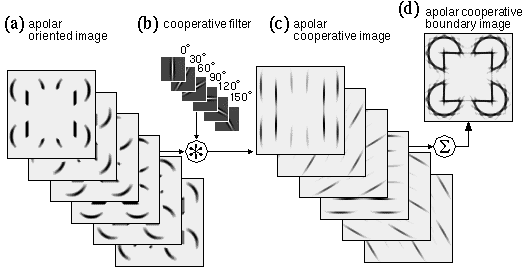
Figure 7 illustrates cooperative processing of the oriented image, shown in Figure 7 a, using a cooperative convolution filter defined by
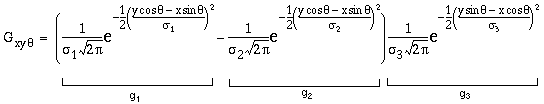
|
(EQ 5) |
This is a Gaussian function (g3) in the oriented direction (e.g. in the vertical direction for the vertical oriplane) modulated by a difference-of-Gaussians function (g1 - g2) in the orthogonal direction (e.g. in the horizontal direction for the vertical oriplane). Figure 7 b shows the shape of this convolution filter depicted in normalized mapping, i.e. with positive values depicted in lighter shades, and negative values in darker shades, with a neutral gray depicting zero values. A Gaussian profile in a spatial filter performs a blurring function, i.e. it spreads every point of the input image into a Gaussian function in the output. A difference-of-Gaussians on the other hand represents a sharpening, or deblurring filter as used in image processing, i.e. one that tends to invert a blur in the input, or amplify the difference between a pixel and its immediate neighbors. In this case, the cooperative filter performs a blurring in the oriented direction, and an image de-blurring or sharpening in the orthogonal direction. In these simulations the ratio s2 = 1.6 s1 was used for the difference-of-Gaussians as suggested by Marr (1982 p 63). The convolution is described by
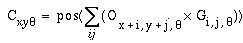
|
(EQ 6) |
where Cxyq is the response of the cooperative filter at image location (x,y) and orientation q. Note that in this convolution each oriplane of the oriented image is convolved with the corresponding oriplane of the cooperative filter to produce an oriplane of the cooperative image. The effect of this processing is to smear or blur the pattern from the oriented image in the oriented direction. For example the vertical oriplane of the oriented image, shown in Figure 7 a is convolved with the vertical plane of the cooperative filter, shown in Figure 7 b, to produce the vertical plane of the cooperative image, as shown in Figure 7 c. Notice how the lines of activation in the cooperative image are somewhat thinner than the corresponding lines in the oriented image, due to the sharpening effect of the negative side-lobes in the filter. This feature therefore serves to improve the spatial tuning of the oriented filtering of the previous processing stage, to produce the sharp clear contours observed in the Kanizsa illusion.
If cooperative filtering is to be performed in a single pass, the length of the cooperative filter must be sufficient to span the largest gap across which completion is to occur, in this case the distance between the pac-man inducers. The cooperative filter shown in Figure 7 b therefore is very much larger (35 x 35 pixels) than the oriented filter shown in Figure 5 b which was only 5 x 5 pixels, and in fact, Figure 7 b depicts the cooperative filter at the same scale as the input image, rather than magnified.The effect of this cooperative processing is shown in Figure 7 c, where every point of the oriented image is spread in the pattern of the cooperative filter. Note particularly the appearance of a faint vertical linking line between the vertical edges in the vertical cooperative oriplane, which demonstrates the most essential property of cooperative processing. Figure 7 d reveals the effects of this cooperative processing in more meaningful terms by summing the activation in all of the oriplanes of the cooperative image in Figure 7 c, showing the complete illusory square.
The boundary processing described above represents the amodal component of the percept, i.e. Figure 7 d should be compared with Figure 1 d. In terms of fuzzy logic the response of a cooperative unit represents the confidence for the presence of an extended visual edge at a particular location and orientation in the visual field. The vertical blurring of this signal in the cooperative layer can be seen as a field-like hypothesis building mechanism based on the statistical fact that the presence of an oriented edge at some location in the image is predictive of the presence of further parts of that same edge at the same orientation and displaced in the collinear direction, and the certainty of this spatial prediction decays with distance from the nearest detected edges. The cooperative processing of the whole image shown in Figure 7 d can therefore be viewed as a computation of the combined probability of all hypothesized edges based on actual edges detected in the image. That probability field is strongest where multiple edge hypotheses are superimposed, representing a cumulative or conjoint probability of the presence of edges inferred from those detected in the input.
While this processing does indeed perform the illusory completion, there are a number of additional artifacts observed in Figure 7 d. In the first place, the edges of the illusory square overshoot beyond the corners of the square. This effect is a consequence of the collinear nature of the processing, which is by its nature unsuited to representing corners, vertices, or abrupt line-endings, and a similar collinear overshoot is observed where the circumference of the pac-man feature intersects the side of the illusory square. Another prominent artifact is a star-shaped pattern around the curved perimeter of the pac-man features. This is due to the quantization of orientations in this example into 12 discrete directions (6 orientations), each oriplane of the cooperative filter attempting to extend a piece of the arc along a tangent to the arc at that orientation. These artifacts will be addressed in detail in a companion paper (Lehar 1999 b) where the model will be refined to eliminate those undesirable features. With these reservations in mind, Figure 7 d demonstrates the principle of calculating a collinear illusory contour by convolution of the oriented image with an elongated cooperative filter. The computational mechanism of cooperative filtering of an oriented image representation therefore replicates some of the perceptual properties of illusory contour formation. Several models of illusory contours or illusory grouping percepts (Grossberg & Mingolla 1985, Walters 1986, Zucker et al. 1988, Parent & Zucker 1989) operate on this basic principle, although there is considerable variation in the details.
The cooperative filtering described above is applied to the apolar oriented edge representation in order to allow collinear completion to occur between edges of opposite direction of contrast, as is observed in the camo-triangle of Figure 1 a. However in the case of the Kanizsa figure, the surface brightness percept preserves the direction of contrast of the inducing edges, which suggests that the edge signal that propagates between the inducers can carry contrast information when it is available, or when it is consistent along an edge, although the amodal completion survives independently even along edges of alternating contrast polarity, as observed in the camo triangle. In terms of fuzzy logic, an edge of one contrast polarity is predictive of adjacent collinear edge signals of the same contrast polarity, unless contrast reversals are detected along the same edge. Polar collinear boundary completion can be computed very easily from the polar oriented edge representation depicted in Figure 5 c by performing cooperative filtering exclusively on the positive values of the polar oriented edge image, producing a polar cooperative response from 0° through 150°, and then again exclusively on the negative values of the polar image producing the polar cooperative response from 180° through 330°. In other words, the polar cooperative image must have twice as many oriplanes as the apolar representation to accommodate the two directions of contrast for each orientation. Alternatively, as with the polar oriented representation itself, the polar cooperative image can be encoded in both positive and negative values, the former representing collinear edges of one contrast polarity, while the latter represents the opposite contrast polarity, with both positive and negative values expressed in a single image. This compression is valid because the two contrast polarities are mutually exclusive for any particular location on an edge.
Figure 8 demonstrates polar collinear boundary completion by convolution of the polar oriented edge image in Figure 8 a with the cooperative filter shown in Figure 8 b. Figure 8 c shows the polar cooperative response, where the positive (light shaded) regions denote cooperative edges of dark/light polarity, and the negative (dark shaded) regions of Figure 8 c denote cooperative edges of light/dark polarity, using the same polarity encoding as seen in Figure 8 a. Figure 8 d shows the sum of the oriplanes in Figure 8 c to demonstrate intuitively the nature of the information encoded in the oriplanes of Figure 8 c. Note the emerging illusory contours in this figure, with a dark-shaded i.e. negative contrast edge on the left side of the square, and a light-shaded positive contrast edge on the right side of the square reflecting the opposite contrast polarities.

The evidence of the Kanizsa figure reveals a kind of processing that is the inverse of abstraction, or reification, a filling-in of a more complete and explicit percept from a more compressed or abstracted stimulus. Indeed information theory suggests that a compressed representation is meaningless without a decompression algorithm capable of restoring the original uncompressed data. The illusory percept observed in the Kanizsa figure can therefore be seen as a perceptual reification of some higher level representation of the occluding figure as a whole, showing that perception occurs not by abstraction alone, but by a simultaneous abstraction and reification. The question is how the feed-forward spatial processing stream can be reversed in a meaningful manner to perform the spatial reification evident in perception. Lehar & Worth (1991) propose that this top-down feedback be computed by a reverse convolution, which is a literal reversal of the flow of data through the convolution filter as suggested by the principle of reciprocal action. In the forward convolution of oriented filtering defined in Equation 2, the single output value of the oriented edge pixel Oxy is calculated as the sum of a region of pixels in the input luminance image Lx+i,y+j, each multiplied by the corresponding filter value Fij, as suggested schematically in Figure 9 a. In the reverse convolution a region of the reified oriented image Rx+i,y+j, is calculated from a single oriented edge response Oxy which is passed backwards through the oriented filter Fij as defined by the equation
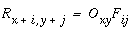
|
(EQ 7) |

This equation defines the effect of a single oriented edge response on a region of the reified image, which is to generate a complete "footprint" in the reified image in the shape of the original oriented filter used in the forward convolution as suggested schematically in Figure 9 b. The contrast of the footprint is scaled by the magnitude of the oriented response at that point, and if the oriented response is negative, then the footprint is negative also, i.e. a negative light/dark edge filter is printed top-down as a reverse contrast dark/light footprint. Any single point Rxy in the reified image receives input from a number of neighboring oriented cells whose projective fields overlap on to that point, as suggested schematically in Figure 9 c. The reified oriented image therefore is calculated as
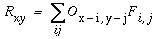
|
(EQ 8) |
or equivalently,
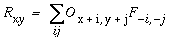
|
(EQ 9) |
It turns out therefore that the reverse convolution is mathematically equivalent to a forward convolution performed through a filter that is a mirror image of the original forward filter, reflected in both x and y dimensions, i.e. F'ij = F-i,-j. In fuzzy logic terms the reverse convolution expresses the spatial inference that the presence of an edge response at some point in the oriented image infers a corresponding spatial pattern of brightness at the image level, as defined in the oriented filter.
Figure 10 demonstrates a reverse-convolution of the polar oriented edge image, shown in Figure 10 d, back through the same oriented filter, shown in Figure 10 c by which it was originally generated, to produce the reified polar edge image, whose individual oriplanes are shown in Figure 10 b. Note how lines of positive value (light shades) in Figure 10 d become light/dark edges in Figure 10 b, while lines of negative values (dark shades) in Figure 10 d become edges of dark/light polarity in Figure 10 b. Since in the forward convolution one image was expanded into six orientation planes, in the reverse convolution the six planes are collapsed back into a single two-dimensional image by summation, as shown in Figure 10 a. Note that the reverse convolution is not the inverse of the forward convolution in the strict mathematical sense, since the reified oriented image is still an edge image rather than a surface brightness representation. This image does however represent the information that was extracted or filtered from the original image by the process of oriented filtering, but that information is now translated back to terms of surface brightness rather than of orientation, i.e. the regions of positive (light) and negative (dark) values in Figure 10 a represent actual light and dark brightness in the original image. The reason why this reified image registers only relative contrast across boundaries in the original, rather than absolute brightness values within uniform regions, is exactly because the process of oriented filtering discards absolute value information, and registers only contrast across boundaries. The reified oriented image is very similar in appearance to the image produced by convolving the original with a circular-symmetric difference-of- Gaussians filter, or equivalently, a band-pass Fourier filtering of the original. The two-dimensional polar image shown in Figure 10 a will be referred to as the polar boundary image.
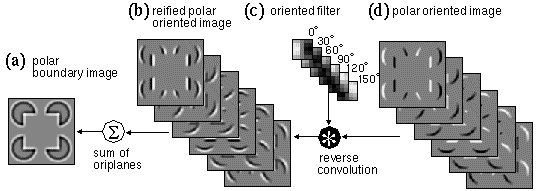
Grossberg &Todorovic (1988) suggest that the surface brightness information that is lost in the process of image convolution can be recovered by a diffusion algorithm that operates by allowing the brightness and darkness signals in the polar boundary image of Figure 10 a to diffuse outward spatially from the boundaries, in order to fill in the regions bounded by those edges with a percept of uniform surface brightness. For example the darkness signal seen along the inner perimeter of each of the four pac-man features in Figure 10 a should be free to diffuse spatially within the perimeter of those features, to produce a percept of uniform darkness within those features, as shown in Figure 11 c, while the brightness signal at the outer perimeter should be free to diffuse outwards, to produce a percept of uniform brightness between the pac-man features, as shown also in Figure 11 c. The diffusing brightness and darkness signals however are not free to diffuse across the boundaries in the image, as defined for example by the apolar boundary image shown in Figure 11 b, which was computed as the sum of oriplanes of the apolar oriented edge image, as shown also in Figure 5 e. In other words the spatial diffusion of the brightness and darkness signals is bounded or confined by the apolar boundary signal, which segments the image into disconnected regions, within each of which the perceived brightness will tend to become uniform by diffusion, just as water within a confined vessel tends to seek its own level. In fuzzy logic terms the brightness diffusion process expresses a spatial inference of the likely form of the brightness image based on the patterns of activation found in the polar and apolar boundary images.
The equation for this diffusion is derived from Grossberg's FCS model (Grossberg & Todorovic 1988), again simplified somewhat as a consequence of being a perceptual model rather than a neural model, and thereby being liberated from the constraints of "neural plausibility". The diffusion is given by
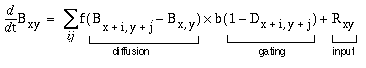
|
(EQ 10) |
where Bxy is the perceived brightness at location (x,y), which is driven by the diffusion from neighboring brightness values within the immediate local neighborhood (i,j), which in turn is proportional to the total difference in brightness level between the pixel and each of its local neighbors. A brightness pixel surrounded by higher valued neighbors will therefore grow in brightness, while one surrounded by lower valued neighbors will decline in brightness. This diffusion however is gated by the gating term, which is a function of the strength of the boundary signal Dxy at location (x,y), i.e. the gating term goes to zero as the boundary strength approaches its maximal value of +1, which in turn blocks diffusion across that point. The diffusion and the gating terms are further modulated by the diffusion or flow constant f, and the gating or blocking constant b respectively. Finally, the flow is also a function of the input brightness signal Rxy from the reified oriented image at location (x,y), which represents the original source of the diffusing brightness signal, and can be positive or negative to represent bright or dark values respectively. The computer simulations, which are otherwise intolerably slow, can be greatly accelerated by solving at equilibrium, i.e. in each iteration, each pixel takes on the average value of its eight immediate neighbors, weighted by the boundary strength at each neighboring pixel, so that neighboring pixels located on a strong boundary contribute little or nothing to the weighted average. This is expressed by the equilibrium diffusion equation
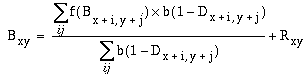
|
(EQ 11) |
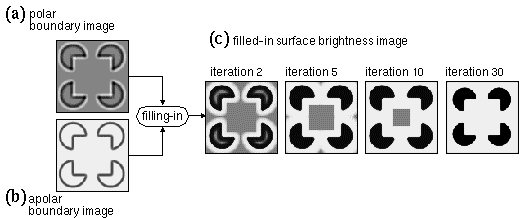
where Bxy on the left side of the equation represents the new value calculated from the previous brightness value Bxy on the right side of the equation. Figure 11 c shows the process of diffusion after 2, 5, 10, and 30 iterations of the diffusion simulation, showing how the diffusing brightness signal tends to flood enclosed boundaries with a uniform brightness or darkness percept.
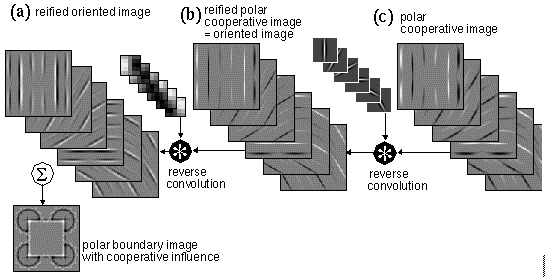
The example of forward and reverse processing represented in Figures 5, 10 and 11 is not a very interesting case, since the reified brightness percept of Figure 11 c is essentially identical in form to the input image in Figures 5 a, showing just the input stimulus devoid of any illusory components. However even in its present form the model explains some aspects of brightness perception, in particular the phenomena of brightness constancy (Spillmann & Werner 1990 p. 131) and the simultaneous contrast illusion (Spillmann & Werner 1990 p. 131), as well as the Craik-O'Brien-Cornsweet illusion (Spillmann & Werner 1990 p. 136). Brightness constancy is explained by the fact that the surface brightness percept is reified from the relative brightness across image edges, and therefore the reified brightness percept ignores any brightness component that is uniform across the edges. The effect is a tendency to "discount the illuminant", i.e. to register the intrinsic surface reflectance of an object independent of the strength of illumination. Figure 12 demonstrates this effect using exactly the same forward and reverse processing described above, this time applied to a Kanizsa figure shown in Figure 12 a to which an artificial illuminant has been added in the form of a Gaussian illumination profile that is combined multiplicatively with the original Kanizsa stimulus, as if viewed under a non-uniform illumination source. Figure 12 b shows the polar boundary image due to this stimulus, showing how the unequal illumination of the original produces minimal effects in the oriented edge response. Consequently the filled-in surface brightness percept shown in Figure 12 d is virtually identical to that in Figure 11 c thus demonstrating a discounting of the illuminant in the surface brightness percept. In essence, the principle expressed by this model is a spatial integral (the diffusion operation) applied to a spatial derivative (the edge convolution) of the luminance image, and several models of brightness perception (Arend & Goldstein 1981, Land & McCann 1971, Grossberg & Todorovic 1988) have been proposed on this principle as the basis of brightness constancy.
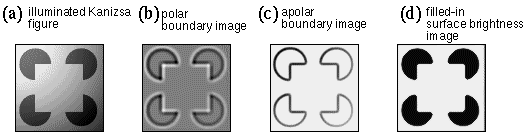
Figure 13 demonstrates the brightness contrast illusion using the same forward and reverse processing described above. Figure 13 a shows the stimulus, in which a gray square on a dark background appears brighter perceptually than the same shade of gray on a bright background. Figure 13 b shows the reified polar edge image, revealing a bright inner perimeter for the left hand square, and a dark inner perimeter for the right hand square, due to the contrast with the surrounding background. Figure 13 c shows the apolar boundary image, and Figure 13 d shows the filled-in surface brightness percept, which is consistent with the illusory effect, i.e. the square on a dark background is reified perceptually as brighter than the square on the bright background.

Figure 14 demonstrates the Craik-O'Brien-Cornsweet illusion, again using the same forward and reverse processing described above. Figure 14 a shows the stimulus, which is a uniform gray with a brightness "cusp" at the center, i.e. from left to right, the mid gray fades gradually to dark gray, then jumps abruptly to white, before fading gently back to mid gray in the right half of the figure. The percept of this stimulus is of a uniformly darker gray throughout the left half of the figure, and a lighter gray throughout the right half. If the cusp feature is covered with a pencil, the neutral gray of the stimulus will be seen. This illusion offers further evidence that the perception of surface brightness depends on the edges, or brightness transitions in the stimulus, which promote a diffusion of brightness signal throughout the regions separated by those transitions. The filled-in surface brightness image shown in Figure 14 d shows how this effect too is replicated by the model.

The regions of darker and lighter gray produced in this simulation, and the previous brightness contrast simulation appear much exaggerated relative to the subtle difference in tone observed subjectively. In the first place these illusions are somewhat dependent on spatial scale, for example the brightness contrast effect is more extreme when viewing a tiny gray patch against a white or black background. Furthermore, the simulations presented here are intended to demonstrate the computational principles active in perception, rather than the exact parametric balance to produce the proper brightness percept for all of the phenomena modeled.
The effects of the illusory contours, absent from the filled-in percept of Figure 11 c, can be added to the simulation by simply coupling the cooperative layers into the feedback loop, as explained below. Figure 15 c shows the polar cooperative image computed by feed-forward convolution, as shown also in Figure 8. A reverse convolution back through the same cooperative filter transforms this cooperative representation back to a reified cooperative representation in the oriented edge layer, as shown in Figure 15 b. Due to the symmetry of the cooperative filter, this image is not very different from the original cooperative image, being equivalent to a second pass of forward convolution with the cooperative filter, which simply amplifies the spreading in the oriented direction, and the thinning in the orthogonal direction. Next, a reverse-convolution is performed on this oriented edge image through the original oriented filter to produce a reified oriented image as shown in figure 15 a, this time complete with faint traces of the polar illusory contour linking the inducing edges. A summing of the oriplanes of this image produces the polar boundary image with cooperative influence. At the same time, a similar reification is performed in the apolar data stream, to produce the apolar boundary image with cooperative influence, shown in Figure 16 b. Finally, a surface brightness filling-in is performed using these two boundary images to produce the final modal percept which is shown in Figure 16 c. We now see the effects of the polar cooperative processing at the lowest level brightness percept in the form of a faint illusory figure whose surface brightness is explicitly represented as a brightness value throughout the illusory figure, as required for a perceptual model of the Kanizsa figure.
The general principle illustrated by this algorithm is that perception involves both a bottom-up abstraction or extraction of transients in the input, and a complementary top-down reification that fills-in or completes the percept as suggested by the extracted features. In fact, Gestalt theory suggests that these bottom-up and top-down operations occur simultaneously and in parallel, so that the final pattern of activation in each layer of the hierarchy reflects the simultaneous influence of every other layer in the system. In fuzzy logic terms the spatial interactions within each representational level, such as the cooperative filtering in the cooperative level and the oriented competition in the oriented level, express spatial inferences based on the patterns of activation at those levels, and these inferences can be propagated to other levels in the hierarchy after application of the appropriate inter-level transform. Note how the disturbing star-shaped artifacts apparent in Figure 16 b are much diminished in the corresponding surface brightness percept in Figure 16 c because they do not define enclosed contours, and therefore any brightness difference across these open-ended contours tends to cancel by diffusion around the open end. However where these extraneous contours do form closed contours, they block the diffusion of brightness signal and produce artifacts. This can be seen for example on both sides of the illusory edge of the square in Figure 16 b where the extraneous contours from the adjacent pac-man figures from opposite sides intersect, and thereby capture the diffusion of the darkness signal from diffusing smoothly into the background portion of the figure, resulting in a local concentration of darkness just outside of the illusory contour in Figure 16 c. Similarly, extraneous contours inside the illusory square block the diffusion of brightness signal from filling-in uniformly within the illusory square. The problems of cooperative processing revealed by these extraneous contours will be discussed in the second paper of the series (Lehar 1999 b) where these issues will be resolved using a more sophisticated model of collinear boundary completion.

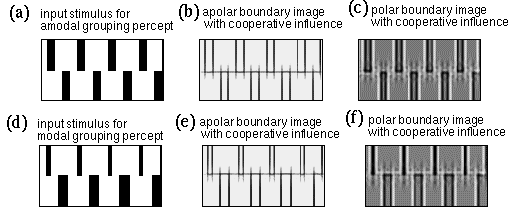
While the modeling presented above accounts for the formation of modal illusory percepts, the same model also accounts for amodal illusory grouping by producing a grouping edge in the apolar cooperative image which however produces no effect back down at the image level, because there is no contrast signal available across the contour to generate the brightness percept. Figure 17 a shows a stimulus similar to figure 2 c, and similar in principle to the camo triangle in figure 1 a. Figure 17 b shows the polar boundary image with cooperative influence, showing how the amodal contour is completed between the line endings, to produce a collinear grouping percept. The cooperative processing in the polar data stream on the other hand does not complete the same illusory contour because the contrast reversals between alternate edge stimuli cancel, as seen in the polar boundary image shown in Figure 17 c. This stimulus can however be transformed into a modal percept by arranging for a different density across the contour, as shown with the modal camo triangle in figure 2 c. Figure 17 d shows this kind of a stimulus, which produces the same kind of amodal grouping percept, as seen in the apolar boundary image in Figure 17 e, however the average contrast polarity across this contour now produces a weak horizontal polar boundary, as shown in Figure 17 f, and this polar boundary will feed the brightness diffusion to produce a difference in surface brightness in the percept across that contour.
The hierarchical architecture depicted in Figure 3 extends upwards only to the cooperative representation. However the human visual system surely extends to much higher representational levels, including completion of vertices defined by combinations of edges, and completion of whole geometrical forms such as squares and triangles, defined by combinations of vertices. The general implications of the MLRF model are that these higher featural levels would be connected to the lower levels with bidirectional connections, in the same manner as the connections between lower levels described above. Therefore as higher order patterns are detected at the higher levels, this detection in turn would be fed top-down to the lower levels, where they would serve to complete the detected forms back at the lowest levels of the representation, resulting in a high-resolution rendition of those features at the surface brightness level. It is this reification of higher order features that explains how global properties such as figural simplicity, symmetry, and closure can influence the low-level properties of the percept such as the salience of the amodal contour of the camo triangle of figure 1 a, and the contrast across the modal contours of the modal camo triangle in figure 2 d. There is an important issue concerning the reification of such abstracted high level features. The process of abstraction from lower to higher levels involves a generalization, or information compression. For example the apolar level represents an abstraction of the more reified polar edges, in the sense that each apolar edge corresponds to two possible polar edges, one of each direction of contrast polarity. Since the direction of contrast polarity information is lost in the process of abstraction, how is this information to be recovered during the top-down reification? This is a general problem wherever information that was abstracted away bottom-up must be recovered in the top-down reification. The concept of emergence in Gestalt theory suggests that the top-down processing does not proceed independently, but interacts with the bottom-up processing stream at every level of the representation. This allows missing information to be filled in from wherever it is available, either bottom-up, top-down, or laterally within the same level. The specific information that can be used for any particular reification can be deduced from fuzzy logic concepts by the general rule that if the state of activation of any node in the system is statistically predictive of the activation, or non-activation of any other node, those nodes should be connected by a mutually excitatory or inhibitory connection respectively, whose connection strength is proportional to the probability of their simultaneous activation. In the case of the reification of the apolar boundary signal, the information of contrast polarity can be recovered, if available, either bottom-up from the input, i.e. from the contrast polarity of the same edge that was abstracted upward in the first place, or laterally within the polar edge representation from other portions of the same edge as seen in figure 17 f. In other words, a strong top-down reinforcement by an apolar edge should amplify the corresponding polar edge while preserving its contrast polarity. In the absence of a local bottom-up contrast, for example at a point along the illusory portion of the Kanizsa boundary, the contrast is available laterally on the basis that a detected contrast polarity at one point along an edge is (weakly) predictive of the same contrast polarity at adjacent portions of that same edge, calculated in this case by polar cooperative processing. It is this multi-level interconnected context sensitivity that accounts for the remarkable robustness of perception in the presence of noise and ambiguity.
The principle of emergence suggests a parallel interaction between multiple local forces to produce a single coherent global state. As in the case of the soap bubble, emergence suggests that the individual particles in the system exert a mutual influence on one another by the principle of reciprocal action. This involves a bi- directional exchange of information between particles in the system. The challenge to models of visual perception has been to resolve the concept of emergence identified by Gestalt theory with the hierarchical representation suggested neurophysiologically. The general message of the present paper is that the different representational levels of the visual hierarchy are coupled by complimentary feed-forward and feedback connections that perform simultaneous forward and inverse transformations between every pair of levels in order to couple the various representations at the different levels to define a single coherent perceptual state. The implications of this view of visual processing are that the computations performed at each level of the visual hierarchy are not so much a matter of processing the data flowing through them, as suggested by a computer algorithmic view, but rather the effects of processing in any layer modulates the representation at every other level of the system simultaneously. This was seen for example in the simulations described above, where the coupling of the cooperative level into the feedback loop subtly altered the patterns of activation at all other levels simultaneously, enhancing specifically those features in the input which correspond to a cooperative edge. This behavior is comparable to the properties observed in analog circuits, in which the addition of extra capacitors or inductors at various points in a circuit subtly alters the behavior of the circuit as a whole as measured at any other point in the circuit, not only within or "beyond" the added component as suggested by a feed-forward paradigm.
The fact that the various components of the percept are experienced as superimposed is explained by the fact that the different representational levels of the hierarchy represent the same visual space. For example a location (x,y) in the apolar cooperative image maps to the same point in visual space as the location (x,y) in the surface brightness image, although the nature of the perceptual experience represented in those levels is different. The subjective experience of the final percept therefore corresponds not only to the state of the highest levels of the representation as suggested by the feed-forward approach, but rather, all levels are experienced simultaneously as components of the same perceptual experience. This approach to modeling perception does not resolve the "problem of consciousness", i.e. it does not explain how a particular pattern of energy in the system becomes a subjective conscious experience. However this approach circumvents that thorny issue by simply registering the different aspects of the conscious experience at different levels in an isomorphic representation, and therefore the patterns of energy in the various levels of the model can be matched directly to a subject's report of their spatial experience, whether the subject describes a perceived surface brightness, a perceived contrast across an edge, or an amodal grouping percept. Unlike a neural network model therefore, the output of the model can be matched directly to psychophysical data independent of any assumptions about the mapping from neurophysiological to perceptual variables.
In the interests of conceptual clarity, the visual input was described as arriving at the lowest, surface brightness level, which is also the location of the final brightness percept. However the fact that the retinal ganglion cells encode only edge information suggests that the retinal input actually corresponds to a polar boundary representation, i.e. that the processing within the retina represents an abstraction of the information at the photoreceptors, but the subsequent cortical processing of the retinal input represents a reification back to a surface brightness representation. In other words, the signal of the retinal ganglion cells can be thought of as entering the visual hierarchy mid-stream at the polar boundary level, rather than at the lowest level, from whence that information is both abstracted upwards, and reified downwards within the cortex to produce the final percept. This would explain why the subjective experience is of a surface brightness percept, whereas the retinal input is only a polar boundary signal. The concept of reification of the retinal input also explains the phenomenon of hyperacuity, i.e. the fact that visual acuity measured psychophysically appears to be of higher precision than the spatial resolution at the retina. This is because the spatial resolution at the cortical surface is greater (in millimeters of tissue per degree of visual angle) than that in the retina or in the lateral geniculate nucleus, and a lower resolution retinal image can be reified into a higher resolution cortical layer where spatial interactions like oriented competition and cooperative processing serve to focus and refine the edges at the higher resolution.
The kinds of computational transformations revealed by the perceptual modeling approach are analog field-like interactions as suggested by Gestalt theory, whose purpose is not to register detection of features, as suggested in the feature detection paradigm, but rather to generate a veridical facsimile of perceived surfaces and objects. This notion of processing by spatial diffusion operations will be elaborated in the next paper in the series (Lehar 1999 b) where the cooperative receptive field will itself be replaced by a finer grained dynamic interaction designed to account for more subtle aspects of the collinear illusory contour formation.
Arend L., & Goldstein R. 1987 "Lightness Models, Gradient Illusions, and Curl". Perception & Psychophysics 42 (1) 65-80.
Ballard D. H. & Brown C. M. 1982 "Computer Vision". Prentice-Hall, Englewood Cliffs, NJ.
Boring 1933 "The Physical Dimensions of Consciousness". New York: Century.
Dennett D. 1991 "Consciousness Explained". Boston, Little Brown & Co.
Dennett D. 1992 "`Filling In' Versus Finding Out: a ubiquitous confusion in cognitive science". In Cognition: Conceptual and Methodological Issues, Eds. H. L. Pick, Jr., P. van den Broek, & D. C. Knill. Washington DC.: American Psychological Association.
Grossberg S, Mingolla E, 1985 "Neural Dynamics of Form Perception: Boundary Completion, Illusory Figures, and Neon Color Spreading" Psychological Review 92 173-211.
Grossberg S, Todorovic D, 1988 "Neural Dynamics of 1-D and 2-D Brightness Perception: A Unified Model of Classical and Recent Phenomena" Perception and Psychophysics 43, 241-277.
Hubel D. H. 1988 "Eye, Brain, and Vision". New York, Scientific American Library.
Koffka K. 1935 "Principles of Gestalt Psychology". New York, Harcourt BraceI.
Land E. H. & McCann J. J. 1971 "Lightness and Retinex Theory". Journal of the Optical Society of America 61 1-11.
Lehar S. & Worth A. 1991 "Multi-resonant boundary contour system" Boston University, Center for Adaptive Systems technical report CAS/CNS-TR-91-017.
Lehar S. 1999 a "Computational Implications of Gestalt Theory I: A Multi-Level Reciprocal Feedback (MLRF) to Model Emergence and Reification in Visual Processing". Submitted Perception & Psychophysics.
Lehar S. 1999 b "Computational Implications of Gestalt Theory II: A Directed Diffusion to Model Collinear Illu- sory Contour Formation". Submitted Perception & Psychophysics.
Marr D, 1982 "Vision". New York, W. H. Freeman.
Michotte A., Thinés G., & Crabbé G. 1964 "Les complements amodaux des structures perceptives". Studia Psy- chologica. Lovain: Publications Universitaires. In Michotte's Experimental Phenomenology of Perception, G. Thinés, A. Costall, & G. Butterworth (eds.) 1991, Lawrence Erlbaum, Hillsdale NJ.
Müller G. E. 1896 "Zur Psychophysik der Gesichtsempfindungen". Zts. f. Psych. 10.
O'Regan, K. J., 1992 "Solving the `Real' Mysteries of Visual Perception: The World as an Outside Memory" Canadian Journal of Psychology 46 461-488.
Parent P. & Zucker S. W. 1989 "Trace Inference, Curvature Consistency, and Curve Detection". IEEE Transac- tions on Pattern Analysis & Machine Intelligence II (8).
Spillmann L. & Werner J. S. 1990 "Visual Perception- the Neurophysiological Foundations". Academic Press Inc. San Diego.
Walters, D. K. W. 1986 "A Computer Vision Model Based on Psychophysical Experiments in Pattern Recognition by Humans and Machines", H. C. Nusbaum (Ed.), Academic Press, New York.
Zucker S. W., David C., Dobbins A., & Iverson L. 1988 "The Organization of Curve Detection: Coarse Tangent Fields and Fine Spline Coverings". Proceedings: Second International Conference on Computer Vision, IEEE Computer Society, Tampa FL 568-577.