Plato's Cave: The Bubble Model
The Bubble Model
The three-dimensional visual world is projected onto the
two-dimensional retina (the optics problem). Perceptual
filling-in can be considered as a direct implementation of the
inverse optics problem, i.e. expanding the two-dimensional
retinal projection into a solid three-dimensional model. In the case
of
binocular vision
this problem is more straightforward because the depth information is
explicitly present. Spatial perception however also works on just
monocular input, which is a far more formidable and challenging
problem. The bubble model is designed therefore to work on either
monocular or binocular input, using the same fundamental principles to
reconstruct the most reliable three-dimensional percept.
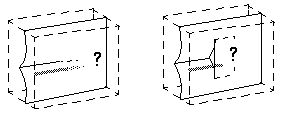
A stimulus of a tri-angular vertex as shown below (left) stimulates a
percept of a corner of a cube, or the intersection of three surfaces,
either convex or concave, as show below (second figure). Consider the
problem in terms of perceptual modeling, i.e. consider the appearence
of the percept itself, rather than the neural mechanism which
subserves that percept. An analog Gestalt model for this percept
might be something like a piece of paper creased in three folds,
corresponding to the three visual edges, which break the stiffness or
resistance to bending along those edges, as shown below (third
figure). This would tend to make the paper "pop" into either a convex
or concave corner.

Extending this idea still further, consider the computational
mechanism depicted to the right, of a solid block of perceptual
substrate which represents a slice of the visual world. Let us
suppose that the "cells" or elements of that tissue can be in one of
two states, either transparent or opaque, representing the presence or
absence of a surface at that location and depth in the visual field.
Collinearity and coplanarity constraints can be added to the behavior
of this system as
local interactions
such that when a cell is "active" or "opaque" at a certain depth, and
detects neighboring active units, it will tend to propagate its
activation to other cells in the same plane as it finds most of its
neighbors in, while inhibiting activation in the direction orthogonal
to the plane. Given such a system in an initially random state, a
smooth planar surface will tend to emerge dynamically, with dynamics
similar to a soap bubble. The coplanarity constraint will offer the
surface a certain dynamic "stiffness" or resistance to kinking of the
surface, so as to make it bend into smooth curves.
A visual edge in a two-dimensional image is constrained in X
and Y, but is undetermined in the depth dimension Z.
Therefore in the inverse optics projection, the visual edge is inverse
projected from a line to a plane in depth, in order to overlie all
points in space that represent a possible location of that line in
depth. In the example above, the image of the tri-angular vertex is
inverse projected from the front (near) surface of the block producing
three intersecting planes of influence backwards through the depth of
the perceptual block, as suggested by the gray planes in the figure
above (right).
In order to generate the proper percept, these planes would have to
influence the behavior of active units in the block so as to relax
their coplanarity constraint. This way the perceptual surface would
have a tendency to kink or fold at locations where it intersects the
inverse projection of a visual edge. Additional local interactions
could be defined in order to make the surface tend to fold in
right-angled corners.
In other words, it is possible to define a Gestalt-like analog dynamic
mechanism which would respond to a visual input like the one shown
above by constructing a three-dimensional reification of the
percept. The exact implementation is not as important as the fact
that it is certainly possible to define a system with the
required properties, and that system would correspond more closely to
the actual percept than any of the conventional models
proposed to account for vision. The orthogonality
constraint, or tendency for the surface to fold at right angles
would be a natural property of a system defined in orientational
harmonics.

Given a single local edge therefore, the system would tend to pop into
one of the configurations shown above: a convex corner, a concave
corner, or the edge of one surface occluding another (two possible
configurations). Given only the local information, the system has no
way of knowing which is the correct interpretation. Given more global
information however, the forces in neighboring regions will influence
the outcome at this local region as will be described below. The
system must therefore be able to "pop" between equally likely
alternatives in a multi-stable manner, like
the Necker cube
until more global evidence is acquired. Indeed the multi-stable
nature of percepts like the Necker cube provide strong evidence for
this kind of reification mechanism.
Collinear Completion
In the Directed Diffusion model I introduced the notion of edges
propagating in a collinear fashion by a spatial diffusion mechanism.
In this three-dimensional extension to that idea, the edge is more
like a fold or crease in a physical surface. The dynamics must be
arranged so as to propagate such creases in a collinear manner through
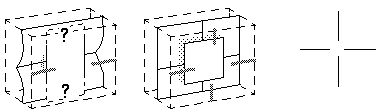
regions of no input. For example an edge which fades away will create
such a crease which will tend to propagate in the manner of a crack in
a physical surface, as suggested below (left). The propagation of
this crack will be greatly influenced by contextual cues, for example
the presence of a crack growing from the opposite direction, or
perhaps the presence of a texture of multiple visual edges which will
weaken the perceptual surface in a certain direction. A visual edge
which terminates abruptly on the other hand suggests an occluding
surface. again, this behavior can be programmed into the model by
defining the right set of local dynamics, as shown below (right),
where the strong edge directly adjacent to a strong absence of an edge
creates a local stress in the perceptual surface which would tend to
make the crack propagate behind the occluding surface, thus
elevating it up away from the original surface. The other boundaries
of this surface however remain unconstrained, and therefore produces
no percept of its other edges.
The presence of an abrupt line ending on the other side of
this figure however would tend to complete the propagation of the
crack behind the occluding surface, which would tend to
further elevate the occluding surface over the occluded edge, while
producing an amodal percept of an edge occluded by a nearer
surface, as shown below (left). In the presence yet of another pair
of abruptly terminating vertical lines, the occluding surface will be
surrounded on four sides, which will induce it to pop into
the foreground as a separate surface, while producing an amodal
percept of an occluded cross behind that surface. This would
explain the appearence of the Ehrenstein figure shown below (right),
as well as providing an explanation for the Gestalt principle of
closure.
The exact dynamics and details of this model have not been fully
worked out. But the principle behind this mechanism is
clear, and it is also clear that such a system is possible in
principle to define. It is also clear (at least to me) that this kind
of a system captures the subjective impression of these illusory
figures in a very compelling way.
Return to argument
Return to Steve Lehar




