Plato's Cave: The Bubble World
The Bubble World
The Bounded Percept
The parable of Plato's Cave suggests that the world you see around you
is a percept inside your head. The model I have presented thus far is
a
fully spatial
model, i.e. its surfaces and volumes are represented as surfaces and
volumes, somewhat like an architect's model, standing in the lobby of
the building of which it is a miniature copy. But an architect's
model must of necessity be of finite size, which is generally achieved
by establishing abrupt limits beyond which the model is no longer
defined. Such abrupt limits are not seen in the spatial percept of
surrounding space, and yet at the same time the perceptual space
appears bounded. The following figure illustrates this point.
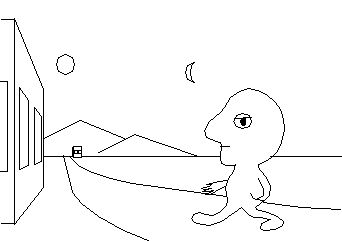
While the space near the body appears to be approximately Euclidean,
such as the building in the foreground, objects in the distance appear
strangely foreshortened, so that the sun and moon and distant
mountains all appear to be at about the same perceptual distance from
the observer, although geometrically the mountains are orders of
magnitude closer than the moon, which in turn is orders of magnitude
closer than the sun. The sun and moon appear as flattened disks, and
the mountains appear in silhouette almost as if cut out of cardboard
and pasted against the dome of the sky.
Objects between the observer and the mountains gradually become more
flattened with distance from the observer, as seen in the building in
the background, whose depth is seen with less resolution than are its
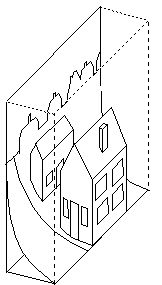
height and width. This phenomenon is reminiscent of dioramas,
illustrated below, as seen in museum exhibits, where a
three-dimensional foreground model is displayed in front of a
two-dimensional background painting, with a smooth transition in
between the two representations, creating the impression of a full
three-dimensional scene. In order to create the smooth transition, the
depth dimension of the spatial models is progressively reduced with
proximity to the backplane painting. The fact that these displays
create such a vivid sensation of depth suggests that this
representation is meaningful to human perception.

Bounding in Depth
This kind of mapping can be defined mathematically with a
vergence representation
which, when applied to the bubble model discussed above, results in a
representation like the one shown below, where surfaces and volumes
are represented in a fully spatial manner, while the spatial
resolution of depth approaches zero as distances approach infinity.
Boundary completion and surface filling-in can be computed spatially
in this representation, which nevertheless is bounded in the depth
dimension.
Bounding in All Three Dimensions
In order to bound the representation in the other two dimensions, the
X and Y of Cartesian coordinates can
be replaced by azimuth and elevation angles in polar coordinates,
which are also bounded dimensions. All three dimensions of this
spherical representation are closed, or bounded, which means that the
boundless infinity of Euclidean space can be remapped within a finite
sphere in an angle / angle / vergence representation, with the
ecological advantage that the most important region of space, that
closest to the body, is mapped at the highest resolution, while the
least significant region is mapped at the lowest resolution.

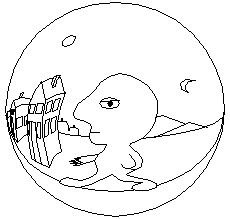
The figure below illustrates how such a representation would reflect
the percept of a man walking down the road.
Boundary and Surface Completion in 3-D
In order to perform boundary completion and surface filling-in in the
manner described in the Bubble Model above, the geometrical
distortions of the perceptual representation must be applied to the
boundary and surface completion operations. Consider again the
two-dimensional case of the Kanizsa figure depicted below (left) whose
illusory square emerges by collinearity interactions between the
visible edges of the inducing pac-man figures. In the Directed
Diffusion model this completion by collinearity is mediated by a
matrix of oriented edge sensitive cells, represented by the short
black lines below (center), whose activation diffuses along lines of
collinearity, represented by the long gray lines below (center).
These lines therefore represent a grid or reference frame of
collinearity. For example the figure below (right) represents the
response of the matrix below (center) to the Kanizsa stimulus below
(left).

In order to extend this idea to three dimensions, the matrix of cells
must be expanded to solid volume of cells, as shown below, where the
neural connectivity defines a three-dimensional web of colinearity in
all directions through every point in the volume. The percept of a
cube in this representation for example would be defined by the
activation of oriented cells at the eight corners of the cube
representing vertices with three mutually orthogonal edges that meet
at the corner, as well as by lines of activation connecting the
corners along the sides of the cube, and planar activation connecting
the sides along the faces of the cube.

Applying the angle / angle / vergence transformation to this infinite
cartesian grid of collinearity connections produces the bounded
spherical volume of tissue shown below, where the central point
represents the center of the head, and the spherical surface
represents perceptual infinity. This distorted grid is like a
perspective view of the infinite Cartesian grid above, and, by the
laws of perspective, all lines that are locally parallel meet at a
point at perceptual infinity in both directions. This distorted grid
performs an
inverse perspective
transformation on the visual input, allowing veridical judgements of
colinearity to be made on an image containing perspective distortions.
Notice that this representation is approximately Euclidean near the
center, for instance within the central bulging square below, and
becomes progressively more distorted near the surface of the sphere.
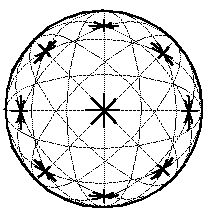
The idea of this distorted reference grid is that points of neural
activation in this system will appear to be perceptually colinear when
they fall along one of the curved lines in the figure. In other
words, this system represents perceptual collinearity by a
set of curves which become progressively more distorted as
they approach infinity, at the surface of the sphere. Notice also
that the perception of orthogonality also experiences a similar
distortion. Edges which are perceived as orthogonal are also
geometrically orthogonal at the center of the representation, but are
squashed into greater or lesser angles near the edge of the space, as
shown below. The "90 degrees" caption in the figure refers to the
perception of orthogonality for edges in the representation
that meet at the angles shown.

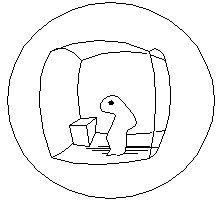
The figure below shows how such a system would represent a cubical
room to an observer at the center of that room. The lines which
define the boundaries of each wall bulge outwards from the observer,
and yet they follow lines of colinearity as shown above, and thus
produce a percept of straightness. The corners of the room are
similarly distorted, but again they conform to perceptual
orthogonality as defined by the lattice of connectivity, and therefore
are perceived as orthogonal corners.
Consider again now the percept of a man walking down a road. This
figure shows how the infinite dimensions of the outside world can be
captured inside a perceptual bubble of finite dimensions. Notice how
the perceptual image of the road appears locally parallel near the
man's feet, but converges to a point up ahead and behind. Because the
edges of the road generally follow the grain or texture of the matrix
of connectivity in the perceptual mechanism as shown above, the man
judges the sides of the road to be parallel, even though paradoxically
they appear to meet at a point both ahead and behind. Likewise, the
vertical walls of the house seen below seem to bend away from the man
in the perceptual representation, but again they generally follow the
grain of collinearity representing vertical edges, which converge to a
point vertically above and below, and therefore they appear to the man
to be parallel to one another and vertical, just as in the example of
the percept of a cubical room shown above. The angles of intersection
between the vertical walls and the horizontal ground are similarly
distorted in the perceptual representation, but conform to
orthogonality in that representation and are therefore perceived as
orthogonal.

Return to argument
Return to Steve Lehar











