Plato's Cave: The Lighted Bubble World
The Lighted Bubble World
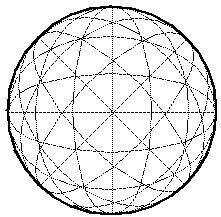
The architecture of connectivity for the perceptual sphere proposed by
the Bubble World model has some interesting geometrical properties
that suggest a solution to the problem of lightness, brightness, and
form perception. Every point on the surface of the sphere is
connected by the texture of colinearity through every point in the
volume of the sphere, and the angle at which those lines of
collinearity pass through a point within the sphere depends only on
the location of the surface point on the sphere. This property
follows from the fact that a point on the spherical surface represents
a specific direction in space, and all parallel lines
pointing in that direction in Euclidean space will pass through that
point on the spherical surface in perceptual space.
Imagine therefore that this same texture of connectivity is designed
to carry brightness information. A "light source" at a point on the
spherical surface will thereby create a percept of illumination from
the corresponding direction in space. Likewise reciprocally,
illumination on the "sunny side" of all perceived objects in the space
will be communicated in the opposite direction to create the percept
of an illuminant in the opposite direction. In such a system a
perception of any object will automatically produce a percept of an
illuminant, which in turn will produce an expectation of illumination
for other objects in the space.

Specifically, every point on a perceived surface must represent or
encode two values- the perceived brightness of that point, i.e. how
much light appears to be reflected from that surface, and the
perceived reflectance or "lightness" of the surface, i.e. the "color"
it is perceived to be "painted". An important function of the visual
system is to factor these two quantities in order to distinguish
lightness edges from illuminance edges. In the
Lighted Bubble Model
this is achieved by giving these two variables different properties of
spatial interaction- the "lightness" value tends to diffuse across
surfaces in space creating a uniform percept even around corners,
while the reflected light is expected to be greater on surfaces facing
the illumination source.
Consider the ambiguous figure below. If it is perceived as a flat
figure of two diamond shapes, both shapes are facing the same
direction in space, and therefore they project contradictory
information about the illumination from that direction, one suggesting
a lighter, and one a darker light source. The light source value thus
takes on an intermediate value. The difference in brightness must
therefore be accounted for by a difference in surface reflectance,
therefore the lightness variable takes on different values across the
central edge.
Alternatively, the figure can be perceived as a three-dimensional
figure of a single folded surface, which in the absence of
contradictory evidence might be supposed to have uniform lightness.
The "lightness value" would thus tend to propagate throughout the
surface even crossing the fold in the middle. The difference in
brightness seen on the two faces therefore would suggest a difference
in illumination due to the geometrical fold, which can be perceived as
either a concave or a convex corner. A concave interpretation
suggests a light source from the right, whereas a convex
interpretation suggests a light source from the left.

The Lighted Bubble model suggests that as this percept pops in a
bistable manner between the two alternative interpretations, it also
alternately "turns on" a supposed light source on the appropriate
side. That light source in turn "illuminates" all other perceived
objects in the space, changing their expected brightness
value in a geometry-dependent manner, i.e. they are expected to appear
brighter on the sunny side, and less bright on the shady side. This
effect is seen in the figure below, where the single block which lacks
shading on the left side is perceived to have a "lighter paint" on
that side than the other blocks, and this white side even appears
lighter than the white top of the block, which is actually the same
color.

The interaction between the brightness and form perception goes in
both directions, as can be seen in the example below, where the
presence of a single unambiguous feature in a field of ambiguous ones
is sufficient to establish with certainty the direction of
illumination which, in turn, establishes with certainty which of the
two alternative spatial interpretations is valid.

The important principle embodied in this model is that the complex
geometrical interactions between perceived form and illuminant are
modeled by a system which replicates those same geometrical
properties, and thus need not calculate geometrical abstractions, but
simply performs a parallel "ray tracing" to render the required
percept in a three-dimensional context..
Return to argument
Return to Steve Lehar





