Plato's Cave: Motion in the Bubble World
Motion in the Bubble World
The Bubble World model addresses the problem of motion perception in
the same manner as it addresses all problems, by reifying all
possible interpretations of the sensed phenomenon, and then choosing
from that multitude of percepts the one which represents the simplest
percept.
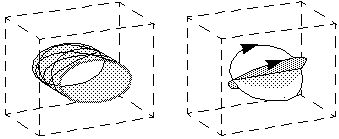
Consider a single visible point rotating about an invisible axis, so
as to produce the two-dimensional sensation of a point travelling
around an ellipse. The first step is to inverse-project this ellipse
onto the face of a block of perceptual tissue, as shown below. This
will produce a stimulation of motion perception throughout the surface
of an elliptical cylinder through the depth of the perceptual block,
as suggested below right.

This motion signal is also consistent with a number of
alternative cyclic motions around the surface of the elliptical
cylinder which are not parallel to the ellipses on the front
and rear surfaces of the block, as suggested below (left). Among
these multiple possible cyclic motions are two special cycles which
happen to form perfect circles in depth, whose two-dimensional
projection coincides exactly with the original ellipse, as shown below
(right). The visual system seems to have a preference for perceiving
rigid rotation, and since these two motions are the only ones
consistent with rigid rotation, they constitute the most likely, or
simplest three-dimensional perceptual hypothesis of the
two-dimensional elliptical rotation.
The special circular symmetry of these two cycles can be best detected
and recognized by a cell located at the three-dimensional center of
these circles within the volume of the perceptual tissue. I cannot
say exactly how such a cell would recognize this circular
motion except to suggest some form of harmonic resonance, which might
define the center of symmetry of the two rotations.
The above explanation applies not only to full circular motion viewed
in perspective, but also to any circular motion through an arc, which
will be likewise perceived as a circular rotation about a central
axis. If more points are seen rotating about the same axis, the
percept of the rotation will become even more pronounced, and if some
points are seen to disappear by occlusion behind the rotating body,
this will eliminate one of the two alternative rotation axes,
resulting in a stable percept.
Although the details this explanation remain somewhat vague, this
model does propose certain specific principles of perception:
-
The three-dimensional percept is reconstructed from the
two-dimensional stimulus in a fully spatial context.
-
The principle behind this reconstruction is to simultaneously
reconstruct all possible paths, and then to choose from
those the most likely (simplest) alternatives.
- The recognition of the special symmetry of the rigid rotations
is greatly simplified by performing the recognition in a
three-dimensional context, where those rigid rotations are actually
circular.
-
After selection of the most likely alternative, a feedback interaction
suppresses all less likely alternatives, while enhancing
the most likely alternatives.
-
The result of all this manipulation is a complete reification of the
perceived motion in as much detail as possible, including a
filling-in of invisible surfaces and volumes wherever they are
supported by the evidence.
It will be seen that these are the same general principles seen
throughout this approach to perception.
Return to argument
Return to Steve Lehar


