Plato's Cave: Where in the Brain
Where in the Brain
I have described a spherical computational structure with a specific
pattern of connectivity. Where in the brain might such a structure be
located?
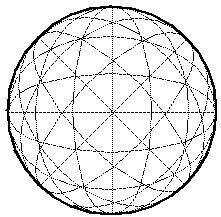
Beginning at the lower end of the phylogenetic tree, the computational
structure depicted above might correspond to the spherical structure
seen at the center of the insect visual system, where the base of the
ommatidia meet. This model predicts therefore that neural connections
in the insect visual system will be found in a pattern as shown above,
designed to perform boundary and surface completion in
three-dimensions. A significant feature of this representation is
that it would represent not only the visible part of the visual field,
but would also have a representation for the part of the world beyond
the visual field, or occluded by the insect's own body, even if that
sector is not covered by omatidia facing in that direction, and that
collinear completion (e.g. of the horizon line) would occur across
these blind sectors. This hypothesis is testable in principle.
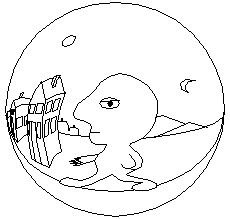
In human vision no such spherical structure is apparent. The structure
need not however be physically spherical, it need only be
computationally spherical. For example, the sphere represented above
might be opened up at the back and stretched out into a flat circular
disk, as suggested below,
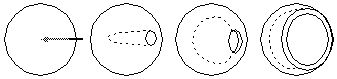
i.e. by inserting a vector from the posterior point in to the center
of the sphere, and then stretching the resulting cavity outwards
towards the surface of the sphere, resulting in a flattened, partially
spherical surface with a finite thickness. The result of this
topological transformation is shown below, where the inner surface of
the perceptual sphere, representing the surface of the head, would
correspond to the near face of the disk, and the outer surface of the
sphere representing perceptual infinity would correspond to the far
surface of the disk, while the thickness of the disk would correspond
to perceptual depth. A face is sketched on the near surface of the
disk in the figure to indicate that this surface represents the
surface of the face, while the rest of the body appears in perspective
at the bottom, beyond the cross-section of the neck, shaded with
hatched lines in the figure. The outer rim of this perceptual disk
represents all of space behind the observer, and the entire line of
the outer perimeter represents the single point directly behind the
man's head. The road which stretches to the horizon behind, stretches
to the periphery of the disk to the right and left, disappearing as it
reaches the perimeter of the disk on both sides.

If the neural connectivity were preserved topologically across this
geometrical transformation, the computational properties of this flat
disk would be identical to that of the perceptual sphere. On the
other hand, a less topological transformation would result in a loss
of perceptual resolution in depth relative to azimuth and elevation,
and perhaps a nonlinear loss of resolution to the posterior hemisphere
of space relative to the anterior half, as is seen in the visual
cortex. Indeed, this structure now begins to resemble the mapping of
the primary visual cortex.
The next figure shows how this transformation would affect the shape
of the body map within the spatial map, inflating the face while
shrinking the body.

Notice that in this model, an integral part of the representation of
space is a representation of the body surface, as suggested by the
[spatial robot analogy]
which would be represented in the same manner as any other surface in
the world, except of course that it would be updated both visually and
through somatosensory signals. The phantom limb phenomenon
experienced by certain amputees suggests how a somatosensory signal
can generate a spatial representation of a limb in the absence of
visual confirmation. This portion of the model would presumably
correspond to the somatosensory cortex which represents a spatial map
of the body surface.
Two issues remain to be resolved: what about the higher cortical maps
in V2, V3, IT, and other areas, and how is this mapping affected by
rotation of the eyes, rotation of the head, or rotation of the body?
For this model suggests that a rotation of the body should result in a
counter-rotation of the "image" of the external world relative to the
perceptual sphere. On the other hand, if recognition of objects in
the world corresponds to the activation of object recognition cells,
this shifting image of the world must somehow be anchored, if those
cells are to have a fixed location in the brain.
A solution to this problem was suggested earlier in the discussion of
the
[invariant representation]
where it was shown how the presence of a pattern of activation in a
matrix of cells can stimulate a global cell in a rotation,
translation, and scale invariant manner. In the Bubble World model,
this argument can be extended into three dimensions by way of
spherical harmonics
in the perceptual sphere, which can define three-dimensional forms in
an invariant manner. For example an eight-way vertex in spherical
harmonics would define an eight-pointed shape at a higher level, which
would complete by boundary and surface filling-in at the lower levels
to an eight cornered cube, as suggested below. The cube would be
encoded by a resonator (i.e. tuned filter / oscillator) tuned to the
frequency which would promote the emergence of this eight-way harmonic
in the perceptual sphere in a rotation, translation, and scale
invariant manner.

Return to argument
Return to Steve Lehar






