| Back | Return to Beginning | Next |
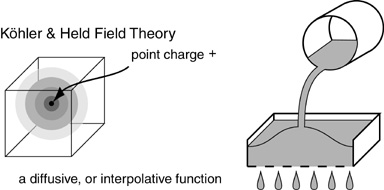
Wolfgang Köhler proposed a representation based on electric fields, like the electric charge that distributes itself uniformly across the surface of a charged object. This is a promising start, because electric fields are not discrete units, but spatially continuous interpolative structures that can be stimulated by a point charge at the center. For example one could imagine a volumetric substrate in which a point charge applied at the center would generate a complete surrounding field around that point. A threshold set on that field would define an abrupt spherical surface whose radius can be adjusted by varying the threshold, or by varying the intensity of the central charge.

But the distribution of electric charge is a simple interpolative function, similar to the principle by which water seeks its own level in a vessel, or perhaps a viscous liquid like honey, which would produce a similar surface gradient when honey is applied to the central point (while draining constantly from below).
If you want to define more complex structures besides simple spheres, you would have to apply the central charge in a more complex pattern. For example to create an image shaped like a hand would require charge to be applied along the central skeleton of the hand shape, from whence the interpolative field would "fill out" the full volumetric percept.

But that merely begs the question what kind of mechanism would "paint" the pattern of that central skeleton? Simple diffusive or interpolative functions cannot produce that kind of structured pattern, while neural projective fields run lead again to a combinatorial explosion.
| Back | Return to Beginning | Next |