| Back | Return to Beginning | Next |
I propose a small variation to Köhler's electric field theory. I propose that instead of static electric fields, the brain employs dynamic oscillating electric fields in the form of electrochemical standing waves across the neural substrate.
Harmonic resonances are a natural property of all physical systems. They are seen in the vibration of elastic solids, acoustical harmonics in resonant cavities, harmonic oscillations in electrical and electronic circuits, lasing and masing in electromagnetic radiation, and even in chemical reactions in the form of reaction diffusion.
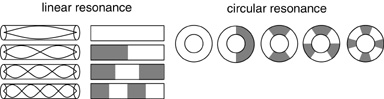
A fundamental property of all such harmonics is that they tend to divide the resonating body into integer numbers of equal intervals in a periodic or symmetrical pattern. For example the figure on the left (below) shows the patterns of acoustical oscillation in a closed tubular cavity as it resonates to the first, second, third, and fourth harmonics. This figure could also be considered as a depiction of the modes of oscillation of an elastic rod.

The figure on the right illustrates the corresponding acoustical harmonics in a circular tube, or vibrational harmonics in a ring which likewise subdivides the circle into segments of equal angular extent. Unlike in the case of the linear harmonics which are fixed by the boundary conditions at the ends of the tube, the circular harmonics can occur at any orientation.
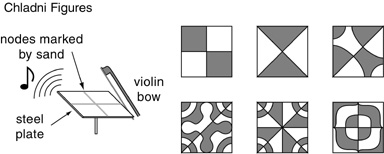
Moreover, the patterns due to harmonic oscillation are not always a simple linear periodicity. Chladni showed how a steel plate that is set into harmonic oscillations by bowing it with a violin bow can exhibit a large variety of harmonic modes whose geometrical patterns can be revealed by a sprinkling of sand, which collects at the nodes of vibration. The next figure illustrates just some of the many standing wave patterns that occur in a square plate bowed in this manner.
| Back | Return to Beginning | Next |