[This section of the Directional Harmonic Theory paper as originally submitted was removed by order of Reviewer #2, although I contend that it is one of the most interesting and significant aspects of the paper and a central part of the argument.]
The dynamic neural network is not really a single mechanism, but a set of specialized mechanisms, one for each distinct type of behavior required of the system. What is required for a more plausible model of illusory contour formation is a single mechanism or computational principle to account for all of the diverse completion phenomena, in order to escape the combinatorial problem inherent in neural network approach. Whatever its shortcomings as a model of neurophysiology, the DNN concept does nevertheless serve a useful purpose as a perceptual model, i.e. a quantitative description of the functional principles behind certain perceptual completion phenomena, to specify the functional objective, or target behavior of an adequate model of these phenomena. One of the most appealing aspects of the DNN paradigm from the Gestalt perspective is the idea of the visual system as a dynamic mechanism capable of producing an infinite variety of spatial patterns, but with a built-in spatial bias that tends to promote particular types of patterns. Such a system will naturally tend to "interpret" a visual input in terms of those pattern primitives. Driving the system with a random noise input brings out the eigenfunctions, or preferred patterns of response of the system, which in turn reveal the structural primitives of the visual code. For example the eigenfunctions of the center- surround DNN define a pattern of spots of a certain size and average spacing, as seen in figure 6 B, while those of the collinear DNN define patterns of stripes, or parallel contours, as seen in figure 7 B and C.
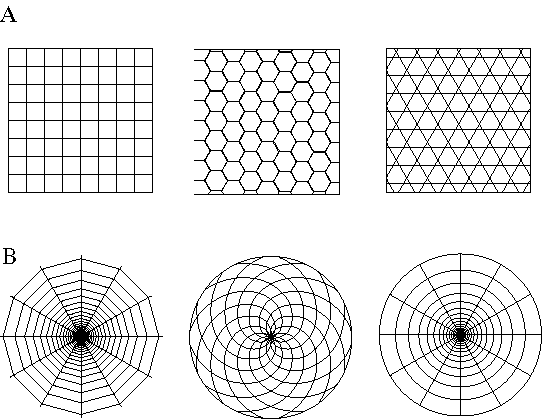
Seen in this light, the Gestalt laws of perceptual grouping, i.e. the tendency to perceive regularities in the form of good continuation, symmetry, periodicity, prägnanz, etc. can be seen as evidence for the eigenfunctions of visual perception. Further evidence comes from studies of the psychedelic experience. One of the characteristic properties of intoxication by hallucinogenic substances such as LSD and Mescaline is a tendency to spontaneously perceive regular geometrical forms. Heinrich Klüver (1966) has categorized certain types of patterns, or form constants, commonly observed under mescaline intoxication, which subjects described as lattice, fretwork, filigree, honeycomb, and chessboard patterns, as suggested in figure 8 A, as well as cobwebs, tunnel and funnel patterns as suggested in figure 8 B. These same form constants are also commonly observed under a wide variety of conditions of psychological stress, or threshold consciousness, including falling asleep, waking up, insulin hypoglycemia, the delerium of fever, epilepsy, psychotic episodes, advanced syphilis, sensory deprivation, photostimulation, electrical stimulation, crystal gazing, migraine headaches, dizziness and a variety of drug intoxications (Siegel 1976). The diversity of different conditions which provoke the same kinds of patterns suggests that these form constants reflect some fundamental property of the visual system.

Form constants reported under intoxication by mescaline which are described as (a) lattice, fretwork, filigree, honeycomb, and chessboard patterns, and (b) cobweb, tunnel, and funnel patterns. These same form constants are observed under a wide variety of conditions of psychological stress, or threshold consciousness, suggesting that they are a manifestation of the eigenfunctions of perceptual processing.
Siegel (1976) observes that the visual patterns seen under LSD intoxication are strikingly similar to the primordial or archetypal forms such as the mandala, the mystic symbol of the universe employed in Hinduism and Buddhism as an aid to meditation. Moreover, as many anthropologists have noted, the hallucinogen-inspired art of many primitive peoples often contains similar geometrical patterns of form, color, and movement (Lewis-Williams & Dowson 1988). Actually, the same kinds of form constants also appear commonly in art which is not hallucinogen-inspired, most especially in the patterns of non- representational or decorative art and ornamental design. For although there is a great degree of variation in the arts of different cultures, there is also much that is common among them. Figure 9 shows some patterns of ornament from a range of different historical styles selected from Speltz (1910). Despite stylistic variations between the ornament of different cultures, all of them share certain general properties, most prominent of which are the factors of periodicity and symmetry, both in simple and compound hierarchical form, as well as lattice, fretwork, filigree, and cobweb type patterns. Further support for the psychological significance of aesthetic factors is seen in the fact that the patterns of ornament are actually idealized exemplars, or reified manifestations of the Gestalt laws of perceptual grouping. Factors such as similarity, proximity, good continuation, closure, symmetry, periodicity, and prägnanz, are prominently evident in virtually all ornamental design (Arnheim1969, 1988). In fact even representational art often exhibits these same factors, i.e. an artistic rendition of a natural object is usually characterized by more regularity, symmetry, periodicity, prägnanz, etc. than the object that it represents, and it is these very factors that contribute to the aesthetic pleasure the work invokes (Ramachandran & Hirstein 1999). These patterns of regularity and spatiotemporal order are not confined to the visual arts, but extend into every dimension of aesthetic and functional activity, including music, rhythm, poetry, dance, and architecture. More than one author has suggested that the properties that we find to be pleasing in all aspects of aesthetic activity, are pleasing exactly because those properties are easily represented in the internal code of our perceptual mechanism (Arnheim 1969, Herzberger & Epstein 1988). That the beauty in music, art, and dance reflect a similarity between the beautiful work and the natural structure of the mind. That beauty is perceived in objects which are complex enough to fully engage our perceptual system without overloading it with excess complexity, and when that complexity is expressed in a form that is naturally and efficiently encoded by our perceptual mechanism (Sander 1931). This might be called a psycho-aesthetic hypothesis.

Patterns of ornamental design, selected from Speltz (1910). Despite stylistic variations between the ornament of different cultures, all of them share certain general properties, most prominent of which are the factors of periodicity and symmetry, both in simple and compound hierarchical form, as well as lattice, fretwork, filigree, and cobweb type patterns as seen under intoxication by hallucinogenic substances. I propose that these patterns reflect the eigenfunctions of the visual system.
If the psycho-aesthetic hypothesis is correct, then the principle can also be inverted, to deduce the properties of the perceptual representation by the common properties observed in human art across cultures. Specifically, a mechanism whose eigenfunctions correspond to the kinds of patterns observed in visual hallucination, ornament, and artistic design, is one that has captured some essential aspect of the computational mechanism of visual perception. It is clear from the properties of hallucination patterns and of ornamental design that completion by collinearity alone is inadequate as a model of perception, because those patterns typically exhibit many different vertex types at points where the pattern lines meet or cross. However the ability to form patterns of vertices is still insufficient to capture the essential characteristics of the eigenfunctions of human vision. For the lattice, fretwork, filigree, or honeycomb patterns are characterized by a global framework that relates the local vertex elements in a larger periodic matrix, while cobweb, tunnel and funnel patterns exhibit not only periodicity, but also a global symmetry about some focal center. While it is perhaps possible to conceive of a DNN model capable of illusory vertex completion in all its various manifestations, it is much harder to imagine any kind of DNN architecture capable of this kind of spontaneous global organization, because the combinatorial possibilities are so astronomical as to preclude any kind of hard-wired receptive field solution to the problem. It is exactly this holistic or global aspect of perceptual function which was a central focus of Gestalt theory, as counter-evidence for any kind of localized or atomistic principle of perceptual computation. It can hardly be an accident on the other hand that the most prominent characteristics of patterns of ornament, i.e. symmetry and periodicity both in local and in global hierarchical form, are also natural properties of harmonic resonance, or patterns of standing waves in a resonating system.
Arnheim R. (1969) Art and Visual Perception: A Psychology of the Creative Eye. Berkeley, University of California Press.
Arnheim R. (1988) The Power of the Center. Berkeley, University of California Press.
Hertzberger B. & Epstein D. (1988) Beauty and the Brain: Biological Aspects of Aesthetics. Basel: Birkhauser Verlag.
Klüver H. (1966) Mescal and the Mechanisms of Hallucination. Chicago: University of Chicago Press.
Lewis-Williams J. D. & Dowson T. A. (1988) The Signs of All Times: Entopic Phenomena in Upper Paleolithic Art. Current Anthropology 29/2 201-245.
Ramachandran V. S. & Hirstein W. (1999) The Science of Art: A Neurological Theory of Aesthetic Experience. Journal of Consciousness Studies, 6, (6-7), 15-51.
Sander F. (1931) Gestalt Psychologie und Kunsttheorie: Ein Beitrag zur Psychologie der Architectur. Neue Psychol. Studien 8, 311-333.
Siegel, R. (1976) Hallucinations. in The Mind's Eye, Readings from Scientific American, W. H. Freeman & Co., New York, 109-116.
Speltz A. (1910) The Styles of Ornament from Prehistoric Times to the Middle of the XIXth Century. London: B. T. Batsford.