
Gestalt theory reveals a holistic global aspect of perception which is difficult to account for either in computational or in neurophysiological terms. Elsewhere I have presented a minor but significant extension to the Temporal Correlation Hypothesis (Singer & 1995, Singer 1999) in the Harmonic Resonance Theory (Lehar 1999). I propose that the synchrony observed between cortical neurons is not a signal in its own right communicated from cell to cell, but rather it is a manifestation of a larger standing wave pattern that spans the cortical region in question, and that the structure of the standing wave encodes certain aspects of the structure of the perceived object or grouping percept. This concept is elaborated here in the more specific Directional Harmonic Model, that accounts for a variety of diverse perceptual grouping phenomena that have been difficult to address using neural network concepts. Computer simulations of the Directional Harmonic model show that it can account for both collinear contours as observed in the Kanizsa figure, orthogonal contours as seen in the Ehrenstein illusion, and a number of illusory vertex percepts composed of two, three, or more illusory contours that meet in a variety of configurations.
Gestalt theory demonstrates in compelling fashion that there is something very peculiar going on in the computational processes of visual perception. For Gestalt theory reveals a holistic global aspect of perception that is difficult to account for either in computational or in neurophysiological terms. Consider for example the camouflage triangle (camo triangle) shown in figure 1 A. Any recognition algorithm that begins with local feature detection would be surely swamped by the wild profusion of local edge features present in this stimulus, in which those edges that form part of the triangular perimeter are locally indistinguishable from the other extraneous edges. This figure suggests therefore some kind of holistic principle of recognition based on the global configuration of the whole, rather than the local properties of its individual parts. However the influence of that global recognition clearly extends back down to the local feature level, because the recognition of the triangular form is immediately accompanied by the appearance in visual consciousness of a sharp well defined contour that spans even those portions of the triangle where no edge is explicitly present in the stimulus. However the computational principle behind this holistic style of processing remains largely a mystery.

(a)The camoflage illusory triangle (camo triangle) demonstrates the principle of emergence in perception, because the figure is perceived despite the fact that no part of it can be detected locally. (b) The Kanizsa illusory triangle. (c) The subjective surface brightness percept due to the Kanizsa stimulus. (d) The amodal contour percept due to the Kanizsa stimulus, where the darkness of the gray lines represents the salience of a perceived contour in the stimulus.
There are nevertheless certain operational principles that are evident in Gestalt illusory phenomena, and these principles offer an invaluable starting point for probing the inscrutable logic of the visual system. Specifically, the camo triangle demonstrates the perceptual tendency for completion by collinearity, corresponding to the Gestalt law of good continuation. For it is the collinear configuration of those innumerable local edge fragments that promote the perceptual emergence of the global edges of the triangular form. A simpler and therefore clearer example of completion by collinearity is seen in the Kanizsa triangle shown in figure 1 B. This illusory figure offers a means to explore the principles behind completion by collinearity by examining the effect of parametric variations of the inducing "pac-man" features on the perceived salience of the illusory contours (Kellman & Shipley 1991, Banton & Levi 1992). The observed properties of the Kanizsa illusion therefore offer a concrete starting point for modeling the specific spatial interactions apparent in perception. Grossberg & Mingolla (1985, 1987) have proposed a neural network model that is consistent with some of the observed properties of illusory contour formation. In their model, the principle of collinear completion is implemented by way of dynamic neural elements interacting through spatial receptive fields. Specifically, detection of a local edge in the image by an edge detector cell tends to propagate neural activation in a direction parallel to that edge, guided by specialized receptive fields whose spatial properties are tuned specifically to promote collinear contour completion.
There are however other more global aspects of Gestalt illusory phenomena which are very difficult to account for in neural network terms. In fact the original significance of these Gestalt illusions was specifically to demonstrate the inadequacy of any theory of perceptual processing that builds up from locally detected features. This principle is seen most clearly in the camo triangle, where it is the global configuration of features as a whole which determines the perception of the figure, because the illusory contour is much attenuated, or even disappears altogether, when viewing the figure through a reduction screen that exposes only a few local elements at a time. This figure therefore demonstrates the Gestalt principle of emergence, whereby the global percept is determined by a global configuration of a multitude of individual local features, none of which offers sufficient concrete featural evidence when considered in isolation. Koffka (1935) presented the physical analogy of a soap bubble to demonstrate the operational principles behind emergence. The spherical shape of the soap bubble is not encoded in the form of a spherical template, or abstract mathematical code, but rather that form emerges from the parallel action of innumerable local forces of surface tension acting in unison.
Another global effect is seen in the fact that the salience of the illusory percept is influenced by the closure of the figure as a whole, a manifestation of the Gestalt principle of closure, or the perceptual tendency to perceive complete enclosed forms. Breaking the closure of the Kanizsa triangle by removing or occluding one of its inducing pac-man features reduces the salience of the entire figure, even that portion of the illusory edge that spans the remaining pac-man features, just as a bubble surface tends to collapse when it's global closure is breached at any point. Yet another global influence identified by Gestalt theory is reflected in the fact that the salience of the illusory figure is influenced by its global simplicity, or symmetry, a manifestation of the Gestalt principle of prägnanz, seen also in the tendency of the soap bubble to assume a globally regular spherical form. Although none of these factors are strictly required for the illusion to succeed, each one adds its own contribution in analog fashion to the salience of the final experience.
It seems therefore that individual aspects of Gestalt visual illusions can be identified and modeled in isolation easily enough, but only by ignoring the larger holistic field-like aspects of Gestalt theory in general. It is hard to imagine how the neural network models proposed to account for collinear completion could be extended to account for the properties of the closure, symmetry, and prägnanz of the figure as a whole, because those are global properties which are simply not conducive to detection or completion by localized receptive field processes. The kind of emergence seen in the soap bubble is also hard to account for in terms of neural network architectures, due to the slow transmission across the chemical synapse, which would limit the speed with which a massively parallel system of neurons can reach equilibrium, especially when the feedback loop involves more than a few synaptic junctions. I propose that the problem is not just a question of finding the right neural network architecture to account for these global phenomena, but that the concept of the spatial receptive field which lies at the core of neural network theory is in principle insufficient to account for these holistic global aspects of perception.
An alternative paradigm of neurocomputation has been proposed in the Temporal Correlation hypothesis (Singer & Gray 1995, Singer 1999), which appears more consistent with the global field-like aspects of perception identified by Gestalt theory. Singer & Gray (1995) propose that synchrony between sets of spiking neurons may represent another channel of information communicated from cell to cell. They propose for example that the global connectivity of a perceived object might be mediated by a common identification signal passed from cell to cell within the connected region, so that all of the cells within that region fire in synchrony with each other. Different groups of active cells in different connected regions would therefore be distinguishable not only by differing activation levels, but by distinct patterns of synchrony within each connected group of cells. There are a number of aspects of this proposal which are promising as an account of the holistic aspects of Gestalt theory. In the first place it suggests a field-like propagation of neural information across regions of neural tissue similar to the diffusion of brightness signal proposed by Grossberg & Todoroviçz (1988) to account for the filling-in of perceived brightness in illusory figures like the Kanizsa triangle. Unlike that model however the neural synchrony paradigm allows multiple dimensions of information encoding in the same neural signal, because different groups of neurons can fire in synchrony within each group, but with a distinct synchrony for each individual group. There are however certain limitations in the temporal correlation paradigm, at least as described by Singer & Gray. In the first place the theory leaves unspecified how the synchrony code itself is generated. If that synchrony is generated in an arbitrary manner, by some kind of random process, then that code would be intrinsically meaningless, devoid of any specific information about the structure of the perceived object that it represents. Although the temporal correlation hypothesis might account for the labeling of connected objects in a scene, it is hard to imagine how this paradigm would account for the kind of completion observed in Gestalt illusory phenomena, where perceptual completion occurs between isolated features which are not explicitly connected, based on their global configuration.
Elsewhere I have proposed a minor but significant extension to the Temporal Correlation hypothesis, in the Harmonic Resonance Theory (Lehar 1994a, 1994b, 1999, 2002). I propose that the synchrony which emerges from a region of connected cells is not arbitrary, but global in nature, like the standing wave resonance that emerges within a resonant cavity or resonating system. Standing waves are by their very nature a global phenomenon, whose characteristics are determined not so much by the local properties of the resonating medium, but by the global configuration of the system as a whole. In fact a system as described by Singer & Gray would naturally tend to generate standing wave patterns within each connected region, based only on the assumption that waves of synchrony within a connected region are propagated freely within that region, but not outside of it. Unless the energy of those waves is actively absorbed, or baffled at the boundaries of the region, they would tend to be reflected back inward towards the interior. Constructive and destructive interference between waves reflecting back and forth within a connected region would automatically result in a pattern of standing waves, like the standing waves that emerge from a resonant cavity in the presence of white noise stimulation. As in the case of a resonant cavity, the frequency and waveform of the resulting standing wave would reflect global aspects of the configuration of the resonating system as a whole. For example larger cavities generate standing waves of longer wavelength and lower frequency than do smaller cavities. There is also a relationship between the shape of the cavity and the waveform of the resultant resonance. A simple shape, like a long thin line, results in simple linear resonances like those in flutes and trumpets, whereas more complex shapes lead to more complex waveforms like those that form in the body of a guitar or violin, with characteristic patterns of higher harmonics. With this minor modification of the Temporal Correlation hypothesis, the synchrony code is no longer arbitrary, but its frequency and waveform reflect certain aspects of the global configuration of the connected feature that they represent. Since a standing wave has a defined spatial structure, this opens the possibility for the kind of structural completion observed in Gestalt illusory phenomena not only within connected regions, but also in the spaces between disconnected features if they are in the right global configuration. For example the three pac-man features of the Kanizsa stimulus mark off a triangular space from the background, whose symmetry, closure, and prägnanz promote the emergence of a triangular standing wave pattern in the neural substrate, by constructive interference between waves of synchronous oscillation reflecting back and forth within that triangular "cavity". This is the kind of holistic perceptual process suggested by the Gestalt illusions.
I propose therefore that the synchrony observed between remote cortical regions is not a signal in its own right communicated between cells to uniquely identify or label connected regions, but rather it is a manifestation of a larger standing wave pattern that spans the cortical region in question, and that the structure of that standing wave pattern in turn encodes certain aspects of the structure of the perceived object or grouping percept. I propose further that the spatial standing wave in the brain serves a function that is normally ascribed to spatial receptive fields in neural network models, i.e. the standing wave serves both for the recognition of characteristic global patterns in the stimulus, and for perceptual completion of the missing portions of those patterns as observed in Gestalt illusions (Lehar 1994a, 1994b, 1999, 2002). I will show that the standing wave offers a much more adaptive and flexible mechanism for encoding spatial structure than the spatial receptive field of the neural network paradigm.
A mechanical system such as a musical instrument that makes use of harmonic resonance as it's principle of operation must have the appropriate physical properties to sustain and control that resonance. But the resonance itself is not a mechanism, or part of the machine, but rather it is a dynamic property of physical matter which is exploited by the machine. There are certain common principles behind resonance and standing wave phenomena in systems as diverse as acoustical resonances in hollow cavities, vibrations in solid objects, laser and maser phenomena, electromagnetic oscillations in electronic circuits, and even chemical harmonic resonances known as reaction diffusion systems. For example all of these systems exhibit a tendency to oscillate at a fundamental frequency, and at its higher harmonics, which occur at integer multiples of the fundamental; the mathematical relationship between the frequency and the wavelength of a standing wave is the same in all these systems, and the phenomena of constructive and destructive interference, all manifest themselves in similar form in all of these diverse resonating systems. The principles of harmonic resonance therefore represent a general organizational principle of physical matter that transcends the details of any particular implementation of it. The harmonic resonance theory presented here is not a specific neurophysiological hypothesis, but more of a paradigm, i.e. a proposed general principle of neural computation and representation that could potentially manifest itself in a number of alternative physical forms in the brain. The principal evidence presented here in support of the harmonic resonance theory is perceptual rather than neurophysiological, which leaves open the exact physical mechanism by which the resonance might actually be mediated in the brain. Specifically, the focus will be on an aspect of illusory contour formation or perceptual grouping which has been very difficult to account for in neural network terms. That is the phenomenon of illusory vertex completion, as seen for example at the corners of the camo triangle, where the illusory sides of that figure are observed to meet at a sharp point or vertex. Illusory vertex completion is far more complex than the collinear completion seen along the sides of the camo and the Kanizsa triangles, because there are many different ways in which illusory edges can meet at a vertex to define a variety of different vertex types, such as "T", "V", "Y" and "X" vertices, among others. And yet the principle behind illusory vertex completion seems to be essentially similar to that behind collinear completion. Therefore a complete model of illusory contours and illusory grouping phenomena would have to account for all of these diverse phenomena by way of a single general principle. I will show with a number of illusory grouping examples that there is in fact an underlying pattern in these various completion phenomena, and that pattern is suggestive of a harmonic resonance explanation in the form of a more specific Directional Harmonic Theory presented below. This model avoids a combinatorial problem inherent in an equivalent neural network solution to the problem, thereby demonstrating the power and adaptiveness of harmonic resonance as a principle of representation in the brain. Finally, harmonic resonance offers a computational principle that exhibits the holistic global aspects of perception identified by Gestalt theory, not as specialized mechanisms or architectures contrived to achieve those properties, but as natural properties of the resonance itself. I propose therefore that harmonic resonance is the long-sought and elusive computational principle behind the holistic global aspects of perception identified by Gestalt theory. The evidence for this hypothesis is somewhat tenuous, appearing as a set of subtle and complex artifacts in various perceptual grouping phenomena, i.e. the evidence by itself is suggestive rather than conclusive. The real appeal of the Harmonic Resonance Theory however is in the broader context because it offers an escape from some of the fundamental limitations inherent in the neural network paradigm. The principal value of the specific predictions of the Directional Harmonic Theory is that they illustrate with specific examples exactly how a resonance model can be formulated to perform specific perceptual computations, which would otherwise require an improbable array of spatial receptive fields in an equivalent neural network model.
Since the evidence on which the present model is founded is perceptual rather than neurophysiological, a perceptual modeling approach will be presented, as opposed to a neural modeling approach. In other words I propose to model the subjective experience of vision directly, in the subjective variables of perceived color, brightness, and form, rather than in terms of neurophysiological variables such as neural spiking frequency or electrical activations. The output of the perceptual model can therefore be matched directly to psychophysical data, as well as to the subjective experience of visual consciousness.
Consider for example the experience of the Kanizsa figure. There is considerable debate as to which aspects of this illusory phenomenon are explicitly represented in the brain and which are encoded in some kind of abbreviated or compressed code. Some have argued that the illusory surface brightness observed to pervade the illusory figure is explicitly encoded with a point-by-point brightness mapping in the brain (Grossberg & Todoroviçz 1988). Others claim that it is only the edges in the image, both real and illusory, that receive explicit encoding, while still others deny that the illusory contours are explicitly encoded at all in the brain (Dennett 1991, 1992, O'Regan 1992, Pessoa et al. 1998). The required output of a neural model of any particular perceptual phenomenon therefore depends on one's prior assumptions on the representational issue. The properties of the subjective experience of the illusion on the other hand are clearly evident by inspection. For the subjective experience of the Kanizsa figure shown in figure 1 B is of a spatial image composed of colored regions, and therefore the output of the perceptual model should also be a spatial image composed of colored regions. The illusory brightness of the Kanizsa figure is observed to pervade the entire surface of the illusory form, with a uniform white percept that is perceived to be brighter than the white background against which it appears. Whatever the neurophysiological basis for this subjective experience therefore, the objective of the perceptual model is to produce an output image that is equal in information content to the subjective experience of the Kanizsa figure. For example in response to an input stimulus as shown in figure 1 B, the perceptual model should produce an output image as shown in figure 1 C. The perceptual model therefore replicates the computational transformation of perception independent of any particular neurophysiological assumptions.
The subjective experience of visual perception encodes more explicit spatial information than can be expressed in a single spatial image. For example the camo triangle shown in figure 1 A exhibits a linear contour around the perimeter of the illusory figure which has no corresponding perceptual brightness component. This illusion demonstrates that perception is capable of presenting spatial structure in visual experience independent of any particular perceptual modality such as perceived brightness or color. Michotte et al. (1964) refer to such modality-independent perceptual experiences as amodal percepts. The Kanizsa figure also incorporates amodal perceptual entities. For example the pac-man features at the corners of the Kanizsa figure are not experienced as segmented or partial circles, but as complete circular discs that complete amodally behind the occluding foreground triangle. A complete perceptual model of the Kanizsa figure would have to include this amodal component of the experience as well as the modal or visible surface percept. However although the amodal percept has no corresponding surface brightness component, it is nevertheless experienced as a vivid spatial structure, and the spatial reality of this perceived structure can be demonstrated by the fact that subjects can easily identify and localize the amodal contour to a high spatial resolution, and indicate its exact spatial path with a pencil. The information content of the amodal percept can therefore be represented as another spatial image, as suggested in figure 1 D, whose visible or explicit contours represent the amodal component of the experience of the Kanizsa figure in figure 1 B. The modal and amodal images in figure 1 C and D together encode the information content apparent in the subjective experience of the Kanizsa stimulus in figure 1 B expressed in objective quantitative terms. The objective of the perceptual model therefore in response to a Kanizsa stimulus as in figure 1 B is to produce an explicit output in the form of the modal and amodal image pair of figure 1 C and D.
The amodal contour image functions something like a line drawing of a scene, whose dark lines separate regions of different brightness in the scene, although the contours in the amodal image are independent of the original contrast polarity of the edge, i.e. the amodal contour is the same whether it corresponds to a dark/ light or a light/dark edge in the stimulus. This two-level description of the subjective experience of perception offers a convenient way to factor the boundary-like processes evident in perception, such as the formation of the illusory contour by collinearity, from the surface-like processes such as the filling-in of the illusory surface brightness within the perimeter of the illusory figure (Grossberg & Todoroviçz 1988). Since illusory contours are sometimes observed to form between edges of opposite contrast polarity, this suggests that the process of illusory contour formation occurs in a representation that is independent of direction of contrast, as suggested in figure 1 D. But the illusory brightness percept in the Kanizsa triangle also suggests that the filling-in process, which must take place in the surface brightness representation, is influenced or channeled by the linear boundaries of the amodal contour representation, as suggested by Grossberg & Todoroviçz (1988). If this theory is correct, then the amodal linear contour of the camo triangle, and the modal contour between regions of different surface brightness in the Kanizsa triangle represent different manifestations of the same underlying amodal contour, the only difference between these two perceptual phenomena being that in the Kanizsa figure the amodal contour is rendered modal, or explicitly visible by the brightness percept that it promotes in the brightness image.
The essential similarity between modal and amodal contours is demonstrated by the fact that an amodal contour can often be transformed into a modal one simply by supplying a contrast across the contour in the stimulus. Consider the dot triangle depicted in figure 2 A. This stimulus is perceived as a "triangle of dots", with a perceived triangular contour joining the three dots with straight line segments that meet at its vertices. This amodal grouping contour can be transformed into a modal brightness percept by the addition of three "v" features as shown in figure 2 B. The resulting modal percept highlights the otherwise amodal contour with an actual perceived brightness contrast along the entire edge, and that edge is perceived to bound a region of illusory brightness that pervades the entire surface of the illusory triangle. Figure 2 C depicts a shifted line-grid stimulus whose upper transition produces an illusory contour along the shear line of the figure which is almost entirely amodal. However this figure too can be transformed into a modal surface brightness percept by arranging for a different line density on either side of the shear line, as shown in the lower transition of the same figure. The amodal camo triangle of figure 1 A can also be transformed into a modal surface brightness percept by arranging for a different texture density between figure and ground, as shown in figure 2 D. In the discussion that follows therefore, it will be assumed that the amodal grouping contour is a real and explicit perceptual entity constructed by perceptual processes, and that the modal surface brightness contour is a visible or modal manifestation of the same underlying invisible or amodal linear contour. Furthermore, I propose that there is no substantive distinction between illusory contours and perceptual grouping phenomena, and that in fact a perceptual grouping is identically equal to an amodally perceived structure that links the grouped items.
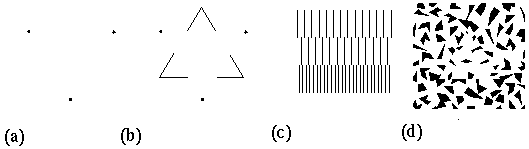
(a) The amodal dot triangle. (b) The modal dot triangle. (c) The shifted line-grid illusion, amodal at the upper shear line, and modal at the lower shear line. (d) The modal camo triangle.
There are several distinct characteristics observed in different types of illusory contours, that suggest distinct computational principles underlying illusory contour formation. These different types of contours can be classified as collinear, orthogonal, and vertex type contours. The collinear contour is the simplest form, as observed in both the camo triangle and the Kanizsa figure shown in figure 1 A and B respectively. This phenomenon demonstrates the perceptual tendency of the illusory contour to form parallel to oriented line segments in the stimulus. Figure 3 A depicts the Ehrenstein illusion, which demonstrates the second type of contour formation principle. In this figure the contour is observed to form orthogonal to the oriented line segments in the stimulus. The same principle of orthogonal completion is also evident in the shifted line-grid stimulus of figure 2 C. The third principle of illusory contour formation through sharp corners or vertices is demonstrated at the corners of the amodal and modal dot-triangles shown in figure 2 A and B. This is the most complex and variable of the three principles of illusory contour formation, for although in this case the contour is composed of two illusory contours that meet at an acute angled vertex, other examples (which will be presented below) reveal illusory vertices composed of the intersection of three, four, or more illusory contours that meet at a point.
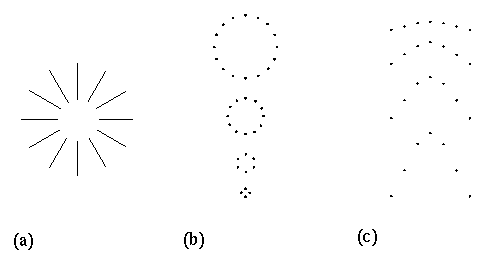
(a) The Ehrenstein illusion. (b) A circle of dots becomes, with increased curvature, a polygon of dots with an illusory vertex at each dot location. (d) A line of dots also becomes kinked perceptually beyond a certain limiting curvature.
Although these different forms of illusory contour formation exhibit distinct characteristics, there is compelling evidence that they are nevertheless different manifestations of the same underlying mechanism. For example Kanizsa (1987) observes that the collinear grouping percept due to a circle of dots gives way to a polygonal percept when the number of dots in the circle is reduced, as shown in figure 3 B. In other words the collinear grouping contour passing through each dot gives way to a vertex grouping percept, as if the collinear contour kinks like a drinking straw that is bent beyond its elastic limit. The same phenomenon can be demonstrated with a line of dots as shown in figure 3 C. This phenomenon appears to be related to a similar abrupt transition observed in the perception of curvature (Wilson & Richards 1989).
An even more complex repertoire of perceptual interaction is observed in dot grouping percepts as shown in figure 4. Figure 4 A shows a pattern of dots that are grouped in pairs, i.e. an illusory grouping line is observed to connect the two dots of the pair as suggested schematically by the gray shading in the magnified depiction on the right of the figure. In other words each dot projects a single illusory contour extending out in one direction only. A different pattern is observed in figure 4 B which shows a collinear grouping of dots in columns, each dot being connected by an illusory grouping contour that extends out from that dot in opposite directions, as shown schematically to the right of the figure. Figure 4 C shows a hexagonal grouping pattern in which each dot defines the center of a three-way vertex, as suggested schematically to the right in the figure. Finally figure 4 D depicts a grid-like percept in which each dot defines the center of a four-way vertex, as suggested schematically to the right in the figure.

Dot grouping phenomena. Amodal illusory contour formation through vertices composed of (a) one, (b) two, (c) three, and (d) four intersecting illusory contours, as suggested schematically to the right, where the gray lines represent the perceived contours in the figures to the left.
What is interesting in these perceptual phenomena is not so much the perceived grouping that occurs between neighboring dots, i.e. a grouping by the Gestalt law of proximity, but there is a more subtle and complex inhibitory effect whereby a nearer grouping is seen to suppress a more distant grouping. For example the horizontal separation between columns of dots in figure 4 B is the same as that in the grid pattern of figure 4 D. But the closer vertical spacing within each column in figure 4 B appears to suppress the horizontal grouping between those dots. Similarly, the vertical and horizontal grid grouping percept of figure 4 D appears to suppress an equally valid diagonal dot grouping, because each dot is located at the intersection of two diagonal rows of dots as well as on vertical and horizontal columns and rows of dots. But since the vertical and horizontal grouping has a closer spacing than the diagonal grouping, the diagonal grouping percept is entirely suppressed in this dot pattern. Similarly the hexagonal grouping percept shown in figure 4 C suppresses an equally present vertical and horizontal grouping percept, because each dot is located on the intersection of a vertical column and a horizontal row of dots in the stimulus, although this pattern is not apparent in the grouping percept. These complex spatial interactions between different grouping patterns offer a detailed manifestation of the specific computational interactions in perception, that goes well beyond the simplistic collinear and orthogonal grouping phenomena which are the usual focus of psychophysical studies. It is this secondary subtle pattern of inhibitory effects which provide the principal evidence for the Directional Harmonic Model.
A similar parametric variation between different perceptual grouping patterns can be seen in patterns composed of line segments as shown in figure 5. For example the lines in figure 5 A group into columns by collinearity, i.e. the illusory contour forms parallel to the inducing line segments, as suggested schematically to the right in figure 5 A. With a closer horizontal spacing however the percept becomes one of an orthogonal grouping, as shown in figure 5 B, and as suggested schematically to the right in the figure. This orthogonal grouping is similar in principle to the Ehrenstein illusion of figure 5 A, and the shifted line-grid stimulus of figure 2 C. Again it is interesting that the closer horizontal spacing seems to suppress the alternative vertical grouping percept, and vice-versa. A third diagonal grouping percept can also be obtained with the proper arrangement of line segments, as shown in figure 5 C, and as suggested schematically to the right in the figure. This percept is considerably less salient than the collinear and orthogonal grouping percepts, and is complicated by the fact that it is not entirely clear whether the grouping lines connect adjacent line endings directly, as suggested schematically to the right in the figure, or whether diagonal rows of line segments form intersecting diagonal "streets", i.e. with longer grouping lines that extend from the top of one line segment to the top of the next and on to the top of the next, rather than from the top of one line ending to the bottom of the next. This illusion is further complicated by the fact that the percept is somewhat bistable or rivalrous between a percept of parallel diagonal streets from lower left to upper right, in competition with diagonal streets from upper left to lower right. However there is clearly a diagonal component to the percept that is clearly distinct from the collinear and orthogonal percepts of figure 5 A and B, and this percept appears to involve a completion by illusory vertex formation with a "Y" vertex at the tip of each line segment.
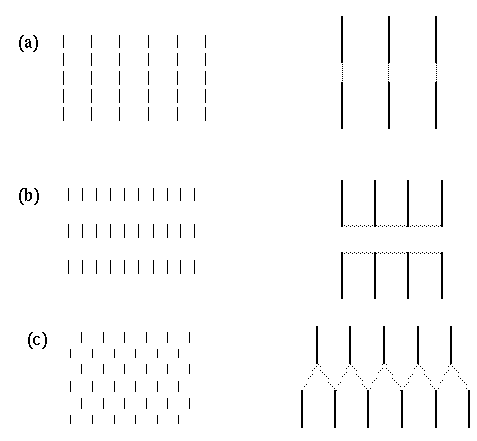
Line segment phenomena. Amodal illusory contour formation through vertices composed of (a) one, (b) two, (c) three, and (d) four intersecting illusory contours, as suggested schematically to the right, where the gray lines represent the perceived contours in the figures to the left.
The grouping percepts in figures 4 and 5 are primarily of an amodal nature, although there is perhaps also a faint modal or surface brightness component to them. But the principal focus of the present analysis is on the pattern of amodal grouping observed in these stimuli, regardless of whether or not those amodal contours also promote a corresponding surface brightness percept. The shaded grouping lines shown schematically to the right in figures 5 and 6 therefore represent the amodal component of the grouping percept, as was the case in figure 1 D, and therefore these patterns of gray lines represent the amodal output image that should be produced by an adequate computational model of these perceptual grouping phenomena.
The central pattern formation mechanism in neural network theory is the spatial receptive field, whose spatial pattern of excitatory and inhibitory synapses determines the spatial pattern to which a particular neuron responds. But the spatial receptive field is no different in principle from a template theory, a concept whose limitations are well known. A template is a spatial map of the pattern to be matched, which is inherently intolerant to any variation in the stimulus pattern. For example a mismatch will be recorded if the pattern is presented at a different location, orientation, or spatial scale than that encoded in the template. Therefore the only way to achieve invariance in a neural network or template model is to provide templates for every possible variation of the pattern to be matched, for example for every orientation, location, and spatial scale. But full invariance requires also templates for every combination of variations, for example a different template for every rotation of the pattern at every possible scale, all replicated at every spatial location. This leads to a combinatorial explosion in the required number of templates for invariant recognition even of simple forms such as squares, rectangles, and triangles.
The solution to the problem of invariance commonly proposed in neural modeling is a feature based approach, i.e. to break the pattern into its component features, and detect those local features independently of the whole (Selfridge 1959, Marr 1982, Biederman 1987). Very simple features such as oriented edges, bars, or corners, are sufficiently elemental that it would not be prohibitive to provide templates for them at every location and orientation across the visual field. For example a square might be defined by the presence of four corners, each of which might be detected by a local corner detector applied at every location throughout a local region of the image. The enumerative listing of four corner features would be the same for squares of different rotations, translations, and scales, and therefore the feature list as a representation is invariant to rotation, translation, and scale.
Despite the current popularity of the feature detector concept in neural network models, the fundamental limitations of this approach to perception were pointed out decades ago by Gestalt theory. In the first place, local features cannot be reliably identified in the absence of the global context. This is particularly clear in exemplary cases like the camo triangle, although it is equally true, while less obvious, in the case of natural imagery. For example a corner detector in computer simulations will typically generate countless corner responses in a natural scene, only a small fraction of which would be identified as legitimate corner features in the global context. Another problem with the feature based approach is that in the tally of detected features, it is impossible to determine reliably which features belong to which objects. Whatever local region is selected for the tally of detected features, might just as well include features from several different objects to confound the feature list, and conversely, the object centered on that region might extend out beyond the region, and thereby lose critical features from its feature list. A feature based system would also be easily misled by spatial occlusions, which occur commonly in visual scenes, but appear to pose no serious problem to visual recognition.
Finally, the feature based theory has a serious problem with the reification, or perceptual filling-in observed in Gestalt illusions like the Camo and the Kanizsa figures. The principle by which the feature based theory escapes the combinatorial problem inherent in the template theory is by way of a progressive abstraction or information compression from lower to higher levels in the visual hierarchy. For example many different configurations of corners can trigger a single triangle detector node, so that different nodes are not required to represent every possible variation of a triangle individually. In other words there is a many-to-one relation between the many possible stimulus configurations and the invariant recognition response that they all stimulate. However a top-down feedback from such an invariant representation suggests a one-to-many relation which would necessarily stimulate all of the possible stimulus configurations which could have given rise to that invariant response. For example if the corners of the camo triangle trigger the same acute-angled- vertex detector regardless of the orientation that the vertex is presented, a top-down feedback from that invariant vertex detector would generate vertex percepts at all orientations simultaneously, because the orientation information is not encoded in the rotation-invariant code. This is in contrast to the observed properties of illusory figures like the camo or the Kanizsa triangle in which the illusory form appears at a precise location, orientation, and spatial scale, and in the case of the Kanizsa triangle, with a precise contrast against the background. What is required to account for these Gestalt illusions is a kind of top-down completion that makes use of the higher level recognition of the object to determine its precise configuration in the context of the given stimulus, i.e. something like an elastic template which is somehow warped or distorted in order to match the specific configuration of the given stimulus. This kind of elastic flexibility in top-down completion is in principle beyond the capacity of the rigid template mechanism inherent in neural network theory.
An alternative trend in neural network theory has been to propose dynamic neural network (DNN) models, as opposed to the "grandmother cell" or the hierarchical feature detector concept of visual representation. In a dynamic neural network model, it is not so much individual cells whose activation encodes the recognition of features in the stimulus, but rather it is dynamic patterns of activation in the neural substrate which reflect the perceived structure of the scene. On the face of it, this concept seems particularly promising to account for the field-like aspects of perception identified by Gestalt theory, such as the phenomena of collinear contour completion, and surface brightness filling-in. However this promise is illusory, because in fact the DNN concept of neural processing still depends on the spatial receptive field as its central principle of spatial representation, and therefore this paradigm does not escape the combinatorial problem inherent in neural network approach to invariance.
Consider a DNN model composed of a two-dimensional layer of identical neurons connected to each other within the layer by way of center-surround receptive fields, i.e. with short-range excitatory, and long-range inhibitory feedback connections as suggested in figure 6 A. Each neuron in the layer has its own input channel, so the pattern of input defines an input layer of the same dimensions as the feedback layer, as suggested in figure 6 A. If the input image is initialized with a random noise pattern as shown in figure 6 B, the recurrent feedback within the DNN layer will result in an equilibrium state characterized by active regions separated by regions of inactivity, in an irregular, but approximately periodic pattern with a certain average spacing between active regions. Figure 6 B depicts the results of a computer simulation of this effect, produced by spatial convolution of the random noise input with the convolution filter, or receptive field depicted to the left in figure 6 B. The dark region at the center of the filter represents positive filter values, the white annulus around it depicts negative values, and the neutral gray shade at the edges depict zero values in the filter. This particular filter was defined mathematically as a difference-of-Gaussians, i.e. a larger Gaussian subtracted from a smaller one. Different random input images generate different equilibrium patterns, although all of those patterns are characterized by an approximately periodic pattern with a certain average spacing between active regions. This demonstrates the power of the DNN concept, because instead of defining a template for a single stored pattern, the DNN encodes essentially an infinite variety of different patterns, all of which share a common characteristic spatial quality. The kind of structured field-like interaction within the DNN layer is suggestive of the kind of field-like forces in Gestalt theory, for example those that lead to perceptual grouping of nearby elements, or grouping by proximity. For example if the input image consists of clusters of dots, as shown in figure 6 C, each cluster stimulates the emergence of a field-like patch of activation in the DNN layer encompassing that cluster, as seen for the two dot clusters at the left in figure 6 C. This DNN model might therefore serve as a model of perceptual grouping by proximity of clusters of dots, with each perceived group or cluster being marked by a patch of activation in the feedback layer. However the characteristic behavior of this network, i.e. the average size of active regions and the average spacing between them, must be explicitly encoded in the pattern of the receptive fields of the model. One of the most perplexing aspects of perceptual grouping by proximity is that it appears to be not a function of absolute scale, i.e. with grouping occurring only between elements found within a certain separation in visual angle, but rather grouping occurs by some kind of relative proximity measure, which allows perceptual grouping of both small and large clusters of dots through a large range of spatial scales. This scale invariance is not a natural property of the DNN paradigm. For example the cluster of dots at the upper-right in figure 6 C fails to form a perceptual grouping response in the DNN layer because these dots are too far apart for the receptive field size used in this simulation. In order to account for this kind of grouping, the DNN model would have to be equipped with many different receptive fields through a large range of spatial scales, all of which would have to be replicated at every spatial location throughout the layer. Furthermore, some kind of cooperative or competitive mechanism would also have to be provided to define the interactions between different spatial scales, although it is not at all clear how those interactions would have to be organized.

(a) A Dynamic Neural Network (DNN) model consisting of a two-dimensional array of nodes in the feedback layer, each of which is connected to other nodes in the feedback layer by way of short-range excitatory (dark shaded region) and longer-range inhibitory (white annular region) synaptic connections. Each node in the feedback layer also receives input from a corresponding location in the input layer. (b) Computer simulation of a DNN model as described above, showing actual receptive field profile used in the simulation. When stimulated with a random noise input, this kind of feedback results in quasi-periodic regions of activation (darker blobs) in the feedback layer, separated by regions of less activation (light regions) with a periodicity that is determined by the spatial properties of the receptive field used. (c) Computer simulation of a DNN model given an input signal in the form of clusters of dots in the input image. When the spacing between dots in the cluster matches the size of the central excitatory region of the feedback receptive field, the cluster produces a region of activation in the feedback layer, representing a Gestalt grouping by proximity. When the spacing of dots is too wide however, as in the cluster to the upper right, no proximity grouping occurs, because each dot falls within the inhibitory region of the receptive fields of the other dots. This demonstrates that a grouping by proximity in a DNN model of this sort is sensitive to the spatial scale of the receptive field used.
The phenomenon of collinear illusory contour formation suggests a more structured or directional pattern of interaction than in grouping by proximity, with neural activation propagating anisotropically in a direction parallel and collinear to stimulus edges. This can also be implemented in a DNN model by providing anisotropic or directional receptive fields in the feedback layer. For example a receptive field can be defined which is excitatory in the horizontal direction and inhibitory, in the vertical direction, as shown schematically in figure 7 A. Given a random noise input signal, this kind of system produces at equilibrium a quasi-periodic pattern of horizontal lines of activation as shown in the computer simulations of figure 7 B, although again the exact pattern would vary with different random input patterns. However providing the receptive field with an orientation opens a new dimension of variability, because perceptually, collinear completion can occur at any orientation. Therefore a complete DNN model of collinear completion would have to be equipped with a full set of anisotropic receptive fields, one for every possible orientation replicated at every spatial location in the model. This is shown in the computer simulations of figure 7 C, which shows four different layers of cells representing edges at four different orientations. Each of these layers is equipped with anisotropic feedback receptive fields oriented parallel to the orientation represented by that plane, as shown to the left in figure 7 C, in order to perform collinear completion in each plane only in the direction specific to that plane. These particular filters were defined mathematically by a Gaussian function in the oriented direction and a difference-of-Gaussians function in the orthogonal direction.
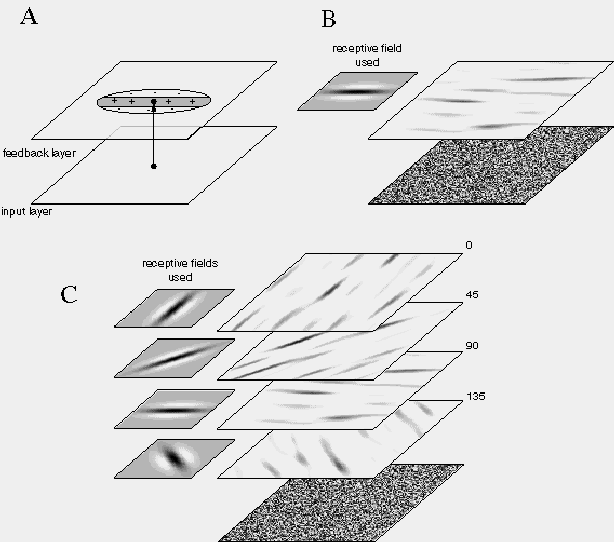
(a) A Dynamic Neural Network (DNN) model to perform collinear perceptual grouping by way of an anisotropic or directional receptive field profile with excitatory connections in one direction (horizontal) and inhibitory connections in the other (vertical). (b) A computer simulation of a horizontal collinear grouping in response to a random noise input, showing the actual receptive field profile used in the simulation. (c) A computer simulation of a similar DNN model, this time equipped with four different feedback receptive field profiles, each one tuned to perform collinear completion in one of four different orientations.
Collinear contour formation is influenced by the orientation of the edges in the stimulus, the strongest completion occurring between edges which are both parallel in orientation and spatially aligned. This suggests that the input to the feedback layer should be provided by oriented edge detector cells, equipped with specialized receptive fields tuned to detect edges of a particular orientation in the manner of cortical simple cells suggested by Hubel & Wiesel. Each oriented layer of the DNN shown in figure 7 C would therefore receive input only from edge detectors tuned to the appropriate orientation for that layer. This model can now replicate the directed propagation of neural activation between horizontal collinear edges as seen along the base of the Camo and Kanizsa triangles. In simplified form, this is the general principle behind several neural network models of collinear illusory contour formation, including Grossberg & Mingolla (1985, 1987), Walters(1987), and Zucker et al. (1989).
At first sight this concept might seem adequate as a general principle of collinear contour formation, although presented here in its simplest, most general form. However the general principles embodied in this model clearly reveal the limitations of a neural network approach to this problem. The DNN attempts to escape the combinatorial problem inherent in the template theory concept of neural representation by replacing it with the concept of dynamic fields of activation across the neural tissue. However the dynamic spatial properties of those fields are still determined by hard-wired neural receptive fields. Every different type of spatial behavior required of the network requires another specialized set of receptive fields tuned to achieve that behavior. Furthermore, some kind of cooperative or competitive interactions must also be defined between those sets of receptive fields in order to select between alternative behaviors of the system. For example a collinear completion model experiences a conflict at every corner or vertex in the image, where two or more orientations are detected at the same location, resulting in multiple oriented responses active at those locations. However it is not entirely clear what the appropriate interaction should be between conflicting oriented edge responses. Grossberg & Mingolla (1985, 1987) propose a specialized kind of competition tuned to promote orthogonal oriented edges at an abrupt line ending, in order to account for the phenomenon of orthogonal completion, as seen for example in the Ehrenstein illusion. However whatever the mechanism contrived to account for orthogonal completion of this form will be difficult to generalize to account for the other types of completion such as vertex completion of a variety of different forms. For to do this, the model would have to be equipped with a different set of spatial templates for every possible pattern of vertices such as T, V, and L vertices etc., as suggested by Grossberg & Mingolla (1985), and each of those different vertex templates would have to be provided at every location, at every orientation, and every spatial scale. Furthermore, cooperative or competitive interactions would also have to be defined between every combination of these different completion types in order to select the right kind of completion in cases of ambiguity or conflict. More generally, the solution of the DNN paradigm to the combinatorial problem in neural networks is to provide templates for every possible permutation and combination of every pattern which it is capable of completing. This is clearly not a promising general principle of representation in the brain.
The dynamic neural network is not really a single mechanism, but a set of specialized mechanisms, one for each distinct type of behavior required of the system. What is required for a more plausible model of illusory contour formation is a single mechanism or computational principle to account for all of the diverse completion phenomena, in order to escape the combinatorial problem inherent in neural network approach. In other words a plausible model of perceptual completion should not involve a combinatorial array of explicit vertex detectors at every rotation, translation, and scale, but a more general dynamic mechanism with a whole set of distinct dynamic modes of behavior corresponding to all those different vertex types. Harmonic resonance offers a computational principle with the required representational flexibility and invariance.
The Harmonic Resonance theory (Lehar 1994a, 1994b, 1999, 2002) offers a computational paradigm with the holistic global properties identified by Gestalt theory. The most remarkable property of harmonic resonance is the sheer number of different unique patterns that can be obtained in even the simplest resonating system. A pioneering study of more complex standing wave patterns was presented by Chladni (1787) who demonstrated the resonant patterns produced by a vibrating steel plate. The technique introduced by Chladni was to sprinkle sand on top of the plate, and then to set the plate into vibration by bowing with a violin bow. The vibration of the plate causes the sand to dance about randomly except at the nodes of vibration where the sand accumulates, thereby revealing the spatial pattern of nodes. This technique was refined by Waller (1961) using a piece of dry ice pressed against the plate, where the escaping gas due to the sublimation of the ice sets the plate into resonance, resulting in a high pitched squeal as the plate vibrates. Figure 8 (adapted from Waller 1961 P. 69) shows some of the patterns that can be obtained by vibrating a square steel plate clamped at its midpoint. The lines in the figure represent the patterns of nodes obtained by vibration at various harmonic modes of the plate, each node forming the boundary between portions of the plate moving in opposite directions, i.e. during the first half-cycle, alternate segments deflect upwards while neighboring segments deflect downwards, and these motions reverse during the second half-cycle of the oscillation. The different patterns seen in Figure 8 can be obtained by touching the plate at a selected point while bowing at the periphery of the plate, which forms a node of oscillation at the damped location, as well as at the clamped center point of the plate. The plate emits an acoustical tone when bowed in this manner, and each of the patterns shown in figure 8 corresponds to a unique temporal frequency, or musical pitch, the lowest tones being produced by the patterns with fewer large segments shown at the upper-left of figure 8, while higher tones are produced by the higher harmonics depicted towards the lower right in the figure. The higher harmonics represent higher energies of vibration, and are achieved by damping closer to the central clamp point, as well as by more vigorous bowing.
Chladni figures for a square steel plate (adapted from Waller 1961) demonstrates the fantastic variety of standing wave patterns that can arise from a simple resonating system. A square steel plate is clamped at its midpoint and sprinkled with sand. It is then set into vibration either by bowing with a violin bow, or by pressing dry ice against it. The resultant standing wave patterns are revealed by the sand, that collects at the nodes of the oscillation where the vibration is minimal.
The utility of standing wave patterns as a representation of spatial form is demonstrated by the fact that nature makes use of a resonance representation in another unrelated aspect of biological function, that of embryological morphogenesis, or the development of spatial structure in the embryo. After the initial cell divisions following fertilization, the embryo develops into an ellipsoid of essentially undifferentiated tissue. Then, at some critical point a periodic banded pattern is seen to emerge as revealed by appropriate staining techniques, shown in figure 9 A. This pattern indicates an alternating pattern of concentration of morphogens, i.e. chemicals that permanently mark the underlying tissue for future development. This pattern is sustained despite the fact that the morphogens are free to diffuse through the embryo. The mechanism behind the emergence of this periodic pattern is a chemical harmonic resonance known as reaction diffusion (Turing 1952, Prigogine & Nicolis 1967, Winfree 1974, Welsh et al. 1983) in which a continuous circular chemical reaction produces periodic patterns of chemical concentration in a manner that is analogous to the periodic patterns of a resonating steel plate. The chemical harmonic resonance in the embryo can thereby define a spatial addressing scheme that identifies local cells in the embryonic tissue as belonging to one or another part of the global pattern in the embryo by way of the relative concentration of certain morphogens. The fact that nature employs a standing wave representation in this other unrelated biological function offers an existence proof that harmonic resonance both can and does serve as a spatial representation in biological systems, and that representation happens to exhibits the same holistic Gestalt properties that have been identified as prominent properties of perception and behavior.
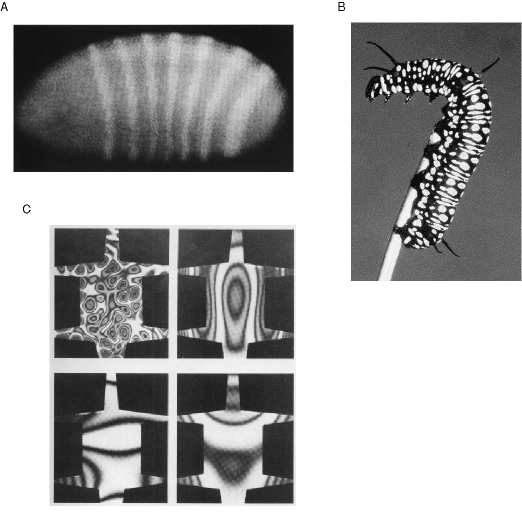
(a) A periodic banded pattern revealed by chemical staining emerges in a developing embryo, due to a chemical harmonic resonance whose standing waves mark the embryonic tissue for future growth. (b) This chemical harmonic resonance has been identified as the mechanism behind the formation of patterns in animal skins, as well as for the periodicity of the vertibrae of vertibrates, the bilateral symmetry of the body plan, as well as the periodicity of the bones in the limbs and fingers. (c) Murray shows the connection between chemical and vibrational standing waves by replicating the patterns of leopard spots and zebra stripes in the standing wave resonances in a vibrating steel sheet cut in the form of an animal skin.
Oscillations and temporal resonances are familiar enough in neural systems and are observed at every scale, from long period circadian rhythms, to the medium period rhythmic movements of limbs, all the way to the very rapid rhythmic spiking of the single cell, or the synchronized spiking of groups of cells. Harmonic resonance is also observed in single-celled organisms like the paramecium in the rhythmic beating of flagella in synchronized travelling waves. Similar waves are observed in multicellular invertebrates, such as the synchronized wave-like swimming movements of the hydra and the jellyfish, whose decentralized nervous systems consist of a distributed network of largely undifferentiated cells. The muscle of the heart provides perhaps the clearest example of synchronized oscillation, for the individual cells of the cardiac muscle are each independent oscillators that pulse at their own rhythm when separated from the rest of the tissue in vitro. However when connected to other cells they synchronize with each other to define a single coupled oscillator. The fact that such unstructured neural architectures can give rise to such structured behavior suggests a level of computational organization below that of the switching and gating functions of the chemical synapse. The idea of oscillations in neural systems is not new. However the proposal advanced here is that nature makes use of such natural resonances not only to define rhythmic patterns in space and time, but also to define static spatial patterns in the form of electrical standing waves, for the purpose that is commonly ascribed to spatial receptive fields. There is plenty of neurophysiological evidence which has accumulated over the last few decades suggestive of harmonic resonances in the brain (Gerard & Libet 1940, Bremer 1953, Eckhorn et al. 1988, Nicolelis et al. 1995, Murthy & Fetz 1992, Sompolinsky et al. 1990, Hashemiyoon & Chapin 1993). However it has been hard to interpret the significance of that evidence in the absence of a paradigmatic framework to suggest what function that resonance might serve in perception. I will show that as a paradigm for defining spatial pattern, the standing wave offers a great deal more flexibility and adaptiveness to local conditions than the alternative receptive field model, and that a single resonating system can replace a whole array of hard-wired receptive fields in a conventional neural model.
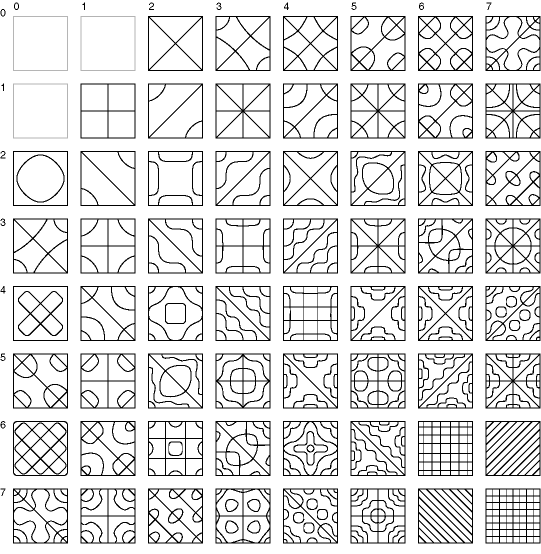
One of the most interesting aspects of harmonic resonance as a representational principle in the brain is that it exhibits certain invariances which are also characteristic of perception (Lehar 1994a, 1994b, 1999, 2002). Figure 10 shows the Chladni figures for a circular steel plate. This system exhibits two kinds of periodicity, a radial periodicity in the form of concentric rings, and a circumferential or directional periodicity in the form of radial lines, and these two types of periodicity appear in a variety of combinations. However due to the circular symmetry of the plate, each of these patterns can actually appear on the plate at any orientation. This is a very powerful feature, because if a standing wave pattern does indeed function as a spatial template in the brain, then any one of these patterns of standing waves corresponds not only to a single template in an equivalent neural network model, but to a whole array of them, i.e. with each pattern replicated at every possible orientation. Given that all of the different patterns in figure 10 are produced by a single mechanism, this one circular plate, and its various standing wave patterns represents the computational equivalent of a whole array of different spatial templates in a neural network model, each one replicated at every possible orientation. It is this invariance feature of a harmonic resonance representation that offers an escape from the combinatorial problem inherent in the neural network paradigm. Furthermore, not only does the circular Chladni plate represent a whole array of equivalent neural receptive fields, but also the cooperative or competitive interactions between them, because the various harmonics of the plate interact with one another in lawful ways, and these interactions make specific predictions about the behavior of a harmonic resonance model in response to certain patterns of input.
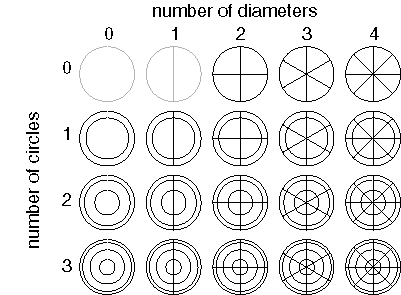
Chladni figures for circular plate, sorted by number of [diameters, circles] in each pattern. These patterns can appear at any orientation on the plate. Each distinct pattern has a unique vibration frequency. The vibration frequency therefore offers a rotation invariant representation of the pattern present on the plate.
The phenomenon of harmonic resonance is immensely complex, involving parallel interactions in all directions simultaneously through a homogeneous continuum in a manner that defies complete mathematical characterization or accurate numerical simulation in all but its simplest aspects. That very complexity however is exactly why harmonic resonance holds such great potential as a principle of computation and representation in the brain. The focus of this paper will be restricted to a single aspect of harmonic resonance, i.e. the tendency for standing waves to form patterns of circumferential, or directional periodicity, like the patterns of radial node lines seen in figure 10, as suggested originally by Lehar (1994a, 1994b). For the dot grouping patterns presented in figure 4 suggest a periodic basis set of different vertex types, expressed in terms of directional periodicity, which are suggestive of these patterns of standing waves. As in the case of a Fourier representation, any pattern of vertices can be represented in a directional harmonic code to arbitrary precision, by the appropriate combinations of harmonic coefficients. However in a physical system, the higher order terms require higher vibrational energies, as is the case for the Chladni figures. A physical harmonic resonance representation would therefore necessarily be band-limited to the lower harmonics, with a cut-off at some highest harmonic of directional periodicity. This low-pass cut-off introduces a certain granularity or quantization in the representation, limiting the complexity of the kind of vertex completion patterns to some finite set of low-order primitives. In fact it is this granularity in the directional harmonic code which accounts for the geometric regularity of the illusory grouping percepts observed in the different dot grouping patterns, as will be shown below.
The dot grouping patterns observed in figure 4 can be explained by a system that promotes local standing wave patterns at every dot location in the feedback layer, in response to the pattern of influence felt from neighboring dots in adjacent regions. Initially, each dot stimulates a point of activation at the corresponding location in the feedback layer, and that activation propagates radially outward by passive diffusion in all directions from each point. The diffusing activation from neighboring points of activation in turn impinges back on the original point from different directions, and the reciprocal exchange of energy back and forth between these active points across the feedback layer promotes the emergence of a pattern of standing waves of directional harmonic resonance at each active point as described below. Although harmonic resonance is a dynamic process that proceeds to equilibrium, a simplified static model of the process is sufficient to account for many of the observed grouping effects. This is analogous to the heat equation which describes the dynamic propagation of heat along a conductor from a localized source. Given a regular rate of heat loss along the conductor, the heat equation can be solved at equilibrium to produce a declining temperature gradient along the conductor with distance from the localized source, as a static model of the equilibrium state of a dynamic process. Similarly, the pattern of activation in the feedback layer of the directional harmonic model due to the presence of stimulus dots is assumed to produce at equilibrium a static gradient of activation, declining outward from each stimulus point with a Gaussian profile, as a static approximation to the equilibrium state of a dynamic diffusion process. The patterns of standing waves of directional periodicity are then computed at each stimulus dot location in response to this static input field from adjacent dots as described below.
For clarity this calculation is divided in two stages, an input stage, and a resonance stage. The input signal at each dot location is a circular signal, somewhat like a trace on the scope of a radar that scans the horizon in a circular sweep, producing peaks in every direction in which other dots are detected from that location. For example figure 11 A shows a pattern of dots around a central dot (circled), and figure 11 B shows the circular input signal Iq at that central dot for every direction q from that dot, expressed in degrees clockwise from the vertical. The neighboring dot in the 12 o'clock direction in figure 11 A produces a peak in the input response at 12 o'clock, or 360 degrees, as shown in figure 11 B, and the other dots produce similar peaks in the corresponding directions. The magnitude of the input signal fades as a Gaussian function of radial distance r between points, due to the passive diffusion, and this fading is modeled by the Gaussian function
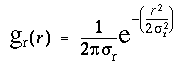
|
(EQ 1) |
where sr is the standard deviation of the radial Gaussian function. This spatial decay explains why the dot at the 9 o'clock direction in figure 11 A produces a smaller peak in the input signal in the 9 o'clock direction in figure 11 B, because of the larger distance to that dot. The larger dashed circle shown in figure 11 A depicts the radius corresponding to two standard deviations (2sr) of the radial Gaussian input function used in these simulations. If the activation due to a dot were confined to a singular point, the input peak due to that dot would actually appear as an impulse function, i.e. a singularity in orientation. But the passive diffusion through the feedback layer would be expected to spread that singular peak somewhat across neighboring directions. In the simulations therefore the input signal Iq was modulated by an angular Gaussian function of the form
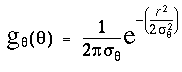
|
(EQ 2) |
i.e. this is the same Gaussian function as used in the radial Gaussian term, except that it operates in the angular dimension, with a standard deviation sq of 2p x .05 or 18 degrees, in order to spread that impulse response into a more manageable peak of finite size, as seen in this plot. The equation for the input signal therefore due to one neighboring dot at a bearing of a degrees from the central dot is given by
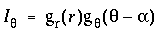
|
(EQ 3) |
(EQ 2)
The input signal is additive in each direction, so the three dots shown in the 3 o'clock direction in figure 11 A together produce a stronger peak in figure 11 B than any one of them would produce by themselves. The three dots near the 6 o'clock direction on the other hand are each in slightly different directions, and therefore they produce three individual input peaks through the 6 o'clock direction as seen in figure 11 B. The full equation therefore for the input signal Iq due to a set of n neighboring dots di i=1...n, at distances ri, and at angular bearings of ai, is given by
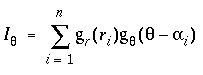
|
(EQ 4) |
Although the input signal is plotted only for the central dot in figure 11 A, a similar input signal is computed at every dot location in the simulations presented below. This circular input signal is then used to compute the circular harmonic resonance response at each dot location, as described below.
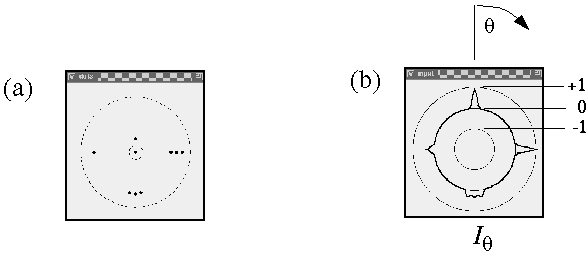
Computer simulation of the circular input signal at a central dot location due to the presence of adjacent dots. (a) A pattern of dots around a central dot (circled). The larger dotted circle indicates a radial distance which is twice the standard deviation of the radial Gaussian term. This pattern of input dots produces (b) a circular input function at the central dot location, showing how each adjacent dot produces a positive peak in the corresponding direction, the magnitude of the peaks being modulated by the distance from the central dot.
Figure 12 A depicts a circular harmonic series of directional periodicity, whose nodes, or stationary points (depicted as radial lines) represent the various edges that meet at the vertex. The first harmonic of directional periodicity exhibits a single node extending outward from the center in one direction. This harmonic corresponds to an end-stop feature, or unilateral vertex, as seen in the dot grouping pattern of figure 4 A. The second harmonic exhibits two nodes separated 180 degrees, which corresponds to a collinear vertex, or collinear grouping percept, as seen in figure 4 B. The third harmonic represents a three-way or "Y" vertex composed of three edges that meet at 120 degrees as seen in figure 4 C, and the fourth harmonic represents a "+" or "X" vertex with edges separated by 90 degrees as seen in figure 4 D. There is also a zeroth harmonic, like the DC term in a Fourier code, which represents the energy across all directional frequencies simultaneously. The zeroth harmonic corresponds to a vertex composed of edges extending in all directions simultaneously, which, in the limit, is essentially equivalent to no edges at all. Figure 12 B plots the amplitude function Aq of each of these harmonics as a pattern of nodes and anti-nodes around the circle from q = 0 to 2p, i.e. the height of the plot represents the amplitude of the vibration as a function of angle through the circle, which is given by
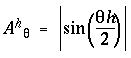
|
(EQ 5) |
for harmonics h = 1 to 4. Actually this figure shows a double plot, with upper and lower traces showing the positive and negative of the amplitude, representing a vibration alternately upward and downward from zero, like the pattern of vibration of a guitar string, to emphasize that the phase of the vibration is irrelevant, what is significant is the pattern of nodes and anti-nodes. Since it is the nodes of the vibration which represent perceived edges or grouping percepts in the model, a more convenient form to express these waveforms mathematically is as nodal functions Nq which are given by
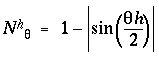
|
(EQ 6) |
as shown in figure 12 C. In other words these functions are computed by subtracting the wave forms in figure 12 B from unity, because this encodes the features, i.e. the edges, as positive values rather than as the absence of positive values.The positive peaks in these waveforms now represent the patterns of perceived edges or grouping percepts as shown in figure 12 A. An offset value c was added to these nodal functions in order to shift them half way into the negative region as shown in the plot, with the offset value chosen so as to make the nodal functions sum to zero, i.e to produce equal areas under positive and negative regions of the curve. This was done so that when used as convolution filters they do not impose a bias on the output. The normalized nodal functions are given by
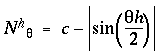
|
(EQ 7) |
with c = 1.63662. Figure 12 D plots these nodal waveforms on a circular plot, whose outer ring represents the value +1, the inner ring represents the value -1, and the middle ring represents the value zero.
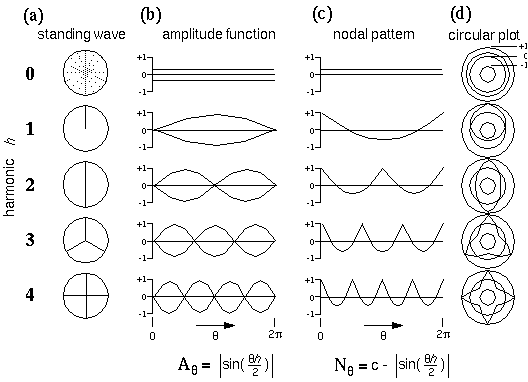
Directional Harmonic representation. (a) Various patterns of nodes on a circular plate corresponding to the different harmonics of directional periodicity of the plate. The black lines represent the nodes, or stationary points of the standing wave, which in turn correspond to various configurations of edges that meet at the center, to define a sequence of vertex types. (b) The amplitude function, or variation of the amplitude of vibration as a function of angle around the circular plate. (c) The nodal pattern, or ones- complement of the amplitude function, to produce positive peaks in place of the nodes seen in the amplitude function. (d) A circular plot of the nodal pattern, where the inner circle represents the value -1, the outer circle represents +1, and the middle circle represents zero.
The circular harmonic response Rhq to the input signal at each dot location is then computed by a circular convolution of the circular input signal Iq with each of these circular harmonic nodal filters Nhq in turn, for each harmonic h = 1 to 4, as given by
|
(EQ 8) |
where (q + r) is computed modulo 2p to wrap around the full circle. This produces a set of harmonic responses Rhq to the input, one for each harmonic h, each response being a circular function through q = 0 to 2p, which represents the response to the input for that particular harmonic. As is the case with any convolution, the magnitude of each directional harmonic response is a function of the similarity, or degree of match between the functional form of that particular harmonic and the pattern of the input. For example an input function I with a single peak extending in one direction will produce a strong response R1 to the first harmonic filter N1, and the peak of that response function will be aligned with the peak in the input, while an input function with two peaks separated by 180 degrees will produce a strong response R2 to the second harmonic filter N2, etc. The four harmonic responses interact with each other by constructive and destructive interference as calculated by summation, producing a total harmonic response Rq across all four harmonics which is computed as
|
(EQ 9) |
for h = 1 to 4. In other words, wherever positive peaks from different harmonics coincide, they summate by constructive interference to produce a larger positive peak, whereas positive and negative peaks from different harmonic responses cancel each other by destructive interference to produce the total or resultant harmonic response. It is this total response to all harmonics of directional periodicity which corresponds to the predicted perceptual grouping at each dot location in response to the presence of adjacent dots.
I will now present computer simulations of very simple dot stimuli composed of only two or three dots, to demonstrate how the harmonic response is calculated for these simple cases, before proceeding to more interesting cases involving more complex patterns of stimulus dots. Figure 13 demonstrates the computation of the circular harmonic response at a central dot location in response to a single neighboring dot in the 12 o'clock direction, as shown in figure 13 A. The input signal Iq due to that dot exhibits a single peak in the 12 o'clock direction, as shown in figure 13 B. Each of the filters Nhq of figure 12 D is convolved with the input signal Iq to produce the set of responses Rhq shown in figure 13 C as defined in equation 8. The first harmonic R1q (solid line plot) produces a positive response in the 12 o'clock direction, with a sharp positive peak at 0 degrees, and a broad negative trough through 180 degrees. The second harmonic R2q (dashed line plot) produces a double peaked response, with sharp positive peaks at 0 and 180 degrees, and broad negative troughs through 90 and 270 degrees. The third harmonic R3q (dash-dot line plot) produces a three-peaked response, with positive peaks at 0, 120, and 240 degrees, and negative troughs in between, and the forth harmonic R4q (dotted line plot) produces four positive peaks at 0, 90, 180, and 270 degrees, with negative troughs at the diagonals. The harmonic response to this single peaked input signal is similar to the impulse response, or point-spread function of the system, which is why the response of each harmonic to this particular input is virtually identical to the shape of the waveform of the harmonic itself. The total harmonic response to this input Rq is then calculated by summing all of the four harmonic responses at every direction as defined in equation 9, which results in the combined harmonic response shown in figure 13 D. The positive portion of this response (shaded) points upwards in the direction of the input dot, and this response in turn represents a grouping percept extending upward from the lower dot towards the upper dot. By symmetry, the harmonic response at the upper dot (not plotted) would be identical except rotated by 180 degrees, i.e. with a grouping percept extending downward towards the first dot. If the calculation were extended to include higher harmonics, the irregular response profile of figure 13 D would become progressively smoother in the negative portion and sharper in the positive peak, eventually matching the shape of the input function itself. In other words the irregular pattern of peaks in the negative range in figure 13 D reflect the quantization due to the fact that only the lowest four harmonics were computed in the simulation.
Harmonic response to a single vertically adjacent dot (a) is computed by a circular convolution of the circular input signal (b) with a set of circular nodal functions. This produces a set of circular harmonic response functions (c). The final perceptual grouping is computed as a sum of these response functions, as shown in (d), where the positive portion (shaded) represents the actual grouping percept.
Figure 14 introduces a spatial plotting convention to give a more intuitive depiction of the perceptual grouping predicted by the model, with input and harmonic response functions displayed for every dot in the stimulus rather than only for one central dot. Figure 14 A shows two vertically adjacent dots, as before. Figure 14 B shows the input signal at each dot, plotted as before, but this time overlaid on the spatial plot of that same input signal. In the spatial plot, the magnitude of the circular input signal at each dot is depicted as a grey shading extending radially outward from the dot, the darkness of the gray shading representing the magnitude of the input signal in each direction. The shading fades with distance from the dot by the same Gaussian function as that used in computing the input signal for that dot. For example the lower dot in figure 14 B has a strong peak in its input function at the 12 o'clock direction, and this is depicted in the spatial shading convention as a region of dark shading projecting from the dot in the 12 o'clock direction, and fading with distance from the dot. The upper dot exhibits a similar input signal projecting downwards in the 6 o'clock direction. Figure 14 D through F plot the same data as in figure 14 A through C, except this time showing only the spatial shaded plot without the circular plot overlay. The gray shading in the input plot of figure 14 B and E suggest the pattern of perceptual grouping which would be predicted by a grouping-by-proximity model, in which the strength of grouping between any pair of dots is a simple Gaussian function of the distance between them. Figure 14 C and F show the harmonic response function computed for each dot as above, and displayed with the spatial shading convention. Since it is only the positive values of the harmonic response function which correspond to predicted perceptual grouping, only positive values are plotted in the spatial plot. It is in this plot that the subtle and interesting predictions of the Directional Harmonic model manifest themselves, although in this simple case there is no significant difference between the prediction of the harmonic resonance model and a simple grouping by proximity model.
A spatial plotting convention to give a more intuitive depiction of the depicted perceptual grouping, showing the harmonic responses for all dots in the stimulus simultaneously. (a) A pattern of two adjacent dots. (b) The input signal at each dot location due to the presence of the other dot, produces a peak in the input plot in the direction of the other dot, and that peak is displayed both as a circular plot, and as a gray radial shading. (c) The harmonic response plotted for each dot in the stimulus, again plotted both as a circular plot, and as a gray shading in the direction of the positive peaks of the plots. In this simple case the harmonic response is very similar to the input signal. (d, e, and f) The same as plots (a, b, and c) except this time showing only the gray shading, without the circular plot overlay. The harmonic response shown in (f) represents the predicted grouping percept for this configuration of dots, in this case predicting a first harmonic, or "end stop" feature grouping at each dot location.
Figure 15 depicts a slightly more complex stimulus, with three dots in a vertical line. Figure 15 A depicts the stimulus dot pattern relative to the central dot (circled), and figure 15 B depicts the input response at the central dot. Figure 15 C depicts the response of the first four harmonics of directional periodicity to this input pattern. In this case the response is dominated by the second harmonic, with positive peaks in the 6 and 12 o'clock directions. There is a weaker response of the fourth harmonic, with positive peaks at 6 and 12 o'clock, but the absence of dots in the 3 and 9 o'clock directions keeps this response weaker than the second harmonic response. The third harmonic produces only a very weak response, because its positive and negative peaks are separated by 180 degrees, so when the positive lobe of the filter is aligned with one input peak, the negative lobe is aligned with the other input peak. The same is true also for the first harmonic, which also produces a very weak response. Figure 15 D depicts the total harmonic response, which produces positive peaks in the 6 and 12 o'clock directions due to both the second and fourth harmonics, and small peaks in the 3 and 9 o'clock directions due to the fourth harmonic, but since these peaks are opposed by negative peaks in the second harmonic, the total harmonic response remains negative in those directions. The grouping percept predicted by the directional harmonic model in response to this stimulus therefore is a second harmonic or collinear grouping, with grouping lines projecting upward and downward toward the adjacent dots. Figure 15 E, F, and G depict the spatial plot for this same stimulus. Note that the harmonic responses at the upper and lower dots are dominated by the first harmonic, i.e. with an illusory grouping line projecting downward and upward respectively toward the central dot, similar to the grouping seen in figure 14. Again, in this simple case the prediction of the directional harmonic model is not very different from the input signal itself, which is the kind of grouping which would be predicted by a simple grouping-by- proximity model.
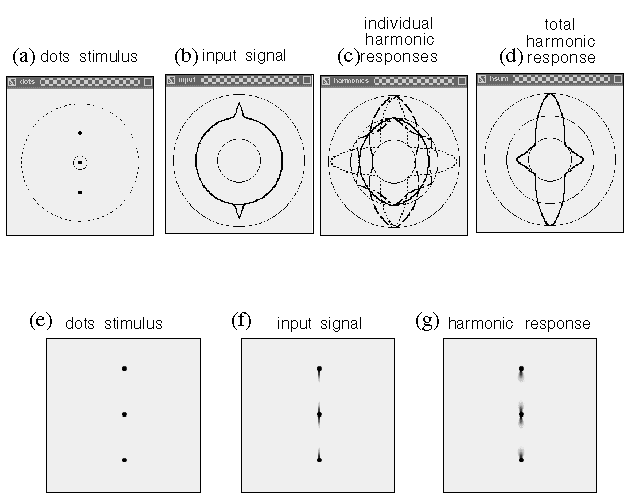
(a through d) Computer simulation of the harmonic response of a dot flanked by two neighboring dots in a straight line. (a) the pattern of dots in the stimulus. (b) The input response at the central dot, showing peaks at 6 and 12 o'clock. (c) The individual harmonic responses to this input at the central dot location, showing a strong second harmonic response, and a weaker fourth harmonic response, and still weaker first and third harmonic responses. (d) The total harmonic response for this stimulus at the central dot location, showing positive peaks at 6 and 12 o'clock, dominated by the second harmonic or collinear grouping percept at the central dot. (e through g) A computer simulation of the grouping between three dots in a vertical column, showing (e) the input dot stimulus, (f) the input function and (g) the total harmonic response at each dot location using the spatial plotting convention. This simulation therefore predicts a collinear grouping through the middle of this column of dots, with end-stop groupings at the top and bottom dots.
Figure 16 shows the computer simulations for all of the dot grouping patterns of figure 4. The three columns in figure 16 represent the dot pattern used in the simulation, the input signal computed for each dot, and the directional harmonic response due to that input signal computed at every dot location. Figure 16 A shows the grouping between pairs of dots, which produces primarily a first harmonic response, as seen in figure 4 A. Figure 16 B shows the collinear grouping along vertical lines of dots, as seen in figure 4 B. This grouping is due to a second harmonic response at each dot location, although a lateral or fourth harmonic response is also in evidence. The terminal dots at the top and bottom of each column of dots exhibits a first harmonic response. Figure 16 C simulates the hexagonal grouping percept observed in figure 4 C, due to a third harmonic response at each dot location. It is in this more complex stimulus that the directional harmonic model demonstrates its predictive power. Prominently absent from the harmonic response are the vertical, horizontal, and diagonal grouping percepts that are in evidence in the input response at each dot location. Figure 16 D shows the four-way or orthogonal grouping percept corresponding to figure 4 D, due to a fourth harmonic response at each dot location. Again, prominently absent from the harmonic response is the diagonal grouping which is in evidence in the input signal for this stimulus.
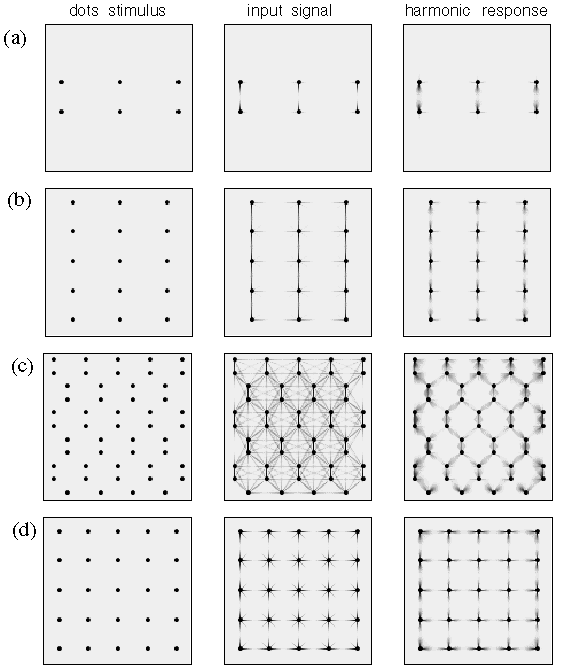
Computer simulations of the four dot grouping phenomena shown in figure 4, showing for each dot pattern the stimulus configuration, the input signal at each dot location, and the harmonic response at each dot location using the spatial plotting convention. (a) The pairs of dots form end-stop grouping percepts to the adjacent dot. (b) The columns of dots promote a vertical collinear grouping along the columns. (c) The hexagonal dot grouping dominated by a third harmonic response at each dot location. (d) A grid-like percept due to dominance of the fourth harmonic grouping.
When a vertical column dot stimulus like that in figure 4 B is varied parametrically by shifting alternate rows of dots to the right, the perceptual experience due to that grid of dots exhibits characteristic transitions, sometimes abrupt, between different perceptual grouping patterns. Figure 17 shows these transitions as a spatial rather than a temporal sequence. The alternate rows of dots in figure 17 have been shifted by a shift value of zero on the left side of the figure (i.e. no shift at all) to a value of 0.5 on the right side of the figure, expressed in units of the horizontal dot spacing, i.e. a shift of 0.5 means that the alternate rows of dots have been shifted half way to the next adjacent column. The resulting perceptual experience can be categorized as a vertical column or linear grouping percept, as seen in figure 17 A, where the shift value is very small. This then gives way to a zig-zag grouping as seen in figure 17 B, in which each column is perceived to be composed of a series of sharp angles. As the shift value is further increased the percept becomes somewhat ambiguous, before finally settling into a more stable diagonal grouping, or cross-hatch pattern, as seen in figure 17 C. Figure 18 shows computer simulations of these various grouping patterns. The abrupt transitions between distinct grouping percepts seen in this figure reveal the influence of the directional harmonic resonance, because these transitions appear only in the harmonic response image, whereas the input signal exhibits only a gradual or continuous transition between these arrangements of the stimulus. The abruptness of these perceptual transitions therefore mark a significant difference between the predictions of the Directional Harmonic model and a simple grouping-by-proximity model.
rectangular dot grid pattern in which alternate rows are shifted to the right, where the amount of shift varies continuously from the left to the right side of the figure. Perceptually, this shifting segments the percept into three distinct regions, that exhibit a (a) vertical linear, (b) zig-zag, and (c) cross-hatch grouping percept as a function of shift.
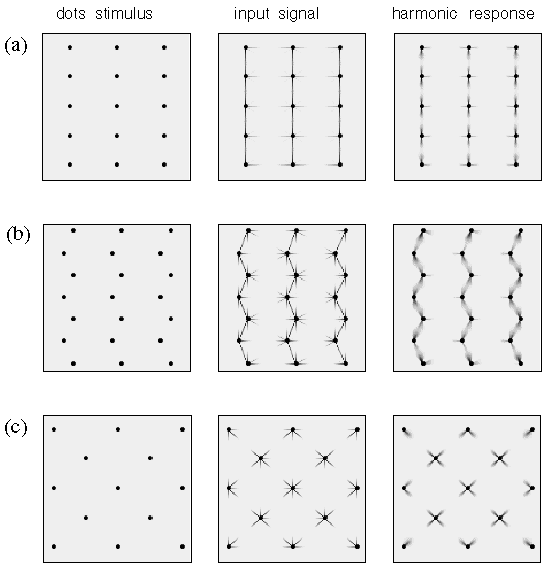
Computer simulation of the three perceptual groupings observed in figure 19. (a) Collinear grouping of columns, dominated by the second harmonic grouping. (b) Wavy line grouping where each dot marks the center of a two-armed vertex. (c) Cross-hatch grouping in which every dot marks the center of a diagonal fourth harmonic or "X" grouping percept.
The different grouping patterns seen in figure 17 can be explained by the directional harmonic model as the successive dominance of different harmonics of the grouping mechanism at different shift values. Figure 19 shows a computer simulation of the directional harmonics at a central dot location between two adjacent dots, as the flanking dots are progressively deflected from a collinear configuration. In figure 19 A the flanking dots are deflected 15 degrees downwards from the horizontal, i.e. the three dots form an internal angle of 150 degrees. At this small angle of deflection the harmonic response is still dominated by the second harmonic, i.e. the dots are perceived to be in a collinear alignment. In figure 19 B the deflection has been increased to 30 degrees, so the internal angle between the dots is now 120 degrees. In this configuration the response is dominated by the third harmonic, i.e. the dots are perceived to form an obtuse angle. The third harmonic response has a third branch, besides the two aligned with the flanking dots, which suggests a tendency for a perceptual grouping line to emerge in that direction. However this tendency is balanced by the first harmonic, which exhibits a positive peak downwards, and a negative trough upwards in figure 19 B, as well as by a negative trough in the fourth harmonic, which is why the combined harmonic response shows no positive peak in the 12 o'clock direction. Figure 19 C shows the angle of deflection now increased to 45 degrees, so that the dots now define a right angled corner. This in turn promotes the fourth harmonic as the dominant response of the system. The fourth harmonic response exhibits two additional peaks besides the two aligned with the neighboring dots, which are almost positive in the combined harmonic response shown in figure 19 C. The presence of adjacent dots in exactly those directions in figure 18 C is enough to boost those peaks to positive values, resulting in a fourth harmonic or four-way grouping percept at each dot.
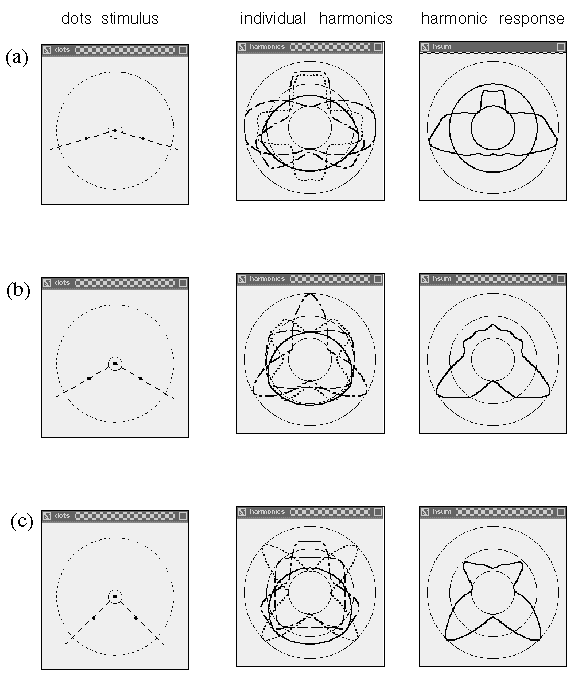
Simulation of kinking of a perceived line of dots with increased curvature, as seen in figure 2 c and d. (a) Three dots in a line with a slight downward deflection (dashed lines) promotes a predominantly second harmonic or collinear groupin gpercept. (b) three dots with a greater deflection produce harmonic responses in which the third harmonic response dominates. (c) When the angle between the dots approaches 90 degrees, the fourth harmonic dominates, with a tendency to form illusory grouping lines in all four directions of the fourth harmonic vertex.
The competition between different harmonics in response to various dot configurations also offers an explanation for the abrupt kinking of a line or circle of dots, as seen in figure 3 B and C, which is observed to occur just as the angle between three adjacent dots approaches 120 degrees, the angle which favors the third harmonic response. Again these quantized, or abrupt perceptual transitions in response to a continuous parametric variation of the stimulus are due to the loss of the higher harmonics due to impedance, which in turn results in the perceptual characterization of these stimuli in terms of various combinations of the lower order terms, which serve as a basis set of geometrical primitives for encoding the perceived forms.
rectangular dot grid in which alternate pairs of rows are shifted horizontally to produce (a) linear, (b) wavy line, and (c) hexagonal grouping percepts.
Figure 20 demonstrates a different parametric variation of a dot grid pattern, this time obtained by shifting alternate pairs of rows by a variable amount. This leads to distinct perceptual grouping patterns which can be categorized as linear, wavy, and hexagonal grouping percepts with progressively increasing shift value. Figure 21 shows how these patterns too can be explained by the directional harmonic model. The wavy pattern gives way to the hexagonal pattern at the point where the third leg of the third harmonic grouping percept at each apex (see in figure 21 B) comes into alignment with those on the adjacent column of dots, forming a bridge that spans the gap between the columns, resulting in the hexagonal grouping percept of figure 21 C.
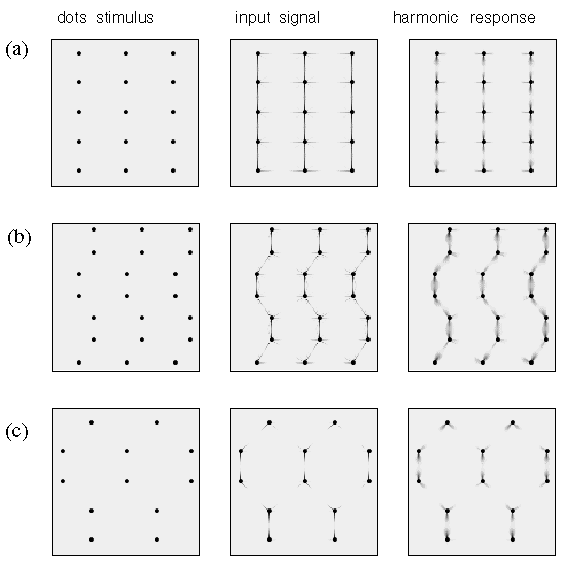
Computer simulation of (a) the collinear grouping, (b) the wavy line percept, and (c ) the hexagonal grouping percept seen in figure 22.
In the dot grouping simulations presented above, the input to the system at each dot location was assumed to energize the directional harmonic resonance at that location with equal energy at all orientations. The final pattern of resonance therefore results exclusively from the configuration of neighboring dots, as communicated through the angular and radial Gaussian input functions. A line segment stimulus on the other hand provides an oriented input signal along the line segment, corresponding to a second harmonic or collinear grouping at every point along that line. This raw input is expected to overwhelm the resonance at every point along that line, resulting in a strong second harmonic response along the stimulus lines, corresponding to a collinear "grouping" percept, or the veridical percept of the stimulus line as a line of the appropriate orientation. The interesting grouping effects observed in the line segment stimuli are observed at the line endings, where each line ending behaves somewhat like a dot stimulus, except with an oriented bias, or strong oriented input in the direction of the line segment. The line pattern grouping simulations of the directional harmonic model are therefore performed similar to the dot pattern groupings, in that the harmonic resonance is computed only at the points where the line segments terminate, i.e. at the line endings, as shown in figure 22 A. The resonance at the line ending is therefore biased by a fixed oriented input signal from the line of which it is the terminus. For example the point at the top end of a vertical line segment is assumed to have a permanent input signal from the 6 o'clock direction, in addition to any other influences from adjacent line endings, whereas the bottom end of a vertical line segment has a permanent input from the 12 o'clock direction, as shown in figure 22 A. The model can also be used to simulate vertices, as shown in figure 22 B, in which case the input signal at the vertex is assumed to have permanent inputs from the directions of the component line segments of that vertex, as shown in figure 22 B. With this simple addition, the directional harmonic model now also accounts for the perceptual line segment grouping phenomena shown in figure 5.
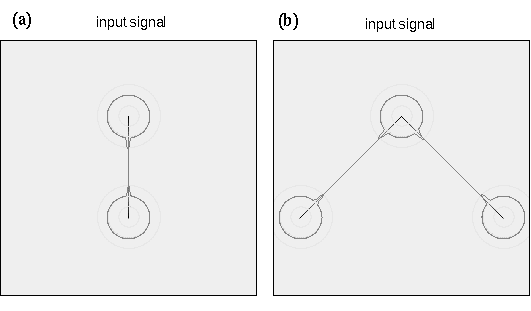
(a) The directional harmonic simulations of line segment stimuli are performed similar to those of the dot patterns, with the harmonic response being calculated only at the location of the line endings. The input signal at each line ending is presumed to have a permanent input signal from the direction of the line of which that point is the terminus. For example the top end of a vertical line segment is presumed to have a permanent input signal from the six o'clock direction, while the bottom end would have a permanent input signal from the 12 o'clock direction as shown here. (b) In the case of multiple line segments, the harmonics are computed at each vertex, where a permanent input signal is presumed in the direction of each of the component line segments as shown here.
Figure 23 A through C shows the directional harmonic simulation for collinear, orthogonal, and diagonal grouping respectively of the line segment stimuli, as observed perceptually in figure 5 A through C. The collinear grouping percept shown in figure 5 A is explained by a second harmonic response at each line ending, as shown in figure 23 A. The significant difference between the resonance response and the input signal (equivalent to the prediction of a grouping-by-proximity model) is not so much the predominantly vertical grouping, which is observed in both responses, but in the suppression of the alternative horizontal and diagonal groupings observed in the input signal. The orthogonal grouping percept of figure 5 B is explained by a fourth harmonic grouping at each line ending in figure 23 B, with attenuated grouping percepts in the collinear and diagonal directions, whereas the diagonal grouping percept of figure 5 C is explained by a third harmonic or "Y"-vertex response at each line ending, as seen in figure 23 C, with a suppression of the horizontal, and extraneous diagonal groupings observed in the input signal for that stimulus.
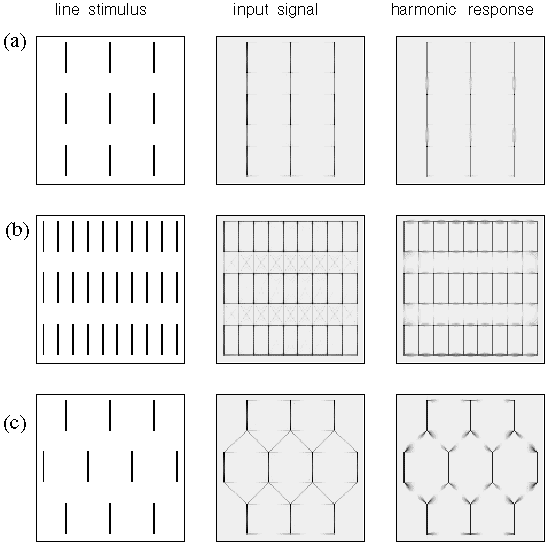
Computer simulations of perceptual grouping between line segment stimuli, showing (a) collinear grouping, (b) orthogonal grouping, and (c) diagonal grouping percepts at each line ending.
The most appealing aspect of the Directional Harmonic Theory is not so much in the details of any one of its subtle and tenuous predictions of perceptual grouping, but in the great diversity of different perceptual grouping phenomena which are all consistent with those predictions. And those phenomena cover a repertoire of collinear, orthogonal, and a variety of illusory vertex types, together with the cooperative and / or competitive interactions between those various grouping tendencies. The orthogonal grouping percept in figure 23 B offers an explanation for the amodal component of the Ehrenstein illusion, shown in figure 24 A. The same model also replicates the amodal grouping observed in the shifted line grid stimulus of figure 2 C, as shown in figure 24 B. The model also replicates a diagonal grouping percept in the zig-zag line grid stimulus as shown in figure 24 C, and it also accounts for an orthogonal grouping between parallel lines which are slanted relative to the grouping percept, as shown in figure 24 D. Again, the simple grouping-by- proximity model also predicts the principal groupings here, but the subtle refinement of those predictions in the Directional Harmonic simulation is seen in the suppression of the alternative grouping percepts seen in the input signal. For example the input signal for the Ehrenstein figure includes grouping lines between non- adjacent line endings, which are suppressed in the harmonic response image; the input signal for the zig-zag line grid stimulus exhibits faint vertical grouping percepts which are suppressed in the harmonic response; and the input signal for the slanted line grid stimulus exhibits collinear and diagonal groupings which are suppressed in the harmonic response. More generally, given the operational principle of the Directional Harmonic model, all of these groupings can be seen as evidence for the tendency of the visual system to enhance or amplify the directional periodicity of visual elements in the stimulus. The most general prediction of the Directional Harmonic model therefore is that arrays of dots or line segment stimuli will promote the most salient grouping percept when they are arranged so as to maximize one or another harmonic of directional periodicity.
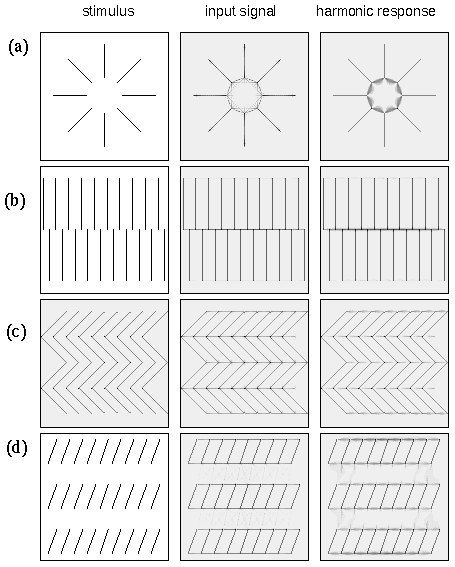
Computer simulations of (a) the Ehrenstein figure, (b) the shifted line grid stimulus, (c) a zig-zag line grid stimulus, and (d) an orthogonal grouping between slanted line segments. Although the input signal images which represent the prediction of a simple grouping-by-proximity model also replicate the major features of these illusions, the refinement offered by the harmonic response is seen in the suppression of alternative weaker grouping percepts.
The Directional Harmonic model also replicates the perceptual phenomenon shown in figure 3 B, where the percept of a circle of dots changes to a polygon of dots as the number of dots is reduced. According to the Directional Harmonic model, the critical factor here is not so much the size of the circle, but the angular deviation of the line through the dots. (The size of the circle is varied to keep the dot spacing constant.) The explanation for this effect can be seen in figure 19, as the successive dominance of different harmonics of directional periodicity as the angle of the vertex is progressively bent from a collinear 180 degrees in figure 19 A, to a right angled vertex in figure 19 C. Perceptually, the interpretation of the configuration of dots as a second harmonic collinear grouping in figure 19 A is accompanied by additional energy consistent with that harmonic, seen in the harmonic response image in figure 19 A as extra energy towards the three- and nine o'clock directions, completing the perceptual grouping as being more collinear than the actual configuration of dots. The opposite effect is seen in the third harmonic grouping shown in figure 19 B, where extra energy is seen in the harmonic response plot in the four- and eight o'clock directions, due to the combined influence of the third and fourth harmonics. In other words as the line of dots is deflected progressively from a horizontal alignment, the perceptual interpretation of that line of dots first lags behind, as if attempting to remain collinear, and then abruptly kinks to an angle which now inclines towards a sharper vertex, like the kinking of a drinking straw that is bent beyond its elastic limit. This very subtle perceptual effect, visible in figure 19, is barely discernible in the computer simulations of figure 25. But this same discontinuity, or abrupt transition in the perception of curvature has also been detected psychophysically as a tendency to underestimate curvature for small curvature values, and to overestimate curvature for larger curvature values (Wilson & Richards 1989), and the transition between these two modes of curve detection occurs at about the same point as predicted by the Directional Harmonic model, i.e. where the second harmonic gives way to a third harmonic grouping.
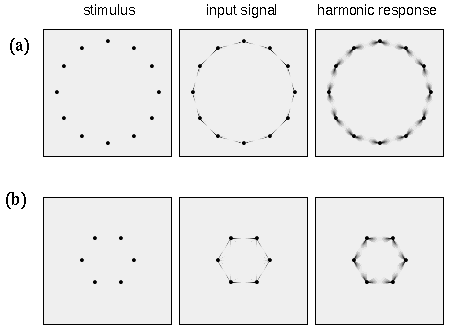
(a) Directional Harmonic simulations of a circle of dots, which gives way to a percept of (b) a polygon of dots, when the number of dots in the circle is small enough.
Ever since Santiago Ramon y Cajal discovered the cellular basis of the nervous system, the idea of the nervous system as an assembly of quasi-independent processors, sometimes called the Neuron Doctrine (Barlow 1972, 1995), has become firmly established as the dominant paradigm of neurocomputation. Many different arrangements of these simple integrate-and-threshold elements have been tried in computer simulations in an attempt to coax some kind of interesting or suggestive behavior from them as an explanation for perceptual processing. But certain aspects of perceptual function have remained so elusive as to cast doubt on the entire enterprise. Particularly problematic have been the enigmatic properties of perception identified by Gestalt theory. The principle of invariance is ubiquitous in many aspects of perception, including invariance in the recognition of simple shapes to rotation, translation, and scale. And yet this kind of invariance is very difficult to achieve in conventional neural network models, for it leads to a combinatorial explosion in the required number of receptive fields. The principle of emergence, identified by Gestalt theory, is also problematic for neural network models, because it suggests a relaxation to equilibrium of a massively parallel dynamic system through many iterations, a concept which is difficult for the Neuron Doctrine given the time delays inherent in the chemical synapse. There is also a dimensional mismatch between the continuous field-like nature of perceptual experience identified by Gestalt theory, and the constellation of discrete activations of individual neurons in the Neuron Doctrine (Lehar 2002). I propose therefore to go all the way back to the debate between Golgi and Cajal, and to reconsider the question of whether the essential principles of neurocomputation are best described as an atomistic system of simple quasi-independent local processors as suggested by neural network theory, or as a holistic continuous field- like principle as suggested by Gestalt theory. I don't propose to question the neurophysiological and histological evidence for the cellular basis of the nervous system, or for the properties of the chemical synapse. However I do contest the significance of that evidence for the essential principles of neurocomputation.
In fact the problems with the Neuron Doctrine date as far back as the development of the first brain recording technique, the electroencephalogram (EEG). From the outset the EEG detected a global oscillation across the whole brain, and that global synchrony was found to correlate with particular functional states. However the significance of this global resonance remains to this day as mysterious as it was when it was first discovered. Now with the introduction of multiple-unit recordings, this global resonance is even beginning to manifest itself in electrophysiological data. Although it is not much discussed in the contemporary literature, this kind of global resonance is problematic for the Neuron Doctrine. For the phasic spiking of a neuron is unlikely to survive across the chemical synapse, due to the multiple parallel paths in each axonal and dendritic arborization, each with variable path lengths and dendritic diameters which would introduce random time delays across all those parallel paths, not to mention the temporal averaging of the signal in each of the 10,000 or so parallel chemical synapses that connect a typical pair of neurons. After the third or fourth such transmission along a line of cells, the phasic pulses of the neural signal would surely diffuse into a featureless blur, which would preclude the kind of global synchrony observed in the EEG signal across the cortex as a whole.
Another Achilles heel in the Neuron Doctrine that receives little mention today, is the fact that the cell membrane, although capable of insulating electrical charge inside the cell, does not insulate alternating currents. For like the insulating dielectric in a capacitor, the cell wall transmits alternating current signals perfectly well, and blocks only direct current. That is why single-cell electrode recording can be performed extra-cellularly, just as well as intra-cellularly. This in turn suggests that the alternating current spiking signal of the neuron is likely to propagate directly from cell to cell across the extracellular matrix, unhindered by the insulation of the cell membrane. Pribram (1971) proposes that the overt spiking of the neuron is not the causal origin, but merely a secondary manifestation or response of the cell to a graded potential oscillation that pervades the body of neural tissue, because that oscillation has been observed to continue even after the spiking cell falls below threshold and ceases to fire. Like whitecaps on ocean waves, the spiking neuron merely reveals the presence of a more subtle underlying resonance that pervades the bulk neural tissue. The reason that this graded potential oscillation has received so little attention in electrophysiological circles has been for lack of a theoretical framework to give meaning to those resonances, or to explain how harmonic resonance can perform a computational function in the brain.
I propose that the global synchrony observed in the EEG recordings, and now in the synchronous activity of cortical neurons, is exactly what it appears to be, i.e. it is a manifestation of a global harmonic resonance that pervades the entire cortex, and that this resonance subserves a computational function which is central to the principle of operation of the brain (Lehar 1994a, 1994b, 1999, 2002). The purpose of this resonance is to set up a pattern of standing waves, and these standing waves serve a function which is normally ascribed to spatial receptive fields in neural network models, i.e. as a mechanism for encoding spatial patterns in the brain both for recognition and for perceptual completion.
The computational function performed by these standing waves is highlighted in the Directional Harmonic model by comparison with the functionally equivalent neural network models that it replaces. The second harmonic standing wave of directional periodicity mirrors the functionality of a collinear completion model as proposed by Grossberg & Mingolla (1985, 1987), Walters (1987), and Zucker et al. (1989), except that functionality no longer requires separate spatial receptive fields replicated at every location and every orientation across the visual field, but rather, the second harmonic resonance emerges spontaneously at the location and orientation determined by the stimulus. Furthermore, this same dynamic resonance also performs perceptual completion through a range of different vertex types corresponding to the various harmonics of directional periodicity, such as "Y" and "+" or "X" vertices, with no additional hardware required. But even that does not exhaust the computational repertoire of the Directional Harmonic model, for as in a Fourier representation, these harmonics are also used in combination to produce compound standing wave patterns corresponding to "L" and "T" and "V" vertices. This is functionally equivalent to a neural network model capable of merging different receptive field profiles into new compound receptive fields on the fly, and using those compound fields to perform completion of spatial patterns.
Finally, there is one further aspect of a harmonic resonance theory that deserves mention, and that is its relation to emergence and reification in Gestalt illusions. The neural network models of Grossberg & Mingolla (1985, 1987), and Zucker et al. (1989) incorporate an explicit top-down feedback from what I have called the "feedback layer" back down to the layer of local oriented edge detectors, so that the higher level groupings computed in the feedback layer are expressed back at the oriented edge layer as explicit edge percepts. This is done in order to account for the perceptual experience of a sharp high resolution contour in figures like the camo and the Kanizsa triangles, at a location where there is no edge present in the stimulus. Although this issue was not addressed explicitly in the Directional Harmonic model, it is in the very nature of harmonic resonances in adjacent sub-systems to tend to couple with each other by mutual reciprocal feedback to produce a single combined resonance. A resonance model therefore does not have to add top-down feedback of this sort as an explicit mechanism of the model, because it is already a natural property of the resonance itself. (Lehar 1999) In fact this natural tendency of individual local resonances to couple into a single global resonance is, I propose, the central operational principle behind the holistic global nature of Gestalt phenomena. In other words harmonic resonance offers a computational principle that exhibits the holistic global aspects of perception identified by Gestalt theory, not as specialized mechanisms or architectures contrived to achieve those properties, but as natural properties of the resonance itself. The principal value of the Directional Harmonic Theory therefore is not so much as evidence for some kind of resonance in the brain, for that evidence already exists from a wide variety of diverse sources. But rather the Directional Harmonic Theory offers a specific and detailed model of exactly how standing waves might perform a computational function in perception normally ascribed to spatial receptive fields, and demonstrates how that function circumvents some fundamental limitations inherent in the template-like concept of the neural receptive field, by an emergent holistic process consistent with Gestalt theory.
Banton Tom, & Levi Dennis (1992) The Perceived Strength of Illusory Contours. Perception & Psychophysics, 52, 676-684.
Barlow H. B. (1972) Single Neurons and Sensation: A neuron doctrine for perceptual psychology. Perception. Perception 1, 371-394.
Barlow H. B. (1995) The Neuron Doctrine in Perception. In M. Gazzaniga (Ed.), The Cognitive Neurosciences. Cambridge: MIT Press.
Biederman I. (1987) "Recognition-by-Components: A Theory of Human Image Understanding". Psychological Review 94 115-147
Bremer F. (1953) "Some Problems in Neurophysiology". London: Athlone Press.
Chladni, E. E. F. (1787) "Entdeckungen Über die Theorie des Klanges". Leipzig: Breitkopf und Härtel.
Dennett D. 1991 "Consciousness Explained". Boston, Little Brown & Co.
Dennett D. 1992 "`Filling In' Versus Finding Out: a ubiquitous confusion in cognitive science". In "Cognition: Conceptual and Methodological Issues, Eds. H. L. Pick, Jr., P. van den Broek, & D. C. Knill. Washington DC.: American Psychological Association.
Eckhorn R., Bauer R., Jordan W., Brosch M., Kruse W., Munk M., Reitboeck J. (1988) "Coherent Oscillations: A Mechanism of Feature Linking in the Visual Cortex?" Biol. Cybern. 60 121-130.
Gerard, R. W. & Libet B. (1940) "The Control of Normal and `Convulsive' Brain Potentials". Amer. J. Psychiat., 96, 1125-1153.
Grossberg, Stephen, & Mingolla, Ennio (1985). Neural Dynamics of Form Perception: Boundary Completion, Illusory Figures, and Neon Color Spreading. Psychological Review, 92, 173-211.
Grossberg, Stephen, & Mingolla, Ennio (1987). Neural Dynamics of Surface Perception: Boundary Webs, Illuminants, and Shape-from-Shading.. Computer Vision, Graphics and Image Processing, 37, 116-165.
Grossberg, Stephen, & Todorovic, Dejan (1988). Neural Dynamics of 1-D and 2-D Brightness Perception: A Unified Model of Classical and Recent Phenomena. Perception and Psychophysics, 43, 241-277.
Hashemiyoon R. & Chapin J. (1993) "Retinally derived fast oscillations coding for global stimulus properties synchronise multiple visual system structures". Soc. Neurosci. Abstr. 19 528.
Kanizsa, Gaetano (1987). Quasi-Perceptual Margins in Homogeneously Stimulated Fields.. In The Perception of Illusory Contours, Petry S. & Meyer, G. E. (eds) Springer Verlag, New York, 40-49.
Kellman P., J. & Shipley T. F. (1991) A Theory of Visual Interpolation in Object Perception. Cognitive Psychology, 23, 141-221.
Koffka K, (1935) "Principles of Gestalt Psychology" New York, Harcourt Brace & Co.
Lehar S. (1994a) "Directed Diffusion and Orientational Harmonics: Neural Network Models of Long-Range Boundary Completion through Short-Range Interactions". Ph.D. Thesis, Boston University. Available at http://cns-alumni.bu.edu/~slehar/webstuff/thesis/thesis.html
Lehar S. (1994b) "Harmonic Resonance in Visual Perception Suggests a Novel Form of Neural Communication. rejected Perception & Psychophysics 1995. Available at http://cns-alumni.bu.edu/~slehar/webstuff/pnp/pnp.html
Lehar S. (1999) "Harmonic Resonance Theory: an Alternative to the `Neuron Doctrine' Paradigm of Neurocom putation to Address Gestalt properties of perception." Rejected Psychological Review November 1999. Available at http://cns-alumni.bu.edu/~slehar/webstuff/hr1/hr1.html
Lehar S. (2002) "TheWorld In Your Head: A Gestalt view of the mechanism of conscious experience." Mahwah NJ: Erlbaum (in press). Information available at http://cns-alumni.bu.edu/~slehar/webstuff/book/WIYH.html
Marr D, 1982 "Vision". New York, W. H. Freeman.
Michotte A., Thinés G., & Crabbé G. (1964) "Les complements amodaux des structures perceptives". Studia Psychologica. Lovain: Publications Universitaires. In Michotte's Experimental Phenomenology of Perception, G. Thinés, A. Costall, & G. Butterworth (eds.) 1991, Lawrence Erlbaum, Hillsdale NJ.
Murthy V., & Fetz E. (1992) "Coherent 25- to 35-Hz oscillations in the sensorimotor cortex of awake behaving monkeys". Proc. Natl. Acad. Sci. USA 89, 5670-5674.
Nicolelis M., Baccala L., Lin R., & Chapin J. (1995) "Sensorimotor encoding by synchronous neural ensemble activity at multiple levels of the somatosensory system". Science 268, 1353-1358.
O'Regan K. J., 1992 "Solving the `Real' Mysteries of Visual Perception: The World as an Outside Memory" Canadian Journal of Psychology 46 461-488.
Pessoa L., Thompson E., & Noë A. (1998) Finding Out About Filling-In: A guide to perceptual completion for visual science and the philosophy of perception. Behavioral and Brain Sciences 21, 723-802.
Prigogine I. & Nicolis G. (1967) "On symmetry-breaking instabilities in dissipative systems". J. Chem. Phys. 46, 3542-3550/
Selfridge O. G. (1959) Pandemonium: A Paradigm for Learning. In D. V. Blake & A. M. Uttley (Eds.) Proceedings of the Symposium on Mechanization of Thought Processes. London: H. M. Stationary Office, 511-529.
Singer W. & Gray C. (1995) Visual Feature Integration and the Temporal Correlation Hypothesis. Annual Review of Neuroscience 18, 555-586.
Singer W. (1999) Neuyronal Synchrony: A versatile code for the definition of relations? Neuron 24: 49-65.
Sompolinsky H., Golomb D., & Kleinfeld D., (1990) "Global processing of visual stimuli in a neural network of coupled oscillators". Proc. Natl. Acad. Sci. USA 87, 7200-7204.
Turing A. M. (1952) "The chemical basis of morphogenesis". Philos. Trans. R. Soc. London. B 237, 37-72.
Waller M. D. (1961) "Chladni Figures, A Study in Symmetry". London, G. Bell & Sons.
Walters, D. K. W. (1987) Rho-space: A neural network for the detection and representation of oriented edges. Program of the Ninth Annual Conference of the Cognitive Science Society. Hillsdale, NJ. Erlbaum, 455-460.
Welsh B. J., Gomatam J., & Burgess A. E. (1983) "Three-Dimensional Chemical Waves in the Belousov-Zhabotinski Reaction". Nature 304, 611-614.
Wilson, Hugh R. & Richards, Whitman A. (1989) Mechanism of Contour Curvature Discrimination. J. Opt. Soc. Am. A/ 6, 1.
Winfree A. T. (1974) "Rotating Chemical Reactions". Scientific American 230 (6) 82-95.
Zucker, Steven W., Dobbins, Allan, & Iverson, Lee (1989). Two Stages Of Curve Detection Suggest Two Styles Of Visual Computation. neural computation, 1, 68-81