Plato's Cave: Diffusion in FCS Model
Diffusion in FCS Model
The diffusion operation of the FCS model is a unique computational
mechanism. Its operation can be explained qualitatively with a
mechanical analog of a system of pumps which pump "darkness signal"
and "brightness signal" into the areas corresponding to the dark and
bright regions in the spatial derivative image. These signals are free
to diffuse spatially except across edges in the BCS (boundary) image,
which act as semi-permiable barriers to the diffusion, resulting in
"pooling" of the perceptual signal. A decay term throughout acts as a
slow leak of brightness and darkness signal.
For example, for an image of a white square on a black background, the
DOC image exhibits a contrast-sensitive edge representation of that
square, with a bright inner outline, and a dark outer outline, with
zero response in the uniform regions both within and without the
square. In our diffusion analogy, the BCS boundaries are represented
by a semi-permeable square boundary, with "brightness fluid" being
pumped in along the inner perimeter, and "darkness fluid" pumped in
along the outer perimeter of the square. Since these two "perceptual
fluids" do not interact, they can be considered as separate systems,
as shown below.
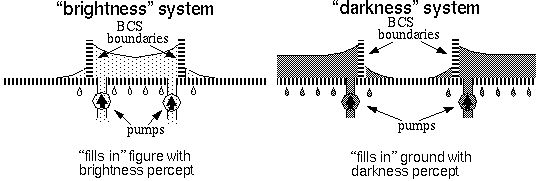
The brightness fluid will tend to "pool" or fill in the inner part of
the square, while the darkness fluid will fill in the outer part of
the square, filling in the entire background surface with darkness
percept. Some of the brightness and darkness fluids diffuse also
across the semi-permeable barrier, at a rate which is proportional to
the difference in fluid level across that barrier. The "floor" of our
mechanical analog is also made of semi-permeable stuff, so that a
steady stream of both brightness and darkness will leak out slowly
from below, at a rate that is proportional to the depth of the fluid.
This leakage represents the "decay term" in the differential equation,
which serves to reduce the percept to zero in the absence of
stimulation.
The system will reach a dynamic equilibrium therefore when the rate at
which fluid is leaking out through the boundaries and the floor, is
exactly balanced by the rate at which it is being pumped in along the
edges of the figure. The final state of this system therefore
represents a dynamic equilibrium with fluid flowing in and out at a
constant rate, and the final brightness percept is calculated for each
point in the image by the depth of "brightness fluid" minus the depth
of "darkness fluid" at that point.
Return to argument
Return to Steve Lehar

