Plato's Cave: The Feature Contour System
The Feature Contour System (FCS) Model

The boundary completion mechanism outlined above can be used to
account for both the Kanizsa type illusions as shown above, and the
perceptual grouping phenomena shown below, because in all these cases
the illusory boundary or grouping percept completes a collinear
relation between spatially separated inducers. There is however a
significant difference between these percepts, specifically, that in
the Kanizsa illusions the illusory contour exhibits an actual
brightness contrast across the illusory edge, whereas in the
perceptual grouping phenomena all that is perceived is an invisible
grouping relation.
Grossberg proposes a solution to this problem by suggesting that the
perceptual system consists of two distinct but interacting mechanisms,
the Boundary Contour System (BCS), which represents only the invisible
grouping percept, and the Feature Contour System (FCS), which
represents the visible brightness percept. The figure below shows a
simplified schematic of the BCS / FCS interaction for the case of an
original image, labeled ORIG in the figure, consisting of a white
square on a black background. A plot of image intensity along a
horizontal scan line through the center of the image is shown below
the image. The retinal response to this input can be modeled
approximately by an on-center off-surround receptive field filtering,
as shown schematically in the figure, labeled DOC, where a light color
represents a positive response, a dark color a negative response, and
the neutral gray indicates a zero response. The scan line plot below
the DOC image shows how this representation preserves the direction of
contrast across the edge while showing no signal in the uniform dark
or light regions. In the BCS these edge signals are abstracted to a
contrast-insensitive edge representation, so that the dark/light edge
at the left side of the square and the light/dark edge at the right
side of the square both produce an equal positive response in the BCS
image, as shown in the figure. The BCS signal therefore represents
the edge information in the original, independent of direction of
contrast. It is within this contrast-insensitive representation that
boundary completion in the BCS or in the Directed Diffusion model are
performed, as described above.
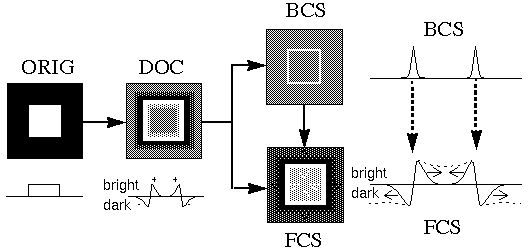
In the FCS representation, initially the signal is identical to the
DOC image, but the nature of the FCS is a
diffusion
operation that allows the brightness and darkness signals to diffuse
spatially across the image, except where gated by the presence of a
BCS signal. This is indicated in the enlarged scan line plots to the
right in the figure above, where the BCS plot exhibits two peaks along
the vertical edges of the square, exactly between the dark and bright
peaks of the FCS image. The brightness signal is free to diffuse
inwards, and the darkness signal is free to diffuse outward,
eventually filling the inner square with a uniform bright percept, and
the outer background with a uniform dark percept, but the presence of
the BCS edge along the perimeter of the square prevents the brightness
and darkness signals from mixing across that line. The final percept
at equilibrium therefore is an approximate reconstruction of the
original image, as indicated by the dotted lines in the FCS scan line
plot.
In the simple example presented in this case, the result of all this
complex processing is simply a decomposition followed by a
reconstruction of the original image. There are several interesting
functions that are served by this BCS / FCS interaction. In the first
place, the retinal on-center off-surround filtering has the effect of
"discounting the illuminant", i.e. the global illumination value is
lost, but the relative illumination at the edges is preserved, so that
the reconstructed FCS image is actually insensitive to absolute
illumination and represents a spatial percept based on only relative
illumination. Land [] has shown that this is indeed a property of
human color and brightness perception, and is the reason for the
brightness contrast effect
which is reproduced by the BCS / FCS model. Another important
property of this model is that it accounts for the blind spot
illusion, the fact that the retinal blind spot is not perceived as a
perceptual hole, or missing information, but rather it takes on the
brightness percept of the surrounding region. Visual stabilization
experiments by Yarbus [ ] exhibit similar phenomena which are also
explained by the BCS / FCS model.
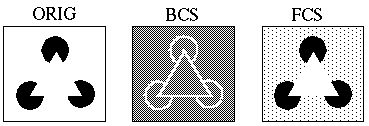
The figure above shows schematically how the BCS / FCS model explains
the Kanizsa illusion. The boundary completion operation of the BCS
generates the missing sides of the triangle, but without the FCS this
would result in only an invisible grouping percept. The influence of
the BCS on the FCS signal however creates an enclosed boundary around
the perimeter of the triangle which then captures a disproportionate
concentration of the diffusing brightness signal due to the high
contrast at the corners, resulting in the perception of a brighter
triangle over a less bright background. In the case of the invisible
grouping percepts shown near the top of this page there is no such
imbalance in brightness signal, and therefore the percept is
represented only in the BCS system, and thus remains
invisible, although not imperceptible.
One of the greatest contributions of the BCS / FCS model is the
introduction of this distinction between the visible and invisible, or
boundary and surface components of perception, both of which clearly
represent manifestations of
[reification]
as opposed to abstraction from the original image.
Return to argument
Return to Steve Lehar




