Plato's Cave: The Lighted Bubble Model
The Lighted Bubble Model
You will recall that in the
[Bubble Model]
the input image is projected on the front face of a block of
perceptual tissue from whence it stimulates the percept of surfaces in
depth within the volume of the block by inverse projection. The
perceived surface is represented by a change in state of the elements
of the block from transparent to opaque, at a depth corresponding to
the depth of the perceived surface.
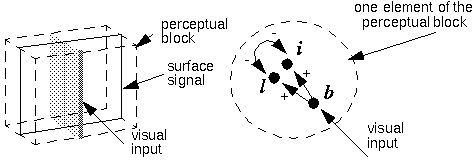
In the lighted bubble model each element of the block encodes
three values; one for the perceived brightness,
b of the surface, one for the underlying
"lightness" l or reflectance of the surface,
and one for the perceived strength of illumination
i of that surface. The perceived brightness
is copied directly from the input image on to the surface, where it is
factored into lightness and illumination by the formula
b = l x i
in other words, the brighter the supposed illumination strength, the
darker the surface reflectance must be to account for the perceived
brightness, and vice-versa. This relationship can be encoded
dynamically by three "nodes" representing the three values; node
b copies its value directly from the input
image, and sends activation to both nodes l
and i in proportion to its own activation.
Nodes l and i have
a mutually inhibitory connection, so the stronger the activation of
one of them, the more it weakens the other. This circuit encodes the
factorization of brightness into lightness and illuminance for every
point on the perceived surface.
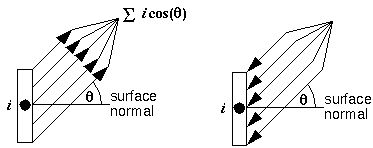
The illuminance value of a surface gives information about the
strength and direction of the illumination source- the brighter the
source, and the more normal its direction of illumination to the
surface, the greater the illumination of that surface. This
information can therefore be "projected backwards" as a hypothesis of
the illumination source, using the "texture of collinearity
connections" by providing a "cosine gating" between the illuminance
node i and all collinearity lines passing
through that point, i.e. the activation value of node
i is projected backwards at full strength in
a direction normal to the perceived surface, and at the reduced
strength of i cos(theta) at angles
theta deviating from normal.
Each point on the surface of the perceptual sphere would summate all
of the cosine gated illuminances from all surfaces projected backwards
in the direction represented by that point. The surface of the
perceptual sphere would thereby reflect an approximation of the
illumination profile of the perceived scene. If many surfaces exhibit
a bright "sunny side" in a certain direction, this would be reflected
as a bright cosine function on the surface of the sphere, centered at
that direction.
The illuminance strength on the surface of the perceptual sphere in
turn is projected backwards to all opaque surfaces in the whole
representation to impinge on those surfaces again through a
cosine-gated connection, so that an illuminant from a certain
direction would light up surfaces facing that direction in a manner
that mimmicks the physics of light falling on a surface. This
illuminant signal is communicated again to the local illuminance node
i at every point in every perceived surface.
This feedback connection expresses the relation that if most surfaces
facing a certain direction reflect strong illumination, that suggests
a strong illumination source in that direction. Conversely, if there
is a strong illumination source in a certain direction, then all
surfaces facing that direction would be expected to have a high
illumination value. If a surface facing in that direction exhibits a
low brightness, then this is likely due to a low
reflectance of that surface, rather than low illuminance.
This latter statement is embodied in the competitive relationship
between nodes l and
i, because l would
be held at a high value due to the feedback from the "illumination
source", which combined with a low value of the perceived brightness
b would result in a low value for the
lightness node l.
One more interaction is required to complete the model, and that is
the tendency (in the absence of contradictory information) for objects
to be perceived as having uniform lightness. This relation is
expressed by the diffusion of lightness signal across perceived
surfaces, so that a lightness value at one point on the surface will
tend to equalize to the lightness value of neighboring points, except
when separated by a perceived lightness edge. A visible edge in an
image that is perceived as a form edge therefore would
not restrict this diffusion of lightness, and thereby would
attempt to account for any brightness difference across that edge by a
difference in illuminance across that edge. This diffusion of
lightness information corresponds to the diffusion of brightness in
Grossberg's
[Feature Contour System]
model.
Return to argument
Return to Steve Lehar


