Plato's Cave: Orientational Harmonic Model
The Orientational Harmonic Model
An extension to the
[Directed Diffusion model],
the Orientational Harmonic model [Lehar 1994] accounts for all of the
illusory vertex phenomena discussed above, and many more by way of a
single simple mechanism. This model proposes that the cells in the
cooperative layer representing different orientations at a single
spatial location are arranged in rings, as shown below, the cell at
three o'clock representing a horizontal edge to the right, nine
o'clock a horizontal edge to the left, twelve o'clock a vertical edge
above, etc.
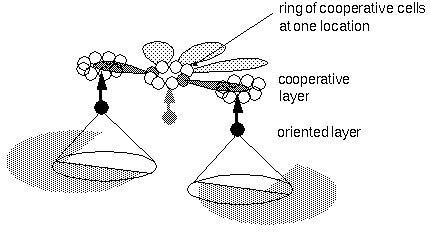
This arrangement is consistent with the pinwheel model of cortical
organization proposed by Braitenberg [2]. Each cell in the cooperative
ring receives oriented input directly from the corresponding oriented
cell at the same location, as well as indirectly from neighboring
regions of the cooperative layer by way of monopolar receptive fields
which receive oriented activation from like-oriented cooperative cells
at adjacent locations in the oriented direction. For example the cell
at three o'clock receives activation directly from the horizontal
oriented cell at the same location (suggested by the shaded oriented
cell in the figure) and indirectly from horizontal oriented cells
displaced in the three o'clock direction by way of a cooperative
receptive field which receives cooperative activation from that
direction.
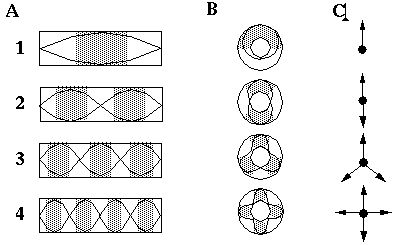
According to the Orientational Harmonic model, the cells in the
cooperative ring are coupled so as to support standing waves of
circular harmonic resonance within the cooperative ring. Harmonic
resonance, whether mechanical, acoustical, or electrical, is a
fundamental property of all physical systems, and has the property of
sub-dividing the resonating system into integer numbers of equal
intervals of alternating active and inactive regions. For example
A in the figure below illustrates the first four
harmonics of acoustical vibration in a linear tube, like a flute,
where the grey shading denotes regions of high amplitude oscillation.
C illustrates the first four harmonics of oscillation
in a circular resonant system, like a closed circular tube. In an
orientational representation such as the one proposed by this model,
the patterns of standing waves depicted in B
represent patterns of edges intersecting at a vertex, as shown in
C. For example the fourth harmonic represents a
four-way, or "+" vertex, the third harmonic represents a three-way "Y"
vertex, the second harmonic represents a straight-through or colinear
feature, while the first harmonic represents a single edge which
terminates at the center, or an end-stop feature. There is also a
zeroth harmonic which represents edge signals at all orientations
equally, which is the pattern seen in response to a small circular
dot.
Return to argument
Return to Steve Lehar


