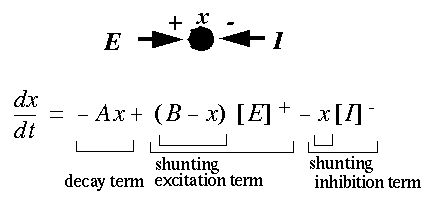
The shunting neuron x can receive both excitatory E and inhibitory I inputs whose values can be any positive quantity.

The excitatory term is "shunted" or bounded by the (B - x) excitatory shunting term which goes to zero as the activation x approaches the maximum value B, while the inhibitory term is "shunted" by multiplication by the inhibitory shunting term, x, which reduces the inhibitory influence to zero as the activation x approaches zero.
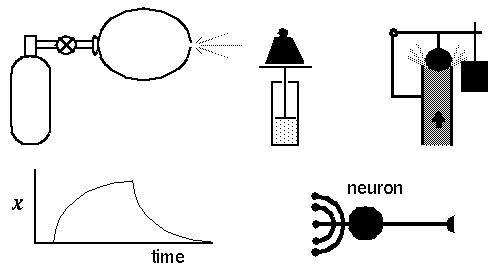
The shunting neuron thus has the property that any increase in excitatory input will increase its activation, but nevertheless its activation remains bounded by the maximum value B. The shunting neuron thus behaves qualitatively like a leaky balloon connected to a gas supply, whose size will asymptotically approach a maximum upon opening of the valve, or asymptotically approach zero upon closing of the valve, (where the leak represents the decay term); or a piston in a closed cylinder whose movement is bounded by the compression of the gas; or like a pressure relief valve whose internal pressure is bounded by the escape of excess gas; or indeed like a neuron, whose maximum activation is bounded by the physical processes governing it.