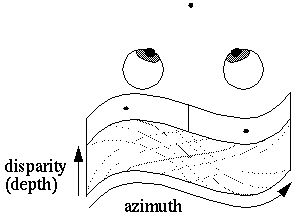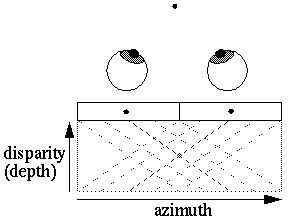

The Projection Field theory has been proposed (revisited by Marr []) whereby the depth information can be recovered by projecting the left and right images through each other at an angle, as shown by the grey lines above, and the depth of any feature is found at the point where the left and right projections of that feature meet. In a neural network model this projection could be performed by a matrix of neural tissue with synaptic connections parallel to the projection lines, so that for example the gray cell depicted at the center of this tissue above receives input specifically from the active cells in the two occular dominance columns.
This matrix of neural tissue therefore is an explicit spatial representation, where one dimension represents the azimuth and the other represents the disparity, or a distorted representation of depth. This kind of representation is what is meant by a fully spatial representation, because the spatial dimensions of the external world are mapped to spatial dimensions in the internal model.
Neurophysiological studies of the visual cortex [] have confirmed the existance of such disparity-specific cells, i.e. cells which respond to a feature at a specific location and disparity in the visual field, which therefore provides evidence for a fully spatial representation at least in the primary visual cortex.
The depth dimension might well be represented at a much lower resolution than azimuth and elevation, and the disparity representation introduces further nonlinearities. Additional distortions corresponding to the irregular folding of the cortex would further distort the physical matrix, as suggested below. Such distorted representations would still comprise a fully spatial system by this definition because the operations of boundary and surface completion can still be performed by a spatial diffusion of neural activation through that matrix.