Plato's Cave: Fully Spatial Representation
The Fully Spatial Representation
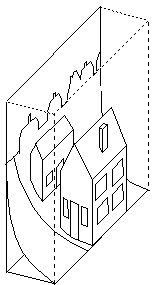
I use the term "fully spatial" in this context to mean a
representation in which spatial extension in the external world is
represented by spatial extension in the internal representation,
although topological distortion is permitted. For example the model
below would be considered a fully spatial model even though
depth is encoded with a vergence representation, i.e. the depth
dimension experiences a highly nonlinear squashing as the distance
represented approaches infinity. Nevertheless, in this
representation, distances are represented by distances, surfaces are
represented by surfaces, and external volumes are represented by
volumes in this internal representation.
There is some
neurophysiological evidence
for this kind of fully spatial representation in the brain, and there
are considerations of
computational complexity
which also support the fully spatial representation.
It might be argued that any computation which can be performed in a
spatial representation could also be performed in a computationally
equivalent non-spatial system, and that therefore this issue of the
fully spatial representation is irrelevant. While this argument is
theoretically correct, the nature of the spatial operations
of collinear and coplanar filling-in are such that a non-spatial
implementation is
computationally implausible,
and therefore the fully spatial model is the only plausible
alternative.
Return to argument
Return to Steve Lehar

