Plato's Cave: Fully Spatial Computation
Computational Issues in the Fully Spatial Representation
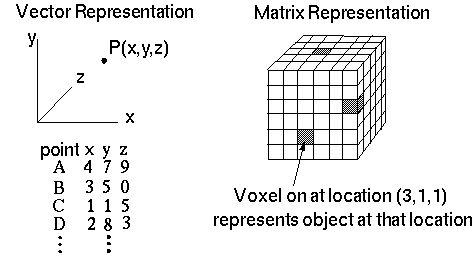
There are two alternative ways to represent space, which can be called
the vector and the matrix representations. In a vector representation,
objects in space are located by their coordinates, for example x, y, z
vectors. Every object must have it's own vector entry, and empty
spaces between objects are not represented. In the matrix
representation the space is represented explicitly by a matrix of
cells, and objects in that space are encoded by a change in state of
those cells. In a matrix representation, the whole space is
represented at all times, whether or not there is anything in that
space.
The dichotomy between these two alternatives is fundamental to the
nature of spatial representation, and can be reduced more generally to
a choice between representing the space itself versus representing the
objects in that space. All spatial representations must consist of
one or another of these two alternatives, or some combination of
them.
It is the nature of the reification operations of boundary completion
and surface filling-in that dictate the choice of a matrix
representation, because these operations perform their filling-in in
empty space, between visual features, and therefore they require an
explicit representation of that empty space. An equivalent
non-spatial algorithm, while theoretically possible, would be
computationally implausible.
Return to argument
Return to Steve Lehar

