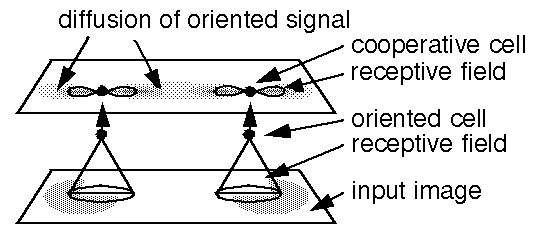
Consider the computation performed by the [Directed Diffusion model], where the presence of a local oriented edge stimulates a local orientation sensitive cell, which in turn propagates activation to adjacent cells in a two-dimensional matrix through a spatial receptive field as suggested below, so as to stimulate neighboring collinearly aligned cells, with the highest activation going to the nearest collinear cells.

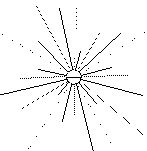
Furthermore, these connections are described by a smooth Gaussian profile which decays with distance from the cell, and with distance from the line of colinearity. A single such receptive field could only be crudely approximated by a large web of long range connections in a non-spatial representation, as suggested above, where each radial line represents a synaptic link corresponding to a single point in the Gaussian projective field, many of which would have to have very small values representing the tails of the Gaussian functions. At every spatial location similar receptive fields would be needed representing every orientation from that location.
Another advantage of the spatial representation is that it can take advantage of the physical properties of neural propagation, turning potential liabilities into assets. For example the high electrical activity of a neuron responding to a strong input may tend to spill over to physically adjacent neurons, resulting in a spatial spread of activation around that point. In the non-spatial representation this would pose a problem unless adjacent neurons and adjacent axons were perfectly isolated electrically. Also, the long range synaptic connections would have to have minimal transmission losses over long distances in order to maintain the fidelity of the projective field profile. In the fully spatial representation on the other hand, neural cross-talk near an active node would simply contribute to the spatial diffusion of oriented activation, and propagation losses with distance would simply smooth out the Gaussian profile of the projective field. Indeed, the Gaussian receptive field of the Directed Diffusion model may actually represent a simple spatial diffusion rather than a physical receptive field. This would not be possible in a non-spatial representation.
While an equivalent non-spatial representation is theoretically possible, practically speaking such an arrangement would present serious implementation problems without offering any advantages, and is therefore highly unlikely. The spatial representation on the other hand can take advantage of the spatial properties of the representation to mimic spatial aspects of the external world.
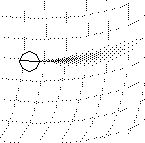
The arguments in support of a spatial representation would apply equally to a representation with topology preserving distortions, because adjacent points in the representation correspond to adjacent points in the external world. The diffusion of oriented activation would have to conform to this geometrical distortion- for example in the regions of the neural structure where the lines representing colinearity follow smooth curves, the diffusion of oriented activation would have to follow those same curves, as suggested below, where the grey lines represent a curved grain of neural texture which ducts the diffusion of activation along the curve of the grain, or influences the growth of the cells' projective fields parallel to the grain.