
The most prominent evidence that the world we see around us is actually inside our heads, comes from an observation on the nature of phenomenal perspective, which anyone can easily verify for themselves. And yet it is an observation which seems to have escaped the attention of the greatest minds who have ever studied the subject of perspective.
Extract from my paper:
Consider the phenomenon of perspective, as seen for example when standing on a long straight road that stretches to the horizon in a straight line in opposite directions. The sides of the road appear to converge to a point both up ahead and back behind, but while converging, they are also perceived to pass to either side of the percipient, and at the same time, the road is perceived to be straight and parallel throughout its entire length. This property of perceived space is so familiar in everyday experience as to seem totally unremarkable. And yet this most prominent violation of Euclidean geometry offers clear evidence for the non-Euclidean nature of perceived space. For the two sides of the road must therefore in some sense be perceived as being bowed, and yet while bowed, they are also perceived as being straight. This can only mean that the space within which we perceive the road to be embedded, must itself be curved. In fact, the observed warping of perceived space is exactly the property that allows the finite representational space to encode an infinite external space. This property is achieved by using a variable representational scale, i.e. the ratio of the physical distance in the perceptual representation relative to the distance in external space that it represents. This scale is observed to vary as a function of distance from the center of our perceived world, such that objects close to the body are encoded at a larger representational scale than objects in the distance, and beyond a certain limiting distance the representational scale, at least in the depth dimension, falls to zero, i.e. objects beyond a certain distance lose all perceptual depth. This is seen for example where the sun and moon and distant mountains appear as if cut out of paper and pasted against the dome of the sky.

The distortion of perceived space is suggested in figure 1 which depicts the perceptual representation for a man walking down a road. The phenomenon of perspective is by definition a transformation defined from a three-dimensional world through a focal point to a two-dimensional surface. The appearence of perspective on the retinal surface therefore is no mystery, and is similar in principle to the image formed by the lens in a camera. What is remarkable in perception is the perspective that is observed not on a two-dimensional surface, but somehow embedded in the three-dimensional space of our perceptual world. Nowhere in the objective world of external reality is there anything that is remotely similar to the phenomenon of perspective as we experience it phenomenologically, where a perspective foreshortening is observed not on a two-dimensional image, but in three dimensions on a solid volumetric object. The appearence of perspective in the three-dimensional world we perceive around us is perhaps the strongest evidence for the internal nature of the world of experience, for it shows that the world that appears to be the source of the light that enters our eye, must actually be downstream of the retina, for it exhibits the traces of perspective distortion imposed by the lens of the eye, although in a completely different form.
This view of perspective offers an explanation for another otherwise paradoxical but familiar property of perceived space whereby more distant objects are perceived to be both smaller, and yet at the same time to be perceived as undiminished in size. This corresponds to the difference in subject's reports depending on whether they are given objective v.s. projective instruction (Coren et al., 1994. p. 500) in how to report their observations, showing that both types of information are available perceptually. This duality in size perception is often described as a cognitive compensation for the foreshortening of perspective, as if the perceptual representation of more distant objects is indeed smaller, but is somehow labeled with the correct size as some kind of symbolic tag representing objective size attached to each object in perception. However this kind of explanation is misleading, for the objective measure of size is not a discrete quantity attached to individual objects, but is more of a continuum, or gradient of difference between objective and projective size, that varies monotonically as a function of distance from the percipient. In other words, this phenomenon is best described as a warping of the space itself within which the objects are represented, so that objects that are warped coherently along with the space in which they are embedded appear undistorted perceptually. The mathematical form of this warping will be discussed in more detail below.
The peculiar properties of phenomenal perspective are explored in the Hallway Experiment.
The phenomenal world is composed of solid volumes, bounded by colored surfaces, embedded in a patial void. Every point on every visible surface is perceived at an explicit spatial location in three-dimensions (Clark 1993), and all of the visible points on a perceived object like a cube or a sphere, or this page, are perceived simultaneously in the form of continuous surfaces in depth. The perception of multiple transparent surfaces, as well as the experience of empty space between the observer and a visible surface, reveals that multiple depth values can be perceived at any spatial location. I propose to model the information in perception as a computational transformation from a two-dimensional colored image, (or two images in the binocular case) to a three-dimensional volumetric data structure in which every point can encode either the experience of transparency, or the experience of a perceived color at that location. The appearence of a color value at some point in this representational manifold corresponds by definition to the subjective experience of that color at the corresponding point in phenomenal space. If we can describe the generation of this volumetric data structure from the two-dimensional retinal image as a computational transformation, we will have quantified the information processing apparent in perception, as a necessary prerequisite to the search for a neurophysiological mechanism that can perform that same transformation.
An explicit volumetric representation of perceived space as proposed here must necessarily be bounded in some way in order to allow a finite representational space to map to the infinity of external space, as suggested in figure 1. The nonlinear compression of the depth dimension observed in phenomenal space can be modeled mathematically with a vergence measure, which maps the infinity of Euclidean distance into a finite bounded range, as suggested in figure 2 A.This produces a representation reminiscent of museum diaramas, like the one depicted in figure 2 B, where objects in the foreground are represented in full depth, but the depth dimension gets increasingly compressed with distance from the viewer, eventually collapsing into a flat plane corresponding to the background. This vergence measure is presented here merely as a nonlinear compression of depth in a monocular spatial representation, as opposed to a real vergence value measured in a binocular system, although this system could of course serve both purposes in biological vision. Assuming unit separation between the eyes in a binocular system, this compression is defined by the equation
[ Note for HTML version: If your browser does not load the "Symbol" font, the greek letters will not appear correctly in the text, Pi appears as p, theta appears as q, sigma appears as s etc. If you see proper greek letters here, this problem does not apply to you.]
where n is the vergence measure of depth, and r is the Euclidean range, or distance in depth. Actually, since vergence is large at short range and smaller at long range, it is actually the "p-compliment" vergence measure r that is used in the representation, where r = (p-n), and r ranges from 0 at r = 0, to p at r = infinity.
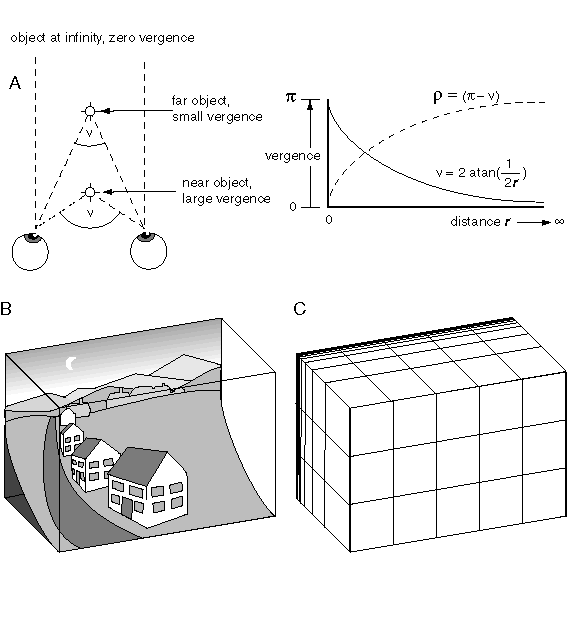
What does this kind of compression mean in an isomorphic representation? If the perceptual frame of reference is compressed along with the objects in that space, then the compression need not be perceptually apparent. Figure 2 C depicts this kind of compressed reference grid. The unequal intervals between adjacent grid lines in depth define intervals that are perceived to be of equal length, so the flattened cubes defined by the distorted grid would appear perceptually as regular cubes, of equal height, breadth, and depth. This compression of the reference grid to match the compression of space would, in a mathematical system with infinite resolution, completely conceal the compression from the percipient. In a real physical implementation there are two effects of this compression that would remain apparent perceptually, due to the fact that the spatial matrix itself would have to have a finite perceptual resolution. The resolution of depth within this space is reduced as a function of depth, and beyond a certain limiting depth, all objects are perceived to be flattened into two dimensions, with zero extent in depth. This phenomenon is observed perceptually, where the sun, moon, and distant mountains appear as if they are pasted against the flat dome of the sky.
The other two dimensions of space can also be bounded by converting the x and y of Euclidean space into azimuth and elevation angles, a and b, producing an angle / angle / vergence representation, as shown in figure 3 A. Mathematically this transformation converts the point P(a,b,r) in polar coordinates to point Q(a,b,r) in this bounded spherical representation. In other words, azimuth and elevation angles are preserved by this transformation while the radial distance in depth r is compressed to the vergence representation r as described above. This spherical coordinate system has the ecological advantage that the space near the body is represented at the highest spatial resolution, whereas the less important more distant parts of space are represented at lower resolution. All depths beyond a certain radial distance are mapped to the surface of the representation which corresponds to perceptual infinity.
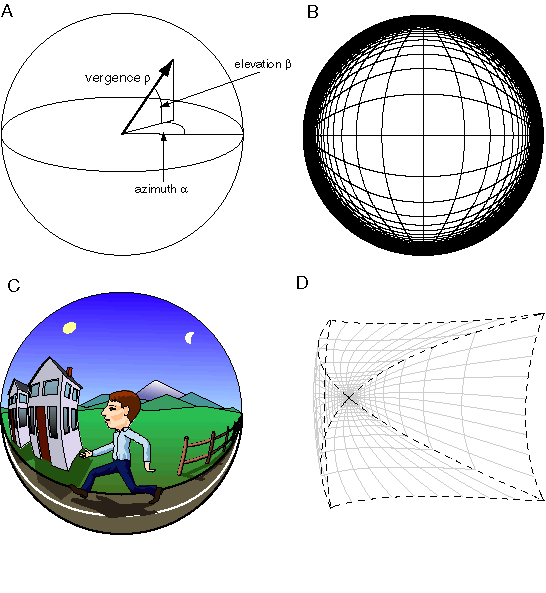
The mathematical form of this distortion is depicted in figure 3 B, where the distorted grid depicts the perceptual representation of an infinite Cartesian grid with horizontal and vertical grid lines spaced at equal intervals. This geometrical transformation from the infinite Cartesian grid actually represents a unique kind of perspective transformation on the Cartesian grid. In other words, the transformed space looks like a perspective view of a Cartesian grid when viewed from inside, with all parallel lines converging to a point in opposite directions. The significance of this observation is that by mapping space into a perspective-distorted grid, the distortion of perspective is removed, in the same way that plotting log data on a log plot removes the logarithmic component of the data. Figure 3 C shows how this space would represent the perceptual experience of a man walking down a road. If the distorted reference grid of figure 3 B is used to measure lines and distances in figure 3 C, the bowed line of the road on which the man is walking is aligned with the bowed reference grid and therefore is perceived to be straight. Therefore the distortion of straight lines into curves in the perceptual representation is not immediately apparent to the percipient, because they are perceived to be straight. However in a global sense there are peculiar distortions that are apparent to the percipient caused by this deformation of Euclidean space. For while the sides of the road are perceived to be parallel, they are also perceived to meet at a point on the horizon. The fact that two lines can be perceived to be both straight and parallel and yet to converge to a point both in front and behind the percipient indicates that our internal representation itself must be curved. The proposed representation of space has exactly this property. Parallel lines do not extend to infinity but meet at a point beyond which they are no longer represented. Likewise the vertical walls of the houses in figure 3 C bow outwards away from the observer, but in doing so they follow the curvature of the reference lines in the grid of figure 3 B, and are therefore perceived as being both straight, and vertical. Since curved lines in this spherical representation represent straight lines in external space, all of the spatial interactions discussed in the previous section, including the coplanar interactions, and collinear creasing of perceived surfaces, must follow the grain or curvature of collinearity defined within this distorted coordinate system. The distance scale encoded in the grid of figure 3 B replaces the regularly spaced Cartesian grid by a nonlinear collapsing grid whose intervals are spaced ever closer as they approach perceptual infinity but nevertheless represent equal intervals in external space. This nonlinear collapsing scale thereby provides an objective measure of distance in the perspective-distorted perceptual world. For example the houses in figure 3 C would be perceived to be approximately the same size and depth, although the farther house is experienced at a lower perceptual resolution.